УМОВИ УТВОРЕННЯ ДИНАМІЧНОЇ МОДЕЛІ

Механізм машинного агрегату звичайно є багатоланковою системою, навантаженою силами і моментами, прикладеними до різних його ланок. Щоб краще уявити собі це, розглянемо, як приклад, механізм подачі заготовок, у якому електродвигун надає рух через зубчасту передачу і кривошип 1 - механізму подачі.

До повзуна 3 прикладена сила корисного (технологічного) опору

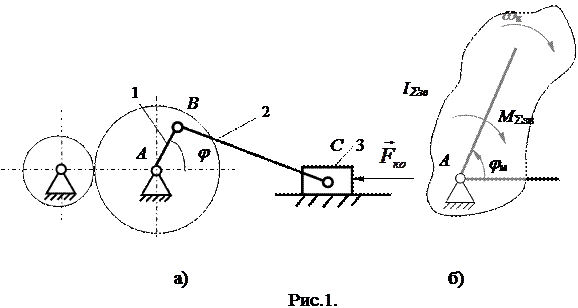Fк.о. (рис.1,а). До ланки 1 прикладений зрівноважувальний (рушійний) момент.

Визначення закону руху такої складної багатоланкової системи являє собою складну задачу. Однак у розглянутому прикладі механізм має один ступінь вільності (w = 1).

Це значить, що насамперед треба визначити закон руху однієї з його ланок, яка буде початковою.

Така постановка задачі приводить до думки, замінити весь складний багатоланковий механізм однією умовною ланкою.

Оберемо як початкову ланку досліджуваного механізму – ланку 1 (кривошип). До умовної ланки (рис 1,б) пред'явимо таку вимогу: нехай її момент інерції і момент, яким вона навантажена, будуть такими, що закон руху умовної ланки вийде цілком співпадаючим із законом початкової ланки 1.

Отже умовна ланка виявиться своєрідною динамічною моделлю механізму. А звідси випливає, що коли визначити закон руху цієї простої моделі (рис.1,б), то автоматично стане відомим шуканий закон руху початкової ланки заданого механізму, тобто для будь-якого моменту часу буде виконуватись рівняння:

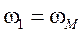(1)

де, w₁ – кутова швидкість початкової ланки (у нашому випадку ланка 1;

w_м – кутова швидкість моделі.

Зі сказаного випливає, що при побудові моделі механізму усі сили і моменти, прикладені до нього, виявляються зведеними до однієї ланки і заміненими сумарним зведеним моментом (узагальнена сила в теоретичній механіці). Так само маси усіх ланок (точніше кажучи, їхні інертності) виявляються також зведеними до однієї ланки і заміненими СУМАРНИМ ЗВЕДЕНИМ МОМЕНТОМ ІНЕРЦІЇ, який є, таким чином, еквівалентом всієї інертності механізму.

Сам же заданий багатоланковий механізм (рис.1,а), навантажений складною системою сил і моментів, виявляється заміненим простою моделлю (рис. 1, б).

Отже, побудова динамічної моделі складається в зведенні сил і в зведенні мас. Виконання рівняння (1) буде забезпечене, але в тому випадку, якщо при зведенні сил буде дотримана умова рівності потужностей, а при зведенні мас - умова рівності кінетичних енергій.

2. ЗВЕДЕННЯ СИЛ.

Розглянемо зведення сил на прикладі механізму з одним ступенем вільності, w = 1, (рис.2, а). Виберемо, як початкову, ланку 1. Механізм навантажений силами Fк.о., Fі, G2 і моментом М_зр. Замінимо механізм його динамічною моделлю і зведемо до неї всі сили і моменти. У результаті сили Fк.о., Fі2, G2 і момент М_зр будуть представлені відповідними зведеними моментами (рис.4,б). Їх алгебраїчна сума дасть величину сумарного зведеного моменту.

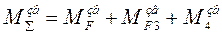(2)

прикладеного до моделі (рис.4,в.)

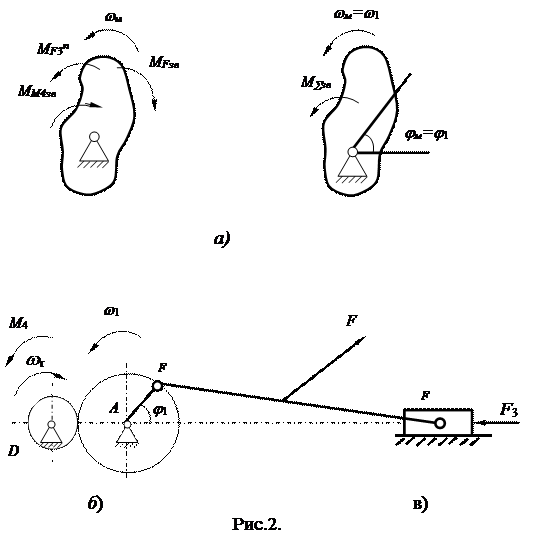
Для визначення зведених сил або моментів використовуємо рівність:

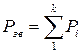(3)

Р_зв – потужність зведеної сили або зведеного моменту.

P_i – потужність, сили або момента прикладених до ланки і

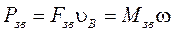(4)

F_зв – величина зведеної до точки В ланки зведення сили (може бути силою рушійною або опору);

Vв – швидкість точки В зведення;

Мзв – зведений момент пари сил (Мр або Мо)

w - кутова швидкість ланки зведення.

Тоді з рівності (13) з урахуванням (12) маємо:

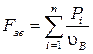(5)

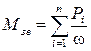(6)

Сумарна потужність, яку створюють всі сили і моменти прикладені до

ланок механізму:

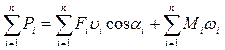(7)

де Fi, Мi – сила і момент прикладені до ланки і;

Vi – швидкість точки прикладення сили F_i;

w_i – кутова швидкість ланки і;

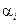– кут, утворений силою F_i і вектором швидкості Vi

Підставляємо вирази (7) у (5), (6)

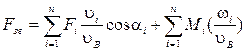(8)

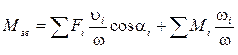(9)

З рівнянь (8), (9) випливає, що якщо для кожного положення механізму відомі прикладені до його ланок сили і моменти, то зведена сила чи зведений момент залежать тільки від співвідношення швидкостей.

За цією методикою визначаються зведені моменти сил рушійних Мр, корисних опорів Мк.о., шкідливих опорів, Мш.о., сил тяжіння М_G

Алгебраїчну суму всіх зведених моментів сил називають над- лишковим (сумарним) моментом:

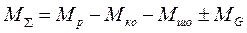(10)

3. КІНЕТИЧНА ЕНЕРГІЯ МЕХАНІЗМУ.

Кінетична енергія ланки, що поступально рухається (рис.3):

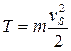(11)

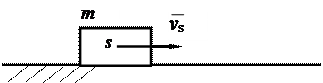
Рис.3.

m - маса ланки;

Vs - швидкість центра мас поступально рухається ланки.

Кінетична енергія ланки що здійснює обертальний рух, коли центр мас збігається з віссю обертання (рис.4):

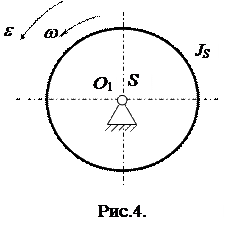
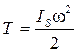(12)

Is – момент інерції ланки відносно вісі, що проходить через центр мас перпендикулярно до площини руху;

w - кутова швидкість ланки.

Кінетична енергія ланки, що здійснює обертальний рух, коли центр мас не збігається з віссю обертання (рис.5).

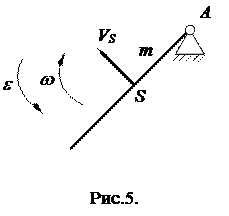Vs - лінійна швидкість центра мас ланки;

Використовуючи теорему Штейнера для однорідної прямолінійної ланки момент інерції ланки відносно осі обертання:

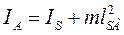(13)

Тоді кінетична енергія ланки:

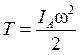(14)

У випадку плоскопаралельного руху ланки його кінетичну енергію можна показати у вигляді суми енергій у поступальному русі разом з центром мас і обертальному русі навколо центра мас:

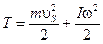(15)

Кінетична енергія всіх ланок машини (без маховика)

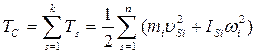(16)

4. ЗВЕДЕНА МАСА І ЗВЕДЕНИЙ МОМЕНТ ІНЕРЦІЇ.

Механізм з одним ступенем вільності (W = 1) має одну початкову ланку, що може бути обрана за ланку зведення, а точку В приймаємо за точку зведення.

Кінетична енергія такого механізму може бути визначена за формулою:

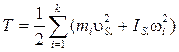(17)

m_i - маса ланки і;

Vsi – швидкість центра мас ланки і;

Isi – момент інерції відносно осі що проходить через центр мас і перпендикулярної площині руху.

w_i – кутова швидкість ланки і.

ЗВЕДЕНОЮ МАСОЮ називають таку умовну масу зосереджену в точці В, кінетична енергія якої дорівнює в кожнім розглянутім положенні механізму сумі кінетичних енергій усіх його ланок. На підставі цього запишемо рівність кінетичних енергій зведеної маси і ланок механізму.

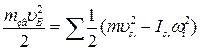(18)

звідки одержуємо формулу для визначення зведеної маси:

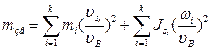(19)

ЗВЕДЕНИЙ до ланки АВ МОМЕНТ ІНЕРЦІЇ МЕХАНІЗМУ - це момент інерції, який повинна мати ланка зведення відносно осі її обертання, щоб кінетична енергія цієї ланки в кожнім розглянутім положенні механізму дорівнювала сумі кінетичних енергій усіх її ланок.

На підставі цього запишемо:

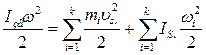, (20)

звідки зведений момент інерції механізму:

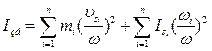(21)

У такий спосіб кінетична енергія механізму може бути визначена одним із двох способів:

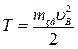(22)

чи

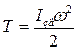(23)

Тоді зведена маса може бути виражена через зведений момент інерції

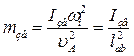(24)

і навпаки, зведений момент інерції через зведену масу:

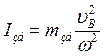(25)

Побудуємо графіки зведених моментів для кривошипно-повзунного механізму показаного на рис.3. Нехай графік сил корисних опорів буде представлений у вигляді графіка F=F(s) (рис.6), де опір робочому ходу визначається F1, а опір холостому ходу у вигляді сили F2. Сила опору робочого ходу F₁ (в межах 180 градусів повороту кривошипа) – постійна.

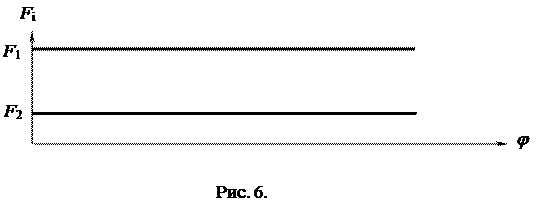Аналогічно сила F2 холостому ходу теж величина постійна.

(26)

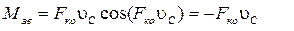Зведений момент для спрощення визначимо тільки від сил корисного опору, скориставшись для цього наступною залежністю:

У цій формулі змінними є значення сил опору та швидкість повзуна. Попередньо визначають швидкість повзуна графічним або аналітичним шляхом. Для кожного положення початкової ланки механізму визначаємо зведений момент за формулою (26) і в відповідному масштабі відкладаємо ординати графіка M_зв (для зручності подальших перетворень від’ємне значення відкладаємо уверх від осі абсцис. Аналогічно будуємо діаграму зведеного момента інерції механізму (рис.7) використовуючи формулу:

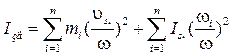(27)

1. РІВНЯННЯ РУХУ МЕХАНІЗМУ.

Виконавши приведення сил і мас, будь-який механізм з одним ступенем вільності, настільки б складним він не був, можна замінити його динамічною моделлю. (рис.1).

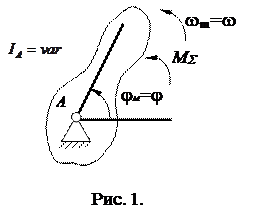Ця модель має в загальному випадку змінний зведений момент інерції і до неї прикладений сумарний зведений момент. Закон руху моделі аналогічний закону руху початкової ланки механізму.

Основою для складання рівняння руху механізму з одним ступенем вільності служить теорема про зміну кінетичної енергії:

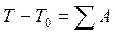. (28)

Роботу виконують всі активні сили і моменти в усіх кінематичних парах механізму.

1. РІВНЯННЯ РУХУ В ЕНЕРГЕТИЧНІЙ ФОРМІ.

Запишемо формулу для кінетичної енергії моделі:

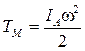. (28)

Оскільки все навантаження, прикладене до моделі, виражається сумарним зведеним моментом, то сума робіт дорівнює

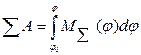. (29)

З огляду на рівність кінетичних енергій динамічної моделі і всього механізму і підставивши вирази (2), (3) в основне рівняння (1), одержимо рівняння руху в енергетичній (інтегральній) формі:

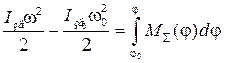. (30)

У загальному випадку верхня межа j інтегрування в рівнянні (30) вважається змінною.

Якщо все навантаження, прикладене до механізму, залежить тільки від його положення, тоді і сумарний зведений момент є функцією лише координати j. У цьому випадку рівняння (30) розв’язується відносно шуканої величини :

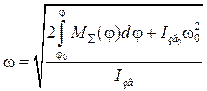. (31)

Вкажемо, що інтеграл під коренем має знак, який треба враховувати.

2. РІВНЯННЯ РУХУ В ДИФЕРЕНЦІАЛЬНІЙ ФОРМІ.

Для виведення рівняння руху в диференціальній формі продиференціюємо рівняння (30) по координаті j:

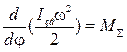. (32)

Визначимо похідну, яка розташована в лівій частині рівняння, пам'ятаючи, що в загальному випадку змінною величиною є не тільки кутова швидкість ланки приведення, але і сумарний зведений момент інерції. Тому

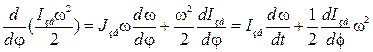, (33)

звідки

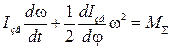. (34)

Це і є рівняння руху в диференціальній формі, оскільки шукана змінна величина - кутова швидкість розташована під знаком похідної. При користуванні рівнянням (34) треба пам'ятати, що сумарний зведений момент, а також похідна – величини алгебраїчні і підставляються зі своїми знаками.

У випадку, коли досліджуваний механізм, що має J_зв = const (наприклад, зубчастий механізм із круглими колесами), тоді рівняння його руху спрощується і має такий вид:

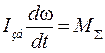. (35)

Для визначення кутового прискорення початкової ланки використовуємо рівняння (34) :

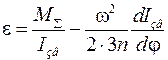. (36)

Величини Må і dJ_зв/dj підставляються в рівняння (10) зі своїми знаками. Якщо кутове прискорення вийде зі знаком, протилежним знаку кутової швидкості, то це значить, що початкова ланка механізму рухається уповільнено.

Похідна dJ_зв/dj підраховується або чисельним диференціюванням на ЕОМ, чи графічно.