Основные законы и формулы, описывающие цепи трёхфазного переменного тока

Приведём важнейшие законы из теории общей электротехники, касающиеся принципов работы электрооборудования на трёхфазном переменном токе.

Синусоидальные токи и напряжения можно представлять как в виде мгновенных величин, так и в виде действующих.

Мгновенные токи и напряжения описывают изменение физической величины в каждый момент времени и обозначаются малыми буквами i, u.

Синусоидальный ток зависит от времени t по формуле:

i(t) = i_maxsin(ωt + φ_i),

где i_max – амплитуда синусоиды тока;

ω – угловая частота;

φ_i – начальная фаза.

Угловая частота определяется по формуле:

ω = 2π f,

где f – частота переменного тока.

Если принять f = 50 Гц, то ω = 314 рад/с.

Аналогично определяется мгновенное напряжение:

u(t) = u_maxsin(ωt + φ_u),

Тепловое действие тока, а также механическая сила взаимодействия двух проводников, по которым проходит один и тот же ток, пропорциональны квадрату тока. Поэтому о величине тока можно судить по его среднеквадратичному значению за период, то есть по действующему значению. В этом случае применяют большую букву I. Действующее значение синусоидального тока численно равно такому постоянному току, который за период выделяет такое же количество тепла, что и синусоидальный ток. Аналогично вводится понятие действующего напряжения U. Действующее значение в 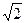раз меньше амплитудного.

Для удобства математического обращения с синусоидальными величинами токов и напряжений, их представляют в виде вращающихся векторов на комплексной плоскости. Так, например, симметричная трёхфазная система токов может быть представлена графически в виде тройки векторов, имеющих одинаковые длины и рассоложенных под углами 120° друг относительно друга – рис. 1.2.

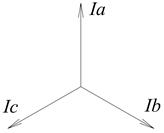
Рис. 1.2. Изображение симметричной трёхфазной системы токов в виде векторов на плоскости

Такое представление позволяет графически складывать и вычитать токи и напряжения, анализировать сдвиг фаз между ними.

Для трёхфазной системы напряжений вводятся понятия фазного и линейного напряжения. Фазное напряжение U_ф – это разность потенциалов между фазой и «землёй» (то есть точкой нулевого потенциала). Линейное напряжение U_л – это разность потенциалов между двумя фазами. На рис. 1.3 показано графическое отображение фазных и линейных напряжений. Пользуясь тригонометрией, несложно доказать, что линейное напряжение в 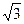раз больше фазного. Так, например, для сетей жилых зданий линейное напряжение составляет 380 В, а фазное 380/корень3 ≈ 220 В.

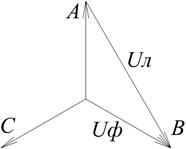
Рис. 1.3. К понятию фазного и линейного напряжения

Закон Ома связывает напряжение U, ток I и полное сопротивление цепи Z:

U = I ∙ Z.

Полное сопротивление цепи состоит из активной R и реактивной Х составляющих:

Z = .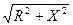

Геометрически данное выражение можно представить в виде треугольника сопротивлений на рис. 1.4. Угол φ между активной и полной составляющей определяет разность фаз между синусоидами тока и напряжения. Косинус этого угла называется коэффициентом мощности и имеет очень важное значение для экономичности работы сети. При φ = 0 сопротивление цепи имеет число активный характер, а ток и напряжение совпадают по фазе.

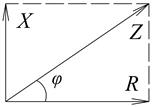
Рис. 1.4. Треугольник сопротивлений

Активное сопротивление определяется удельным сопротивлением проводника ρ, его длиной l и площадью поперечного сечения s по формуле:

R = ρ∙ l / s.

Реактивное сопротивление Х может быть индуктивным (положительным) и емкостным (отрицательным).

Индуктивное сопротивление катушки с индуктивностью L зависит от угловой частоты тока ω прямо пропорционально:

Х_L = ω L.

Если сопротивление цепи чисто индуктивное, то синусоида тока отстаёт от синусоиды напряжения по фазе на 90° (φ = + 90°).

Емкостное сопротивление конденсатора с ёмкостью С зависит от угловой частоты тока ω обратно пропорционально:

Х_С = 1 / ω С.

Если сопротивление цепи чисто емкостное, то синусоида тока опережает синусоиду напряжения по фазе на 90° (φ = – 90°).

Суммарное реактивное сопротивление складывается из сопротивлений Х_L и Х_С с учётом их знаков:

Х = Х_L – Х_С.

Закон электромагнитной индукции Фарадея описывает возникновение ЭДС в рамке при изменении магнитного потока. Фактически данный закон описывает принцип действия простейшего генератора переменного тока. Закон гласит: если внутри рамки изменять магнитный поток Ф, то на концах рамки возникнет ЭДС индукции ε_i, прямо пропорциональная скорости изменения магнитного потока dФ/dt и числу витков рамки N:

ε_i = – N dФ/dt,

где знак минус описывается правилом Ленца: индукционный ток, возникающий при изменении внешнего магнитного потока, имеет такое направление, что его собственный магнитный поток компенсирует изменение внешнего магнитного потока, вызвавшего этот ток.

Важное значение в электротехнике имеет закон, описывающий взаимодействие проводника с током и магнитного поля. При помещении проводника длиной l с током I в магнитное поле с индукцией В, на данный проводник действует сила Ампера:

F_А = В∙I∙l∙sinα,

где α – угол между векторами тока и магнитной индукции.

Направление силы Ампера определяется по правилу левой руки: линии магнитного поля входят в ладонь, четыре пальца указывают направление тока, отставленный большой палец указывает направление силы Ампера. Данный закон описывает принцип действия любого электродвигателя.

Закон Джоуля-Ленца оговаривает тепловое действие тока. Если через проводник сопротивлением R в течение времени t пропускать ток I, то в данном проводнике будет выделяться теплота количеством:

Q = I²∙R∙t.

Квадратичный характер тепловых потерь вынуждает при одной и той же мощности снижать ток за счёт увеличения напряжения, что активно используется в современной энергетике.