Запись команды выбора (case) (уточнение таблицы ситуаций) с помощью набора команд ветвления
Если одна ситуация от другой отличается гораздо больше, чем набором значений одной переменной и когда число ситуаций >2, то нужно записать команду выбора с помощью набора команд ветвления (if). Это можно сделать двумя очень похожими путями:
1) Когда каждая ситуация анализируется (наступила или нет) независимо от наступления или не наступления другой (так надо лишь в случае независимых ситуаций, но можно и для зависимых)
2) Когда мы анализируем (наступила или нет) каждую ситуацию, учитывая результат анализа предыдущих (по порядку анализа) ситуаций.
Рассмотрим пример:
| Ситуация | Действие |
| С1 | D1 |
| C2 | D2 |
| C3 | D3 |
| … … | |
| Cn | Dn |
Выбрать
при С1: D1;
при C2: D2;
при C3: D3;
...
при Cn: Dn;
все.
Для этой команды выбора запишем набор команд ветвления двумя способами.
1-й способ
| Если С1 то D1; все Если С2 то D2; все Если С3 то D3; все ... Если Сn то Dn; все | if (C1) then D1; if (C2) then D2; if (C3) then D3; … if (Cn) then Dn; |
2-й способ (считаем, что ситуации являются зависимыми и наступить может лишь одна из них)
| Если С1 то D1 иначе если С2 то D2 иначе если С3 то D3 иначе .... .................................... если Сn-1 то Dn-1 иначе Dn все все все все | if C1 then D1 else if C2 then D2 else if C3 then D3 else … ................................... if Cn-1 then Dn-1 else Dn; |
В принципе, оба этих способа делают одно и то же. Однако каждый из них требует разных объемов сравнений (число сравнений и там и там одинаково и равно (n-1)). Различаться по объему сравнений эти способы будут в том случае, если ситуации С1, С2, ..., Сn имеют общий признак.
13.6 Запись последовательных команд ветвления в случае, когда соседние зависимые ситуации имеют общие признаки.
Классический пример: вычисление функций на разных интервалах.
Пример: пусть выражение для вычисления функции имеет следующий вид:
f1(x) при x <= -1
y = f2(x) при -1 < x <= 1
f3(x) при 1 < x <= 3
f4(x) при x > 3
x1, x2, x3, ... – границы интервалов определения функции
Для решения поставленной задачи можно использовать нисходящий и восходящий подходы.
Восходящий подход
При вычислении значений функции мы столкнемся со следующими ситуациями:
| Ситуации | Действия | |
| Вычислить y = f1(x) | |
| С2 = x ' (- 1; 1] | Вычислить y = f2(x) | |
| С3 = x ' (1; 3] | Вычислить y = f3(x) | |
| С4 = x ' (3; ¥) | Вычислить y = f4(x) |
Для этой таблицы ситуаций запишем набор команд ветвления. Таких команд ветвления в общем случае будет столько, сколько интервалов имеет функция.
По 1-му сособу записи последовательности операторов if:
if (х > -¥) и (х <= -1)
then вычислить y = f1(x);
| Всегда имеют место |
then вычислить y = f2(x);
if (х > 1) и (х <= 3)
then вычислить y = f3(x);
if (х > 3) и (х < ¥)
then вычислить y = f4(x);
Дальнейшие действия:
1) Из описания ситуации нужно выкинуть избыточные признаки (они всегда имеют место).
2) Внимательно рассмотренная последовательность команд показывает, что при той последовательности анализа цепочки ситуаций одни и те же признаки мы неоднократно проверяем.
При проверке х <= -1 и х > -1 проверяется один и тот же признак: "как соотносятся (х) и (-1)?" просто этот признак имеет разное значение на разных интервалах.
Правило: Если обнаружится, что ситуации имеют общий признак, то необходимо основную форму записи этого признака сделать базовой, а остальные вхождения этого признака выразить через базовую форму (обычно через операцию отрицания, это позволяет использовать результаты проверки предыдущей ситуации при анализе текущей, если операторы if - вложенные).
| NB: Здесь общие признаки есть потому, что смежные интервалы имеют общие границы (левую для одного и правую для другого). |
П1 не П1
x <= 1 x > 1
П2 не П2
Если удалось выявить в ситуации общие признаки и удалось выразить одни признаки через другие, то имеется возможность, при правильном порядке анализа ситуаций (имеющих общие признаки), сократить описание каждой ситуации с двух до одного признака. Правильным порядком в данном случае является порядок, при котором каждая последующая ситуация имеет общий признак с предыдущей. Рассмотрим, как это можно сделать 2-м способом записи команды ветвления (для указанного выше рисунка):
if x <= -1
then вычислить y = f1(x)
else
if x < 1 {уже известно, что x>-1}
then вычислить y = f2(x)
else
if x < 3
then вычислить y = f3(x)
else вычислить y = f4(x);
Здесь при анализе признака x < 1 уже известно, что x > -1. Поэтому проверка ((x > -1) и (x <=1 )) - была бы лишней.
Легко заметить, что объем вычислений (или количество проверок) при этом подходе гораздо меньше.
Нисходящий подход
Выделенные нами ситуации образуют некоторое пространство. Две ситуации С1 и С2 в этом пространстве назовем соседними, если для одной из них обязательным является наличие признака П1, а для другой - его отсутствие:
| С1 С2 |
П1 П2 П3
>
П1 не П1 С1 С2 С3 С4
Мы будем использовать метод половинного деления цепочки ситуаций. Чтобы уменьшить число этапов уточнения надо весь анализируемый интервал делить по числу границ приблизительно пополам. В этом случае на каждом этапе уточнения надо анализировать 2 ситуации: а) попали в левую половину промежутка б) попали в правую половину промежутка. После этого и левую и правую половины интервала надо снова поделить пополам и.т.д.
Пi = ( x 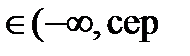 i) )
i) )
Левая половина цепочки Правая половина цепочки
Поскольку здесь выбор идет из двух ситуаций, то их анализ лучше проводить с использованием команд ветвления, а саму разработку алгоритма лучше вести графическим методом: прямо по графику функции (в соответствии с расположением интервалов друг относительно друга) составляем схему алгоритма:
y=f1(x) y=f2(x) y=f3(x) y=f4(x)` y=f5(x) y=f6(x)
x1 x2 x3 x4 x5
14.Циклы с неизвестным числом повторений
В тех циклах, которые мы рассматривали до этого, имелся т.н. параметр цикла, который выполнял следующие функции:
1) С его помощью задавалось нужное количество повторений тела цикла.
2) Выполнение цикла начиналось с нужной компоненты.
3) С его помощью выполнялся переход к нужным данным (следующей компоненте) на очередном повторении цикла.
В циклах с неизвестным числом повторений параметр цикла отсутствует. Для этих циклов необходимо "вручную" выполнить следующее:
1) Необходимо позаботиться, чтобы действия начались с нужной компоненты:
- с нужного слагаемого при нахождении суммы;
- с нужного элемента массива, при обработке массива.
2) Надо позаботиться, чтобы на следующем выполнении (повторении) тела цикла использовались новые данные (следующая компонента).
3) Надо позаботиться, чтобы цикл выполнялся нужное число раз.
Существует две разновидности циклов с неизвестным числом повторений на псевдокоде и Паскале:
Псевдокод:
оператор Паскаль: while ситуация1 do оператор |
| Псевдокод: повторить операторы ; пока не ситуация2; Паскаль: repeat операторы ; until ситуация2; |
| Цикл с постусловием. Он выполняется всегда хотя бы 1 раз. Цикл с постусловием будет выполняться до тех пор, пока ситуация2 не наступит. Эту ситуацию называют ситуацией завершения. |
логическая переменная или лог. выражение
Тело цикла для цикла с предусловием может состоять только из одного оператора. Для цикла с постусловием тело может состоять из нескольких операторов.
В общем случае структура цикла с неизвестным числом повторений имеет следующий вид:
| Цикл с предусловием: {подготовка цикла} Установить нач значение результата Встать на нужный (1-й) компонент нач пока продолжать повтор повторение нц выполнить очередную итерацию кон перейти к следующей компоненте кц тело цикла | Цикл с постусловием: {подготовка цикла} Установить нач. значение результата Встать на нужный (1-й) компонент повторить выполнить очередную итерацию перейти к следующей компоненте пока не завершить; |
С помощью команды ветвления цикл с неизвестным числом повторений можно изобразить следующим образом:
| цикл с предусловием: < подготовка цикла> цикл: если продолжить то нц тело цикла идти к цикл кц всё | цикл с постусловием: < подготовка цикла> цикл: тело цикла если закончить то идти к финиш иначе идти к цикл все финиш: |
| | |
Общей чертой этих двух циклов является наличие проверки, по результатом которых делается вывод о необходимости завершения или продолжения цикла. Поэтому в обоих этих циклах в теле цикла должно содержаться действие, которое влияет на результат этой проверки. Либо в потоке обрабатываемых входных данных должно встретиться значение, завершающее цикл. Если это правило нарушить, то цикл или может ни разу не выполниться, или может выполняться бесконечно.
Циклы, которые не будут выполняться: Примеры простых бесконечных пустых циклов:
While (false) do; - ни разу while true do
Repeat while true; - только один раз. repeat until false;
Рассмотрим простые правильные примеры (шаблоны) использования циклов с неизвестным числом повторений:
1. Цикл, управляемый счетчиком (аналог цикла for, но с произвольным шагом счетчика)
{подготовка цикла}
Счетчик:=0; // инициализация счетчика
while Счетчик <= Конечное_значение do
begin
... проверка счетчика
<Использование текущего значения счетчика>
Счетчик := Счетчик + Шаг; //модификация счетчика (увеличение или уменьшение)
end;
2. цикл, управляемый т.н. «сигнальной меткой»
Используется при обработке потока входных данных, количество которых заранее неизвестно (такие потоки входных данных называются последовательностями).
Последовательность имеет следующие черты:
- число элементов неизвестно;
- последним элементов должен быть признак конца последовательности;
- признак конца последовательности не должен совпадать ни с одним из значащих элементов последовательности;
- нельзя напрямую обратиться к нужному элементу (по имени, по номеру);
- не обязательно хранить в памяти всю последовательность (достаточно хранить только один - текущий для его обработки).
Сигнальная метка (признак конца последовательности) – уникальное значение во входном потоке, которое обозначает конец входного потока, но само это значение не является частью потока - не может использоваться (обрабатываться) как данные. Например, если вводится и обрабатывается поток целых положительных чисел, то в качестве такой сигнальной метки можно принять число = -1. Начинать обработку любой последовательности надо с выбора значения «сигнальной метки» (исходя из типа элементов последовательности).
{подготовка цикла} исходя из типа элементов последовательности
Сигнальная_метка := Выбранное_значение
Считать текущее значение из входного потока и присвоить его входной_переменной
while входная_переменная ≠ Сигнальная_метка do
begin
Обработать текущее значение входной_переменной
Считать текущее значение из входного потока и присвоить его входной_переменной
end;
3. цикл, управляемый событием (флагом)
| Чтобы не было зацикливания, следует делать следующее (при отладке): - считать число шагов (и прерывать цикл, когда число шагов превышает некое максимальное, заранее заданное); - считать время (и прерывать цикл, когда время превышает некое максимальное, заранее заданное). |
{подготовка цикла} или Флаг = false
флаг := False; // инициализация флага
while (Not флаг) do
begin непрерывно гоняя цикл
...
<пусто> если ожидаем наступление внешнего события
или по отношению к программе (процессу)
<выполнение действий, влияющих на флаг>
end;
Рассмотрим более сложный пример:
На интервале [x1, x2] находится корень уравнения. надо найти этот корень.
| NB: Пусть нам известно, что на интервале [x1,x2] существует лишь один корень. Иначе мы найдем лишь один корень из нескольких имеющихся |
x1=A x0 x2=B
f(x0) = 0
Первую формулировку решения можно сразу записать следующим образом:
вычислить корень
При уточнении решения этой задачи возможны 2 ситуации: корень существует и корень не существует.
| Ситуация | Действие |
| корень существует | найти корень |
| корень не существует | сообщить об ошибке и закончить |
Искать корень будем приближенным методом, поэтому чтобы найти корень, придется последовательно решить следующие подзадачи:
найти 1-е приближение
найти 2-е приближение можно свернуть в цикл (число повт. неизвестно заранее)
найти 3-е приближение
...
В общем случае имеем большое количество однотипных действий. Такой линейный алгоритм желательно сворачивать в цикл. Число повторений заранее неизвестно. В данном методе для определения момента остановки задается достигнутая (на текущем шаге) точность поиска корня.
Структура цикла будет иметь вид:
{подготовка цикла} // подготовка нужна, так как в теле цикла используется рекурсия
установить начальное значение корня //найти 0-е приближение;
while продолжать do текущая левая граница
begin текущая правая граница
найти очередное приближение корня | х1 - х2| > e
end заданная точность
Ситуацию "продолжать" можно описать следующим образом: | х1 - х2| > e. Для поиска корня будем использовать метод половинного деления. Суть этого метода поиска корня (метод деления пополам) заключается в следующем: на каждой итерации интервал определения корняделится пополам и определяется середина интервала, т.е. точка x = (х1+х2)/2 . Далее определяется, какую половину интервала выбрать в качестве нового интервала определения корня. На следующей итерации выбранный интервал вновь делиться пополам. При каждом делении интервала текущие значения х1 и х2 как бы приближаются друг к другу. При бесконечном числе повторений х1 и х2 сольются в одну точку (с точностью до e).
Команду "найти очередное приближение" можно разбить на две:
1) выбрать нужную половину интервала (изменить левую или правую границу)
2) вычислить новое значение корня.
Команду "установить начальные значения" можно уточнить таким образом :
Вычислить х:= (x1+x2)/2.
Команда "вычислить новое значение корня" уточняется таким же образом:
вычислить х:= (x1+x2)/2.
Чтобы уточнить задачу «выбрать нужную половину интервала» надо следовать следующим правилам корректировки: в качестве нового интервала выбирается та половина начального интервала., на границе которой функция имеет разные знаки (если функция имеет разные знаки на границах, то это значит, что она через "0" перейдет). В данном случае в качестве нового интервала примем правую половину интервала (функция на границах правой половины имеет разные знаки).
Возможны две ситуации при уточнении команды "скорректировать границы":
| Ситуация | Действие |
| Знаки на интервале [х1; (х1+х2)/2] (левая половина) разные | Принять х2 := (х1+х2)/2 |
| Знаки на интервале [(х1+х2)/2; х2] (правая половина) разные | Принять х1 := (х1+х2)/2 |
Эти ситуации взаимоисключающие, поэтому анализировать (проверять) будем только одну из них.
В итоге уточнения цикла while получим:
Проверка: корень существует? ситуация «продолжать»
{подготовка цикла}
{установить начальное значение корня}
х:= (х1+х2)/2;
while (abs(x1 + x2)> eps) do
begin
{определение новой половины интервала}
if (f(x1) * f((x1 - x2)/2) < 0)
then
{корень в левой половине}
x2:= (x1 + x2)/2
else
{корень в правой половине}
x1:= (x1 + x2)/2;
{определение текущего значения корня на новом интервале}
x:= (x1 + x2)/2;
end;
Дата добавления: 2016-05-28; просмотров: 2955;











