Уточнение многоместных (n - арных) операций
S = 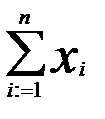 =x1+x2+x3+...+xn
=x1+x2+x3+...+xn
 S=U1 * U2 * U3 * ... * Un S =
S=U1 * U2 * U3 * ... * Un S = 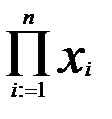 = x1∙x2∙x3∙...∙xn
= x1∙x2∙x3∙...∙xn
обобщенный вид S = XN= x∙x∙x∙...∙x
n – арной операции N раз
S = X!=1∙2∙3∙4∙...∙X
* - так обозначается обобщенная бинарная (двухместная) операция ("+","-",".",":","возведение в степень"). Исполнитель алгоритма, на которого ориентирована программа, к сожалению многоместные операции выполнять не может (имеет только одно вычислительное устройство) и поэтому вычисление многоместных операций нужно заменять на последовательность бинарных операций.
Для решения поставленной задачи (замены многоместной операции последовательностью 2-местных) составим соответствующий линейный алгоритм:
S1=U1 Можно заметить, что строки, начиная со второй, можно записать
S2=S1 * U2 в следующей обобщенной форме (на Псевдокоде):
S3=S2 * U3 для i от 2 до n повторить
S4=S3 * U4 Si=Si-1 * Ui - рекуррентная формула (от слова рекурсия)
. . . . . .
Sn=Sn-1 * Un
В этой последовательности начиная со второй строки хорошо видна однотипность вычислений. Поэтому, заметив эту однотипность, попытаемся найти обобщенную запись. Обобщенная запись последовательности шагов, на каждом из которых последующее значение результата получается с использованием предыдущего, называется рекуррентной формулой (от слова рекурсия). Рекурсия в общем случае - это выражение (определение) какого-то понятия самого через себя. В данном случае осуществляется вычисление нового значения переменной S через ее старое значение (i-е промежуточное значение S вычисляется через (i-1)-ое). Если удалось получить такую обобщенную формулу, то это означает, что можно свернуть группу действий (для которой удалось найти обобщенную запись) в цикл (с заранее известным числом повторений). В общем случае цикл будет состоять из трех частей (порядок их важен):
Подготовка
Заголовок
Тело
В тело цикла включается то, что удалось записать в виде рекуррентной формулы, т.е. тело цикла - это те действия, которые надо многократно повторять. Заголовок цикла задает закон изменения т.н. параметра цикла, из которого определяется количество повторения цикла (из приведенного выше заголовка цикла видно, что цикл будет выполняться n-1 раз для i от 2 до n). В подготовку цикла включаются те действия, которые не удалось подвести под рекуррентную формулу. Подготовка цикла настраивает цикл на первое правильное выполнение. На Псевдокоде цикл для выполнения рассмотренной выше последовательности действий имеет вид:
подготовка S1=U1
заголовок Для i от 2 до n повторить
тело цикла Si=Si-1 * Ui
Согласно «Правил разработки циклов» (чуть позже рассмотрим) мы имеем дело с циклом с известным числом повторений, которые разрабатываются в данном случае методом «снизу вверх».
Согласно Правил после получения записи цикла необходимо попытаться выполнить упрощение подготовки цикла. Подготовка бывает простой, если в правой части оператора присваивания используется константа или переменная без индекса.
В данном случае подготовка простой не является, потому что в правой части используется переменная U1 - с индексом. Для упрощения подготовки составляется система уравнений:
- в 1-е уравнение переписывается сам оператор присваивания из подготовки цикла;
- 2-е уравнение получается из рекуррентной (обобщенной) формулы путем подстановки в нее (в левую и правую часть оператора присваивания) нужных значений (тех, которые используются в подготовке) индексов (в данном случае i=1):
| U1 = S0 * U1 |
S1=S0 * U1
Частные случаи:
- если обобщенная операция "+", то S0=0 ;
- если обобщенная операция "*", то S0=1.
В общем случае присваивание для простой подготовки цикла должно иметь вид: S0=const.
Если попытка упрощения подготовки цикла удалась, то необходимо скорректировать заголовок цикла таким образом, чтобы число повторения цикла увеличилось на единицу. Это нужно сделать потому что в результате упрощения подготовки цикла действия которые ранее выполнялись при подготовке (т.е. вне цикла), теперь включаются в тело цикла и нужно еще один проход тела цикла выполнить, что бы эти действия выполнялись.
В данном случае цикл примет следующий вид:
S0:=const;
Для i от 1 до n повторить
Si:=Si-1 * Ui
Далее согласно теории (См п. «Использование индексов в математике и программах») необходимо исключить лишние индексы. В результате получится следующий вид цикла.
S = const
Для i от 1 до n повторить
S=S * Ui
Часто бывают такие ситуации, когда компоненты многоместных операций представляют из себя не простые выражения (как в рассмотренном выше случае), а достаточно сложные.
Например:
n
S= 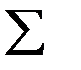 xi
xi
i=1
В данном случае нужно привести сложную запись каждого операнда многоместной операции к более простой форме , которая была до этого.
n n
S= 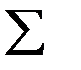 xi =
xi = 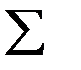 ui , где ui = xi
ui , где ui = xi
i=1 i=1
более простая запись
Далее в дополнение к поиску обобщенной формулы для самой многоместной операции необходимо попытаться найти обобщенную запись для вычисления каждой сложной компоненты многоместной операции вида: Ui = f(Ui-1) . При этом самый простой способ для нахождения нужной формулы – это деление типа
Z=Ui/Ui-1.
Тогда при известном Z можно вычислить Ui через Ui-1:
Ui=Z*Ui-1
Для данного примера такая формула имеет следующий вид: Ui=Ui-1∙x
Замечание: вместо деления аналогичным образом можно выполнить вычитание.
Если попытка нахождения обобщенной записи каждой сложной компоненты многоместной операции удалось, то дальше можно выполнять те же действия, что и для более простого предыдущего случая за одним только исключением: При записи линейного алгоритма (и при записи тела цикла) вместо одного действия у нас на каждом этапе (на каждой итерации) будет два:
вычислить U1=X для шагов, начиная со 2-го можно записать
| Составной оператор |
вычислить U2=U1*X нач
принять S2=S1+U2 Ui=Ui-1*X
вычислить U3=U2*X Si=Si-1+Ui
принять S3=S3+U2кон
............
В подготовке теперь тоже будет не одно действие, а два:
1) Вычислить U1=X
2) Принять S1 = U1
Упростим эту подготовку:
| S1=U1 S1=S0+U1 |
| U1= X U1=U0*X |
| После исключения лишних индексов получим: S=0; U=1 Для i от 1 до n повторить нач U=U*X S=S+U кон |
S0 = 0
упрощенная подготовка цикла
U0 = 1
В итоге получим следующий цикл.
S0=0; U0=1
Для i от 1 до n повторить
нач
Ui=Ui-1*X
Si=Si-1+Ui
кон
10.7 Подведение выражения под n-арную операцию (нахождение компактной записи).
Часто встречаются такие случаи, когда необходимо длинную последовательность действий подвести под цикл:
S=1+3/4+4/6+5/8+...= 1 + 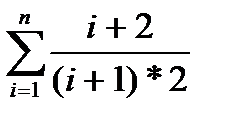
Подходов к решения этой задачи много. Самыми простейшими из них являются следующие:
а) поделить все следующие элементы последовательности на предыдущие и попробовать получить геометрическую прогрессию
Например:
S = 1 + ½ + ¼ + 1/8 ++ ...
Возможны два варианта нахождения решения: 1) решение вида ai = f(i), т.е. нахождение формулы для прямого вычисления элементов ряда 2) решение вида ai = f(ai-1), т.е. нахождение формулы для вычисления Текущего значения элемента ряда из предыдущего значения.
Для нахождения обоих видов решения надо составить таблицу:
| ai | ½ | 1/4 | 1/8 | 1/16 |
| i |
Из таблицы видно, что обобщенные формулы для двух видов решения имеют вид:
S = 1 + 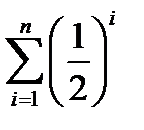 или S = 1 +
или S = 1 + 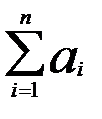 , где ai = ai-1 *(1/2)
, где ai = ai-1 *(1/2)
обобщенная запись вида ai = f(ai-1)
ai (здесь нужна подготовка цикла: S0 := 1;
a0 := 1)
обобщенная запись вида ai = f(i)
(здесь подготовка цикла не нужна)
б) вычесть из последующих значений ряда предыдущие и попробовать получить арифметическую прогрессию, т.е. представить все последующие элементы как предыдущий плюс некоторую разность
Например:
S = 1 + 3 + 5 + 7+ 9 + 11 = 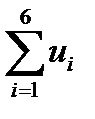
Для нахождения обобщенной формулы, как уже говорилось выше, есть 2 пути:
1 путь: угадать обобщенную формулу для прямого (без рекурсии) вычисления каждого элемента последовательности
| ui | ||||||
| i |
Из таблицы видно, что ui = 2*i – 1 (здесь подготовка цикла не нужна)
В итоге получим цикл:
S :=0;
For i:=1 to 6 do
S := S + 2*i – 1
2 путь: угадать рекуррентную формулу для вычисления ui вида: ui = f(ui-1)
| ui | ||||||
| i |
Из таблицы видно, что ui = ui-1 + 2 (для i от 2 до 6)
(здесь подготовка цикла нужна:
| u0 = 1-2 = -1 |
u1 = u0 +2;
В итоге получим цикл:
S :=0; u :=-1;
for i:=1 to 6 do
begin
u := u + 2;
S := S + u;
end;
в) попытаться подвести под цикл не всю последовательность, а ее часть, например, выкинув (исключив) из анализа первый элемент (мысленно)
Например:
s = 1+3+5+7+9+11= 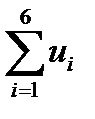 = 1+
= 1+ 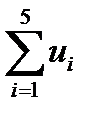
Выше (в пункте б) мы рассмотрели ситуацию, когда эта последовательность подводилась под цикл с первого элемента. Теперь рассмотрим ситуацию, когда ту же последовательность будем подводить под цикл, начиная со второго элемента (первый уйдет в подготовку цикла):
| ui | |||||
| i |
Из таблицы видно, что при прямом вычислении ui = 2i+1 (для i от 1 до 5)
Здесь подготовка цикла нужна только для S (s0 = 1):
В итоге получим цикл:
S :=1;
For i:=1 to 5 do
S := S + 2i+1;
Из той же таблицы видно, что при рекурсивном вычислении ui имеем:
ui = ui-1+2 (для i от 1 до 5)
Здесь подготовка цикла нужна и для S (s0 = 1) и для u:
| u0 = 3-2 = 1; |
u1 = u0 +2;
В итоге получим цикл:
S :=1; u:=1;
for i:=1 to 5 do
begin
u := u+2;
S := S + u;
end;
г) Если не удается найти обобщенную запись для дробного выражения в целом, надо представить дробь в виде следующей общей записи:
n
S= 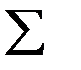 ai/bi
ai/bi
i=1
После этого отдельно для числителя и знаменателя расписывается последовательность значений. Так для случая
S=1+3/4+4/6+5/8+...
получим:
| ai = i +1 |
| bi = 2*i |
S = 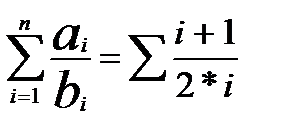
|
| ai | |||||
| i |
| bi | |||||
| i |
a1 /b1 = 1
Замечание:
Часто ряд значений бывает знакопеременным, например
S=1 - 3/4+4/6 - 5/8+6/10...= 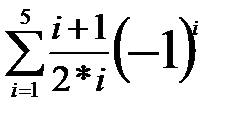
В этом случае в программе категорически не надо возводить (-1) в степень. Вместо этого надо завести дополнительную переменную a и делать так:
{Подготовка}
a:=1; {Знак a специально подбирается исходя из того, перед каким элементом ряда – четным
или нечетным стоит знак минус}
s:=0;
{Тело цикла}
.....
a := a * (-1); {инвертируем - переключаем знак a при каждом повторении тела}
S := S +((i+1)/(2*i))*a; { меняем знак у слагаемого путем умножения на a}
.....
11. Средства языка Паскаль для циклов с известным числом повторений.
| begin оператор1 оператор2 оператор3 ... end; |
| В том числе и оператор цикла (вложенные циклы) |
Такие циклы называются еще счетными циклами или циклами с параметром. Форма записи таких циклов имеет вид:
For <параметр> := <начальное значение> to <конечное значение> do оператор;
или
For <параметр> := <начальное значение> downto <конечное значение> do оператор;
1.один оператор
2.пустой оператор
3.составной оператор
...do ; ...
Параметр цикла это переменная, закон изменения которой задает количество повторений цикла. Значения параметра цикла будут изменяться от начального значения до конечного (или от конечного до начального). Шаг изменения параметра цикла фиксирован и равен единице (для верхнего примера +1, для нижнего (-1)). Параметр цикла по правилам Паскаля может быть любым порядковым типом (целым, булевским, символьным, перечисляемых, типом - диапазоном). Тело цикла будет повторяться для каждого значения параметра цикла.
Замечание: если нужно, чтобы вещественная переменная (а не порядковая) изменялась с некоторым (постоянным) шагом, то это можно сделать так:
Var
r:real;
i:integer;
begin
r:=0.0;
for i:=1 to 10 do
| Логическое выражение |
или r будет изменяться от 0 до 1.0 с шагом 0.1
r := (i-1) * 0.1;
Порядок выполненияоператора цикла следующий:
1). Проверяется значение следующего логического выражения:
для верхнего "начальное значение" <= " конечное значение"
для нижнего "начальное значение" >= " конечное значение"
Если это логическое выражение имеет значение "истина", то параметр цикла получает начальное значение и цикл выполняется дальше, т.е. переходим к п.2.
Если значение выражения "ложь", то параметр цикла не получает начального значения и цикл ни разу не выполняется, т.е. не переходим к п.2.
2). Дальнейшее выполнение цикла проходит следующие шаги:
2.1 Выполняются действия в теле цикла
2.2 Проверяется соотношение текущего значения параметра цикла с конечным значением, Вид соответствующего (проверяемого) логического выражения зависит от вида цикла:
| Логическое выражение |
для верхнего примера параметр цикла < " конечное значение"
для нижнего примера параметр цикла > " конечное значение"
Если это логическое выражение имеет значение "истина", то будет изменено на +1 (для верхнего случая) или -1 (для нижнего случая) значение параметра цикла и выполнен еще один повтор тела цикла, т.е. будет еще раз повторен пункт 2.
Если это логическое выражение имеет значение "ложь", то выполнение цикла завершится.
Рассмотрим два простых примера:
1) 2)
Var Var
| выводится оператором writeln после цикла |
begin begin
i:=-2; i:=-2
for i:=0 to 4 do for i:=0 to -1 do
writeln(i); writeln(i);
writeln(i); writeln(i);
end. End.
1)Цикл будет выполняться пять раз. 2)Цикл не будет выполняться не разу потому, что
Выведет значение i : 0, 1, 2, 3, 4, 4 начальные условия (см. п.1) не выполняются. В результате
По выходу из цикла параметр действия, включения в цикле будут пропущены
цикла равен последнему значению Writeln(i) выведет (-2). Начальное значение параметр цикла
при котором последний раз получает после того, как цикл начинает выполняться.
выполнялось тело цикла.
В Турбо Паскале, начиная с 7-й версии, появились 2 псевдооператора, которые позволяют менять ход выполнения цикла:
For i := 1 to 10 do
| если циклы вложенные (телом цикла является цикл) |
...
break;
continue;
...
end;
Break - позволяет выполнить внезапный (одноуровневый) выход из цикла.
Continue выполняет следующее:
- прерывается текущее выполнение тела цикла при текущем значении параметра цикла
- изменяется значение параметра цикла на следующее
- начинается следующая итерация цикла (со следующим значением параметра цикла).
Дата добавления: 2016-05-28; просмотров: 2365;











