Лекция 9-10 ИНДЕКСНЫЙ СТАТИСТИЧЕСКИЙ АНАЛИЗ
Понятие и классификация статистических индексов
Индексы являются одними из важнейших статистических показателей. В статистике под индексом понимается относительная величина, показывающая, во сколько раз уровень социально-экономического явления в данных условиях отличается от его же уровня в других условиях. При этом различие условий может проявляться во времени, в пространстве или в сравнении с эталоном.
С помощью индексов решаются следующие задачи статистического анализа:
· анализ динамики социально-экономического явления за два и более периодов времени;
· анализ динамики среднего статистического показателя;
· сравнительный анализ статистических показателей по разным территориям (регионам, странам);
· анализ влияния изменений значений одних статистических показателей на динамику других;
· пересчет значения макроэкономических показателей из фактических цен в сопоставимые.
Каждая из этих задач решается с помощью различных индексов.
В теории статистики принята следующая классификация индексов.
По степени охвата явления индексы бывают индивидуальные и сводные. Индивидуальные индексы характеризуют изменение отдельных элементов явления. Например, индивидуальным является индекс цен на молоко как элемент товаров молочной группы. Индивидуальные индексы принято обозначать символом 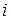 . Сводные индексы характеризуют изменение какого-либо показателя, рассчитанного для группы элементов явления или явления в целом (например, изменение цен на товары молочной группы). Сводные индексы принято обозначать символом
. Сводные индексы характеризуют изменение какого-либо показателя, рассчитанного для группы элементов явления или явления в целом (например, изменение цен на товары молочной группы). Сводные индексы принято обозначать символом 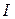 .
.
По базе сравнения вес индексы можно разделить на две группы: динамические и территориальные. Динамические индексы отражают изменение явления во времени. Например, индекс цен на продукцию в текущем году по сравнению с предыдущим годом или по сравнению с базисным годом (в качестве базисных цен могут быть использованы их плановые или прогнозные значения). В первом случае индексы называют цепными, во втором – базисными. Территориальные индексы позволяют сопоставлять уровень явления в пространстве. Например, индекс цен на продукцию одного региона по сравнению с другим.
В зависимости от формы построения различают агрегатные и средние сводные динамические индексы. Агрегатная форма является основной формой построения сводных индексов. Средняя форма является производной от агрегатной формы и заключается в усреднении значений индивидуальных индексов, рассчитанных для отдельных элементов исследуемого явления. При этом используется два способа усреднения – на основе формулы средней арифметической и формулы средней гармонической.
Сводное индексирование отдельных статистических показателей во временном аспекте требует использования в качестве весов значения других показателей. Например, индексируя цены на группу товаров, необходимо взвешивать ее значения по соответствующим значениям физического объема этих товаров. Если при этом индексы рассчитывают за ряд временных периодов, то в зависимости от вида весов возможны два варианта расчета – с постоянными и переменными весами. В первом случае значения весов берутся из одного и того же периода, во втором случае – из разных периодов. Это деление производится независимо от способа построения индекса – цепного или базисного.
По объекту исследования индексы бывают: трудовых затрат, себестоимости, физического объема продукции, цен, стоимости продукции и т. д.
По характеру объема исследования индексы подразделяются на индексы количественных (объемных) и качественных показателей. К первой группе индексов относятся, например, индексы физического объема производства продукции, а ко второй – индекс цен на эту продукцию, индекс ее себестоимости и т. д.
По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава. Деление индексов на эти две группы используется для факторного анализа динамики средних статистических показателей.
По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.
Индивидуальные и сводные индексы
Рассмотрим порядок расчета индивидуальных индексов на примере реализации конкретного товара.
Относительное изменение цены товара характеризуется индивидуальным индексом цен
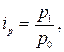
где р1, р0 – цена товара в текущем и предшествующем (базисном) периоде.
Для оценки относительного изменения объема реализации товара в натуральном выражении рассчитывают индивидуальный индекс физического объема
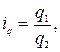
где q1, q2 – количество товара, проданного в отчётном и базисном периоде соответственно.
Произведение индивидуальных индексов цен и физического объема дает индивидуальный индекс стоимости:
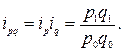
Этот индекс характеризует относительное изменение товарооборота, то есть стоимости всего реализованного товара.
В общем случае, индивидуальный индекс показывает, во сколько раз изменилось значение индексируемого показателя для отдельного элемента явления (в данном конкретном случае – для отдельного товара) при изменении условий его расчета (при смене предшествующего или базисного периода на текущий период).
Пример 11.1. В таблице 11.1 представлены данные о динамике выпуска продукции машиностроительным заводом.
Таблица 11.1
| Вид продукции | Выпуск | Цена, млн.руб. | ||
| базисный год | отчётный год | базисный год | отчетный год | |
| Оборудование, шт. | 75,00 | 82,50 | ||
| Литье, т | 8,75 | 10,10 |
Оценим относительную (в %) динамику цен, физического объема и товарооборота по каждому виду продукции.
Решение.
Рассчитаем индивидуальные индексы цен и физического объема для каждого товара:
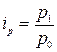 ;
;
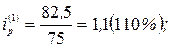
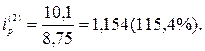
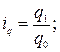
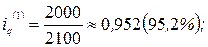
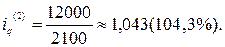
На основе индивидуальных индексов цен и физического объема рассчитаем индивидуальный индекс стоимости (товарооборота) для каждого товара:
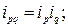
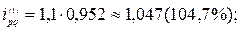
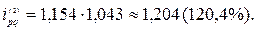
Таким образом, в отчетном году по сравнению с базисным годом цена на оборудование выросла на 10%, его физический объем снизился на 4,8%, что в итоге привело к увеличению товарооборота на 4,7%. Цена, физический объем и товарооборот литья увеличились соответственно на 15,4%, 4,3% и 20,4%.
Сводный индекс, в отличие от индивидуального, является более сложным относительным показателем, поскольку характеризует среднее изменение социально-экономического явления, структурно состоящего из отдельных элементов.
Самый простой вариант расчета сводного индекса – расчет в агрегатной форме (agregatus означает суммарный). Например, сводный индекс стоимости товаров определяют следующим образом:
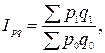
где:
p – цена на отдельные товары;
q – количество товара в натуральном выражении.
Этот индекс показывает, во сколько раз изменилась общая стоимость проданных товаров в текущем периоде относительно базисного. Ему соответствует абсолютное изменение стоимости товаров
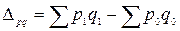 .
.
При расчете сводного индекса цен учитывают вес каждого товара в общем физическом объеме реализации. Если веса берут из предшествующего (базисного) периода, то имеет место сводный индекс цен Ласпейреса
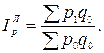
Если веса берут из текущего периода, то говорят о сводном индексе цен Пааше
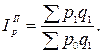
Оба индекса показывают, во сколько раз изменилась общая стоимость проданных товаров из-за изменения цен на них или во сколько раз в среднем изменились цены на товары. Индексам соответствуют абсолютные изменения стоимости под влиянием изменения цен:
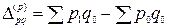 ;
;
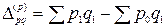 .
.
При расчете сводного индекса физического объема в качестве весового показателя используют цену товара:
· по методу Ласпейреса
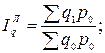
· по методу Пааше
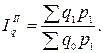
При этом существует два равнозначных варианта интерпретации значений этих индексов:
1) индекс показывает, во сколько раз в среднем (в целом) изменился физический объем реализации;
2) индекс показывает, во сколько раз изменилась общая стоимость реализованных товаров из-за изменения количества каждого из них.
Индексам физического объема Ласпейреса и Пааше соответствуют абсолютные изменения стоимости реализованных товаров, обусловленные изменение их физического объема:
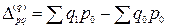 ;
;
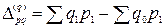 .
.
Сводные индексы цен, физического объема, стоимости и соответствующие им абсолютные изменения стоимости связаны между собой:
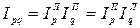 ;
;
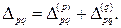
Обычно до окончания текущего периода отсутствуют точные сведения о физическом объеме реализации товаров. В этом случае сводный индекс цен рассчитывают по методу Ласпейреса, а сводный индекс физического объема – по методу Пааше. По окончании текущего периода делают ретроспективный расчет индексов, меняя методы расчета на альтернативные.
Аналогичные формулы индивидуальных и сводных индексов используют при индексном анализе динамики других экономических показателей.
Пример 11.2. В таблице 11.2 представлены данные о динамике себестоимости и физического объема продукции завода почвообрабатывающих машин в первом полугодии отчетного года.
Таблица 11.2
| Вид продукции | Физический объем, шт. | Себестоимость, тыс. руб. | ||
| I квартал | II квартал | I квартал | II квартал | |
| Плуги навесные | 4,8 | 5,4 | ||
| Плуги прицепные | 7,1 | 7,6 | ||
| Культиваторы | 5,0 | 5,7 |
Оценим относительную динамику физического объема, себестоимости и издержек, связанных с производством продукции в целом.
Решение.
Обозначим:
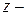 себестоимость отдельного вида продукции;
себестоимость отдельного вида продукции;
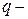 ее физический объем;
ее физический объем;
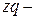 издержки, связанные с ее производством в заданном объеме.
издержки, связанные с ее производством в заданном объеме.
Выберем для расчета сводного индекса физического объема метод Ласпейреса, а для сводного индекса себестоимости – метод Пааше.
В результате:
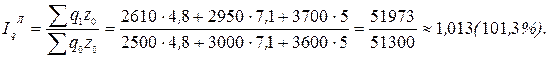
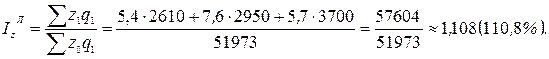
На основе полученных индексов рассчитаем сводный индекс издержек
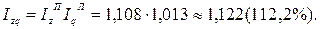
Таким образом, в целом физический объем производимой заводом продукции увеличилась на 1,3%, ее себестоимость выросла на 10,8%, что в итоге привело к увеличению издержек на 12,2%.
Пример 11.3. В таблице 11.3 представлены данные о динамике затрат рабочего времени на единицу продукции и ее физического объема по машиностроительному заводу.
Таблица 11.3
| Вид продукции | Затраты рабочего времени на единицу продукции, чел∙час. | Физический объем, шт. | ||
| базисный год | отчетный год | базисный год | отчетный год | |
| Станки-автоматы | ||||
| Станки-полуавтоматы |
Рассчитаем:
1) сводные индексы затрат рабочего времени на единицу продукции Ласпейреса, физического объема Пааше и общих затрат рабочего времени;
2) абсолютное изменение общих затрат рабочего времени в целом, а также отдельно под влиянием изменения затрат на единицу продукции и ее физического объема.
Решение.
Обозначим:
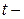 затраты рабочего времени на единицу продукции отдельного вида;
затраты рабочего времени на единицу продукции отдельного вида;
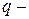 ее физический объем;
ее физический объем;
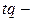 общие затраты рабочего времени на производство продукции отдельного вида.
общие затраты рабочего времени на производство продукции отдельного вида.
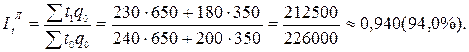
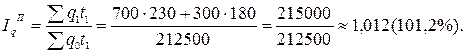
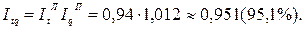
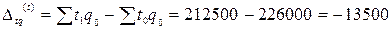 чел∙час.
чел∙час.
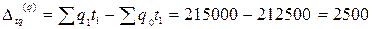 чел∙час.
чел∙час.
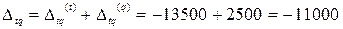 чел∙час.
чел∙час.
Таким образом, по методу Ласпейреса затраты рабочего времени на единицу продукции снизились на 6%, что привело к снижению общих затрат на 13500 чел∙час. Физический объем продукции вырос по методу Пааше на 1,2%, что привело к увеличению общих затрат на 2500 чел∙час. В результате совместного действия обоих факторов общие затраты рабочего времени снизились на 11000 чел∙час. или на 4,9%.
Индексы, рассчитанные по методу Ласпейреса и Пааше, как правило, не совпадают. Например, при наличии инфляции всегда выполняется неравенство
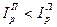 .
.
Это происходит из-за того, что при росте цен потребители заменяют дорогие товары на более дешевые. В таких случаях в качестве единого сводного индекса используют индекс цен Фишера
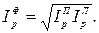
Особенностью индекса Фишера является его обратимость во времени. Если сравниваемые периоды поменять местами, то новый индекс Фишера будет обратной величиной по отношению к старому, то есть
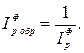
Следовательно, этот индекс можно использовать в обоих направлениях. Индексы Ласпейреса и Пааше такой возможности лишены. Зато, в отличие от индекса Фишера, эти индексы имеют четкий экономический смысл. Разница между числителем и знаменателем в их формулах показывает экономию (ущерб) потребителей из-за изменения цен на товары или из-за изменения их количества.
Для вычисления сводных индексов в агрегатной форме необходимы данные за оба сравниваемых периода. Если данные имеются только за один из периодов, но при этом известны индивидуальные индексы, то для расчета сводных индексов используют формулы средней – арифметической или гармонической.
Если, например, известны данные о стоимости товаров в базисном периоде и значения индивидуальных индексов стоимости, то сводный индекс стоимости рассчитывают по формуле средней арифметической:
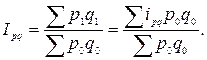
В этой формуле усредняют индивидуальные индексы стоимости, взвешивая их по стоимости товара в базисном периоде.
При наличии данных за текущий период используют формулу среднюю гармоническую:
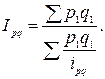
На выбор формулы средней также влияет метод расчета сводного индекса – Ласпейреса или Пааше, например:
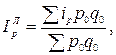
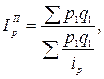
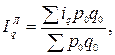
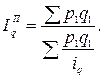
Аналогичные формулы применяют при усреднении индивидуальных индексов других экономических показателей.
Пример 11.4. В таблице 11.4 представлены данные о динамике производства продукции металлургическим заводом. Оценим относительную динамику физического объема продукции по заводу в целом, используя метод индексирования Ласпейреса.
Таблица 11.4
| Вид продукции | Стоимость в I квартале, тыс. руб. | Изменение физического объема во II квартале по сравнению с I кварталом, % |
| Рельсы трамвайные | +3,1 | |
| Чугун литейный | - 2,5 | |
| Железо листовое | +1,6 |
Решение.
Представленные в третьей графе таблицы 11.4 задают значения индивидуальных индексов физического объема:
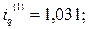
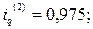
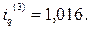
Учитывая характер исходных данных и метод индексирования, рассчитаем сводный индекс физического объема по формуле средней арифметической:
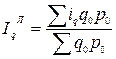
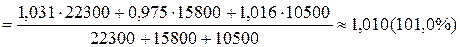 .
.
Полученное значение индекса свидетельствует об увеличении физического объема продукции в целом на 1 %.
Пример 11.5. В таблице 11.5 представлены данные о динамике себестоимости и издержках производства продукции деревообрабатывающим заводом. Оценим относительную динамику себестоимости продукции завода в целом, используя метод индексирования Пааше.
Таблица 11.4
| Вид продукции | Индивидуальный индекс себестоимости | Издержки в отчетном году, млн. руб. |
| Доска обрезная | 1,08 | |
| Доска-вагонка | 1,09 |
Решение.
Учитывая характер исходных данных и метод индексирования, рассчитаем сводный индекс себестоимости продукции по формуле средней гармонической:
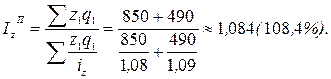
Таким образом, себестоимость продукции в целом выросла на 8,4%.
Системы индексов
При изучении динамики уровней социально-экономического явления за три и более периодов времени формируют систему индексов. Если при этом явление имеет однотоварный характер, то строят систему индивидуальных индексов – базисных или цепных.
Например, при изучении динамики цен конкретного товара относительно базисного периода формируют систему индивидуальных базисных индексов цен
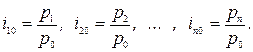
Если вместо постоянной базы сравнения используют предшествующие периоды времени, то имеет место система цепных индексов:
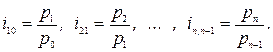
При изучении динамики многотоварных явлений используют системы сводных индексов. Если при этом индексируемые показатели не требуют применения весов, то соответствующие им системы сводных индексов строятся аналогично системам индивидуальных индексов.
Например, системы сводных индексов стоимости имеют вид:
· базисная
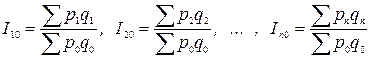 ;
;
· цепная
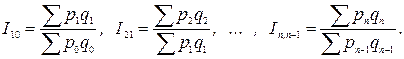
При взвешивании индексируемого показателя используют постоянные или переменные веса. Например, система сводных индексов физического объема с постоянными весами строится следующим образом:
· базисная
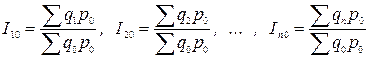 ;
;
· цепная
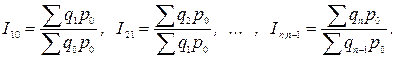
Если веса при переходе от одного индекса к другому меняются, то имеет место система сводных индексов с переменными весами. Например, система сводных индексов цен:
· базисная
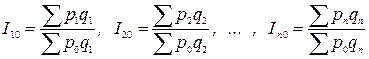 ;
;
· цепная
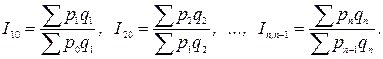
Базисные сводные индексы цен с переменными весами называют индексами-дефляторами. Их используют для пересчета стоимостных показателей в сопоставимые цены. Например, для пересчета ВВП страны за k-ый год в цены базисного года используют формулу
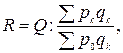
где:
R – реальное значение ВВП (в ценах базисного года);
Q – номинальное значение ВВП (в ценах k-го года);
pk, qk – цены и физический объём товаров, работ и услуг в структуре ВВП за k-ый год;
p0 – цены этих товаров, работ и услуг в базисном году.
Индивидуальные базисные и цепные индексы вязаны между собой. Например, базисный и цепной индивидуальные индексы цен для k-го периода времени могут быть определены соответственно по формулам:
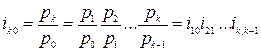 ;
;
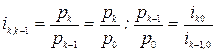 .
.
Аналогично связаны между собой базисные и цепные сводные индексы, рассчитываемые без весов или с постоянными весами:
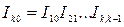 ;
;
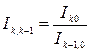 .
.
Для сводных индексов с переменными весами эти равенства не выполняются.
Пример 11.6. В таблице 11.6 представлены данные о динамике цен и физического объема продукции металлургического комбината.
Таблица 11.6
| Вид продукции | Отпускная цена за тонну, руб. | Выпуск, т | ||||
| I квартал | II квартал | III квартал | I квартал | II квартал | III квартал | |
| Прокат листовой | ||||||
| Сталь арматурная |
Сформируем системы сводных индексов для оценки цепной ежеквартальной динамики цен, физического объема и стоимости продукции комбината. При индексировании цен используем метод Пааше, при индексировании физического объема – метод Ласпейреса. В обоих случаях применим переменные веса.
Решение.
Цепные сводные индексы физического объема с переменными весами:
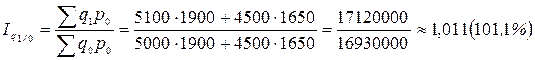 ;
;
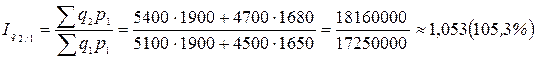 .
.
Таким образом, физический объем продукции во II квартале вырос на 1,1%, в III квартале – на 5,3%.
Цепные сводные индексы цен с переменными весами:
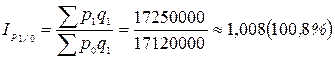 ;
;
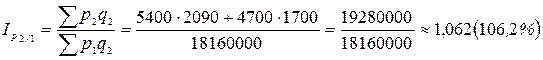 .
.
Таким образом, цены на продукцию во II квартале выросли на 0,8%, в III квартале – на 6,2%.
Цепные сводные индексы стоимости:
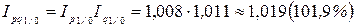 ;
;
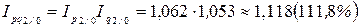 .
.
Таким образом, стоимость выпускаемой металлургическим комбинатом продукции во II квартале выросла на 1,9%, в III квартале – на 11,8%.
Дата добавления: 2022-07-20; просмотров: 258;











