Корреляционный анализ рядов динамики
В главе 9 были рассмотрены методы статистического изучения взаимосвязи между социально-экономическими явлениями и процессами в пространственном аспекте на основе корреляционного анализа значений статистических признаков. Например, таким образом можно оценить зависимость урожайности зерновых культур от количества внесенных в землю удобрений, используя в качестве исходных данных значения этих признаков для различных земельных участков. Вместе с тем, аналогичное исследование может быть проведено во временном аспекте посредством анализа взаимосвязи между рядом динамики урожайности и рядом динамики внесенных удобрений, сформированных для одного и того же земельного участка за ряд лет временных периодов.
Однако методы корреляционного анализа статистических признаков могут быть применены в отношении рядов динамики с учетом определенных ограничений. Дело в том, что если ряд динамики содержит только случайную компоненту (уровни колеблются относительно среднего значения случайным образом), то значения уровней являются такими же независимыми, как и значения статистического признака. В этом случае методы корреляционного анализа, рассмотренные в главе 9, могут быть применены в отношении временных уровней статистических показателей без дополнительных ограничений. Однако, если в ряду присутствует основная тенденция и (или) циклические (сезонные) колебания, то значения уровней будут зависеть от фактора времени. Следовательно, последующие значения уровней будут зависеть от их предшествующих значений. В этом случае использование традиционных показателей для оценки корреляции между рядами динамики приведет к завышению или занижению этой оценки. Например, если оба ряда содержат основную тенденцию или колебания с одинаковой периодичностью, то это завышает оценку тесноты взаимосвязи между ними. Если основная тенденция или колебания присутствуют только в одном из рядов, а также если в обоих рядах наблюдаются циклические (сезонные) колебания, имеющие разную периодичность, то это занижает оценку взаимосвязи.
Таким образом, прежде чем оценивать взаимосвязь между рядами динамки, необходимо выяснить, имеется ли в каждом из них автокорреляция уровней, то есть зависимость последующих значений уровней от предыдущих значений. Для этого уровни исходного ряда последовательно сдвигают на одну, две, три и т. д. позиций в будущее (количество позиций этого сдвига называют лагом) и для полученных двух рядов динамики – исходного и сдвинутого, рассчитывают коэффициент автокорреляции
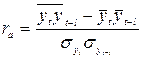 ,
,
где:
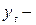 уровни исходного ряда динамики;
уровни исходного ряда динамики;
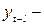 уровни сдвинутого ряда динамики;
уровни сдвинутого ряда динамики;
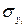 ,
, 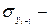 среднеквадратичные отклонения значений этих уровней;
среднеквадратичные отклонения значений этих уровней;
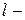 лаг (порядок коэффициента автокорреляции).
лаг (порядок коэффициента автокорреляции).
Как видно из формулы, коэффициент автокорреляции – это парный коэффициент корреляции, применяемый не в пространственном, а во временном аспекте, но имеющий при этом такой же диапазон и интерпретацию абсолютных значений. Вместе с тем, по знаку коэффициента автокорреляции нельзя судить о направлении основной тенденции – прямом или обратном. Как правило, ряды динамики, имеющие убывающую тенденцию, тем не менее, характеризуются положительной автокорреляцией.
Недостатком использования коэффициента автокорреляции является низкая объективность результатов оценки зависимости последующих уровней от предыдущих, вызванной нелинейной тенденцией. В этом случае значение коэффициента может приближаться к нулю, что формально свидетельствует об отсутствии автокорреляции.
Кроме того, предварительный сдвиг уровней приводит к тому, что коэффициент автокорреляции рассчитывается на меньшем множестве наблюдений (число пар коррелируемых уровней уменьшается на величину лага). Это, в свою очередь, уменьшает значимость его высокого абсолютного значения.
Для оценки значимости расчетного значения коэффициента автокорреляции используют критерий
 .
.
В таблице 10.20 представлен ряд табличных значений коэффициента автокорреляции при уровне значимости 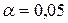 .
.
Таблица 10.20
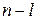
| 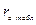
| |
при 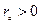
| при 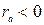
| |
| 0,253 | -0,753 | |
| 0,354 | -0,708 | |
| 0,370 | -0,674 | |
| 0,371 | -0,625 | |
| 0,366 | -0,593 | |
| 0,360 | -0,564 | |
| 0,353 | -0,539 | |
| 0,348 | -0,516 | |
| 0,341 | -0,497 | |
| 0,335 | -0,479 | |
| 0,328 | -0,462 | |
| 0,299 | -0,399 | |
| 0,276 | -0,356 | |
| 0,257 | -0,324 |
Последовательность коэффициентов автокорреляции первого, второго и т. д. порядков называют автокорреляционной функцией ряда динамики. График ее зависимости от величины лага (порядка коэффициента автокорреляции) называется коррелограммой.
Анализ значимости коэффициентов автокорреляции и зависимости их значений от величины лага позволяет определить фактические составляющие ряда динамики, помимо случайных колебаний уровней. Если наиболее высоким из значимых коэффициентов автокорреляции является коэффициент первого порядка, то исследуемый ряд содержит только основную тенденцию. Если наиболее высоким является значение коэффициента автокорреляции 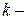 го порядка, то имеет место колебания уровней с циклом в
го порядка, то имеет место колебания уровней с циклом в 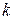 периодов времени. Если ни один из коэффициентов автокорреляции не является значимым, то это позволяет сделать два предположения:
периодов времени. Если ни один из коэффициентов автокорреляции не является значимым, то это позволяет сделать два предположения:
1) исследуемый ряд динамики не содержит ни основной тенденции, ни циклических (сезонных) колебаний и представляет собой случайные колебания уровней относительно их среднего значения;
2) имеет место нелинейная основная тенденция изменения уровней, для выявления и оценки которой необходимо провести дополнительный анализ.
Пример 10.12. В таблице 10.21 представлены данные динамики объема потребления электроэнергии ( 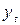 ) жителями региона за шестнадцать кварталов (
) жителями региона за шестнадцать кварталов ( 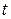 ). Определим структуру этого ряда, используя коэффициент автокорреляции.
). Определим структуру этого ряда, используя коэффициент автокорреляции.
Таблица 10.21
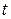
| ||||||||||||||||
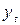
| 6,0 | 4,4 | 5,0 | 9,0 | 7,2 | 4,8 | 6,0 | 10,0 | 8,0 | 5,6 | 6,4 | 11,0 | 9,0 | 6,6 | 7,0 | 10,8 |
Решение.
Изобразим исходные данные графически (рис. 10.2).

Рис. 10.2
Полученная диаграмма позволяет предположить наличие в структуре ряда динамики линейной возрастающей основной тенденции и сезонных колебаний уровней с периодичностью в четыре квартала. Проверим это предположение, рассчитав коэффициенты автокорреляции различных порядков и построив соответствующую им коррелограмму.
Вначале рассчитаем коэффициент автокорреляции первого порядка, представив итерационную часть этого расчета в таблице 10.22.
Таблица 10.22
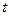
| 
| 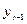
| 
| 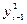
|  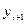
|
| 4,4 | 6,0 | 19,36 | 36,00 | 26,40 | |
| 5,0 | 4,4 | 25,00 | 19,36 | 22,00 | |
| 9,0 | 5,0 | 81,00 | 25,00 | 45,00 | |
| 7,2 | 9,0 | 51,84 | 81,00 | 64,80 | |
| 4,8 | 7,2 | 23,04 | 51,84 | 34,56 | |
| 6,0 | 4,8 | 36,00 | 23,04 | 28,80 | |
| 10,0 | 6,0 | 100,00 | 36,00 | 60,00 | |
| 8,0 | 10,0 | 64,00 | 100,00 | 80,00 | |
| 5,6 | 8,0 | 31,36 | 64,00 | 44,80 | |
| 6,4 | 5,6 | 40,96 | 31,36 | 35,84 | |
| 11,0 | 6,4 | 121,00 | 40,96 | 70,40 | |
| 9,0 | 11,0 | 81,00 | 121,00 | 99,00 | |
| 6,6 | 9,0 | 43,56 | 81,00 | 59,40 | |
| 7,0 | 6,6 | 49,00 | 43,56 | 46,20 | |
| 10,8 | 7,0 | 116,64 | 49,00 | 75,60 | |
| Итого | 110,8 | 106,0 | 883,76 | 803,12 | 792,80 |
В результате:
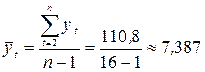 ;
; 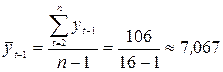 ;
;
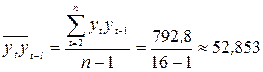 ;
;
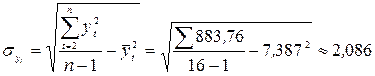 ;
; 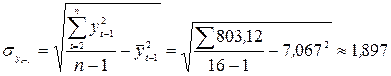 ;
;
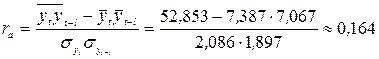 .
.
Аналогично рассчитываются значения коэффициентов автокорреляции последующих порядков (таблица 10.23).
Таблица 10.23
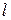
| ||||||||
| 0,164 | 0,567 | 0,114 | 0,983 | 0,119 | 0,722 | 0,003 | 0,974 |
 Тогда коррелограмма исследуемого ряда динамики имеет следующий вид (рис. 10.3).
Тогда коррелограмма исследуемого ряда динамики имеет следующий вид (рис. 10.3).
Рис. 10.3
Полученные результаты позволяют сделать следующие выводы:
1) в исследуемом ряду динамики присутствует возрастающая линейная основная тенденция. Об этом говорит наличие очень близких к единице значений коэффициентов автокорреляции;
2) в ряду также присутствуют сезонные колебания. Об этом свидетельствует низкое значение коэффициента автокорреляции первого порядка, сопровождающееся высокими значениями коэффициентов других порядков;
3) сезонные колебания уровней имеют периодичность в четыре квартала, поскольку максимум автокорреляционной функции соответствует временному лагу в четыре квартала. Кроме того, коэффициент автокорреляции восьмого порядка (кратного четырем) также имеет очень высокое значение.
Для оценки тесноты корреляционной связи между двумя рядами динамики при условии, что каждый из них лишен автокорреляции (в том числе обусловленной наличием нелинейной основной тенденцией), можно использовать те же показатели, что и для оценки тесноты связи между статистическими показателями – парный коэффициент корреляции и эмпирическое корреляционное отношение. При этом для проверки линейности корреляции можно использовать критерий, основанный на близости значений эмпирического и парного коэффициентов детерминации (см. параграф 9.2).
В случае выявления хотя бы в одном из рядов автокорреляции уровней для оценки взаимосвязи между рядами используют метод коррелирования отклонений. При этом вместо фактических уровней коррелируют их случайные компоненты, рассчитываемые по формулам:
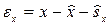 или
или 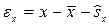 ;
;
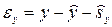 или
или 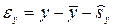 ,
,
где:
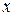 ,
, 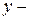 фактические значения уровней исследуемых рядов динамики;
фактические значения уровней исследуемых рядов динамики;
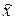 ,
, 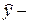 теоретические значения уровней, рассчитываемые при наличии основной тенденции по уравнению тренда;
теоретические значения уровней, рассчитываемые при наличии основной тенденции по уравнению тренда;
 ,
, 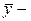 средние значения уровней, используемые при отсутствии основной тенденции;
средние значения уровней, используемые при отсутствии основной тенденции;
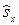 ,
, 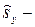 циклические (сезонные) отклонения уровней (при отсутствии соответствующих колебаний полагаются равными нулю);
циклические (сезонные) отклонения уровней (при отсутствии соответствующих колебаний полагаются равными нулю);
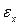 ,
, 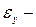 случайные колебания уровней.
случайные колебания уровней.
Направление и тесноту связи между случайными компонентами рядов динамики оценивают на основе коэффициента корреляции отклонений
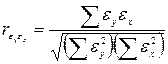 .
.
Его возможные значения укладываются в интервал от -1 до 1. Знак коэффициента указывает на направление связи: отрицательный – обратная, положительный – прямая. Чем ближе абсолютное значение этого показателя к единице, тем сильнее связь.
Пример 10.13. В таблице 10.24 представлены данные о динамике расходов на конечное потребление ( 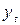 , усл. ед.) и совокупного дохода (
, усл. ед.) и совокупного дохода ( 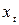 ) за ряд лет (
) за ряд лет ( 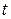 ).
).
Таблица 10.24
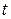
| ||||||||
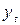
| ||||||||
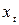
|
Оценим связь между представленными рядами динамики, исключив влияние фактора времени.
Решение.
Построим диаграмму динамики расходов на конечное потребление и совокупного дохода (рис. 10.4).

yt
хt
Согласно построенной диаграмме оба ряда динамики содержат линейную или близкую к линейной возрастающую основную тенденцию и не содержат каких-либо существенных циклических колебаний.
Рассчитаем значения коэффициента автокорреляции первого порядка отдельно для ряда динамики расходов на конечное потребление и ряда динамики совокупного дохода, представив итерационную часть этих расчетов в таблицах 10.25 и 10.26 соответственно.
Таблица 10.25
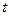
| 
| 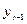
| 
| 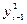
|  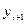
|
| Итого |
Таблица 10.26
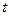
| 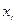
| 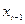
| 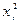
| 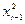
| 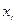 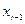
|
| Итого |
В результате:
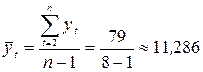 ;
;  ;
;
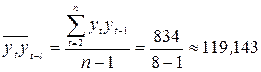 ;
; 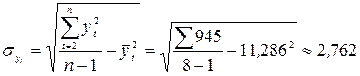 ;
;
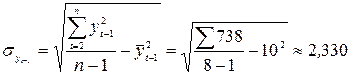 ;
;
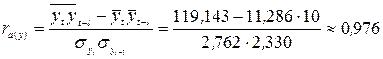 ;
;
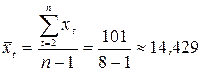 ;
; 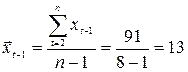 ;
;
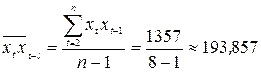 ;
;
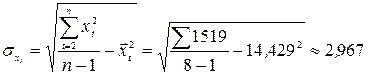 ;
;
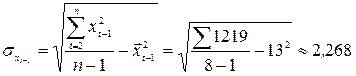 ;
;
 ;
;
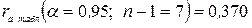 ;
;
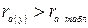 ;
; 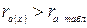 .
.
Полученные очень близкие к единице значимые коэффициенты автокорреляции первого порядка свидетельствуют о наличии сильной автокорреляции уровней в каждом ряду динамики и, соответственно линейной тенденции в их структуре.
Устраним выявленную тенденцию и оценим связь между исследуемыми рядами, рассчитав коэффициент корреляции отклонений. Итерационную часть этого расчета представим в таблице 10.27.
Вначале определим параметры соответствующих линейных уравнений тренда:
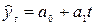 ;
; 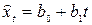 .
.
Вернемся к исходным данным и присвоим параметру 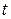 такие условные целые значения, при которых
такие условные целые значения, при которых 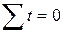 :
:
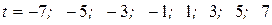 .
.
Тогда:
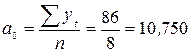 ;
; 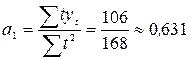 ;
;
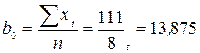 ;
; 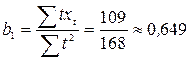 ;
;
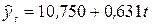 ;
; 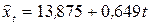 .
.
Таблица 10.27
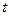
| 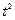
| 
| 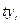
| 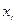
| 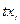
| 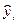
| 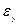
| 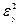
| 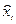
| 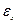
| 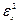
| 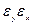
|
| -7 | -49 | -70 | 6,333 | 0,667 | 0,444889 | 9,332 | 0,668 | 0,446224 | 0,445556 | |||
| -5 | -40 | -60 | 7,595 | 0,405 | 0,164025 | 10,630 | 1,370 | 1,876900 | 0,554850 | |||
| -3 | -24 | -33 | 8,857 | -0,857 | 0,734449 | 11,928 | -0,928 | 0,861184 | 0,795296 | |||
| -1 | -10 | -12 | 10,119 | -0,119 | 0,014161 | 13,226 | -1,226 | 1,503076 | 0,145894 | |||
| 11,381 | -0,381 | 0,145161 | 14,524 | -0,524 | 0,274576 | 0,199644 | ||||||
| 12,643 | -0,643 | 0,413449 | 15,822 | -0,822 | 0,675684 | 0,528546 | ||||||
| 13,905 | 0,095 | 0,009025 | 17,120 | -0,120 | 0,014400 | -0,011400 | ||||||
| 15,167 | 0,833 | 0,693889 | 18,418 | 1,582 | 2,502724 | 1,317806 | ||||||
| Итого | 86,000 | 0,000 | 2,619048 | 111,000 | 0,000 | 8,154768 | 3,976192 |
Используя уравнения тренда, перейдем от фактических значений уровней к их случайным отклонениям от основной тенденции:
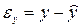 ;
; 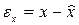 .
.
Затем рассчитаем коэффициент корреляции отклонений
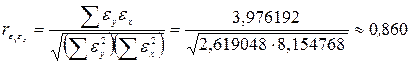 .
.
Таким образом, между уровнем совокупного дохода и уровнем расходов на конечное потребление существует сильная прямая связь.
Если ряд динамики содержит ярко выраженную линейную тенденцию (без существенных циклических или сезонный колебаний), то вместо метода коррелирования отклонений можно использовать более простой метод коррелирования разностей. При этом фактические значения уровней заменяют на цепные абсолютные приросты (разности первого порядка):
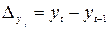 ;
; 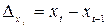 .
.
Затем рассчитывают коэффициент корреляции разностей
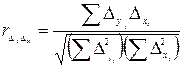 .
.
Интервал его значений и их интерпретация такие же, как и у коэффициента корреляции отклонений.
Пример 10.14. На основе исходных данных примера 10.13 оценим связь между уровнем конечных расходов на потребление и уровнем совокупного дохода, используя метод корреляции разностей.
Решение.
При рассмотрении примера 10.13 был обоснован ярко выраженный линейный характер основной тенденции в каждом из исследуемых рядов динамики. Это позволяет оценить тесноту связи между их уровнями на основе расчета коэффициента корреляции разностей первого порядка. Итерационную часть этого расчета представим в таблице 10.28.
Таблица 10.27
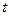
| 
| 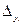
| 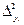
| 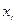
| 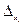
| 
| 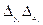
|
| - | - | - | - | - | |||
| -1 | |||||||
| Итого | - | - | - | - |
В результате:
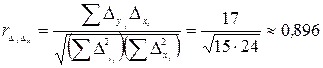 .
.
Таким образом, полученное значение коэффициента корреляции разностей первого порядка подтверждает сделанный в примере 10.13 вывод о сильной прямой связи между уровнем совокупного дохода и уровнем расходов на конечное потребление.
При наличии параболической тенденции вместо разностей первого порядка коррелируют разности второго порядка (разности между цепными абсолютными приростами), используя аналогичную формулу.
Прежде чем применять метод коррелирования разностей, целесообразно убедиться в отсутствии у них автокорреляции также, как это делается в отношении самих уровней. Это будет подтверждением предположения о характере основной тенденции (для разностей первого порядка – линейной, для второго порядка – параболической).
При всей своей простоте метод коррелирования разностей имеет существенный недостаток. Его применение связано с сокращением числа пар наблюдений, по которым оценивается взаимосвязь между рядами, что приводит к снижению достоверности результатов ее оценки.
Дата добавления: 2022-07-20; просмотров: 243;











