Лекция 8 Анализ сезонных колебаний уровней ряда динамики
Если уровни ряда динамики регулярно с интервалом в один год отклоняются от его основной тенденции, а при отсутствии этой тенденции – от среднего уровня, то это говорит о наличии в ряду сезонных колебаний. Так, например, сезонно колеблются уровни цен на овощи и фрукты: при наличии инфляции – относительно основной тенденции, при ее отсутствии – относительно среднегодовой цены.
Изучение сезонных колебаний осуществляют двумя методами – на основе расчета индексов сезонности и на основе гармонического анализа.
· Индексный метод анализа сезонных колебаний уровней ряда динамики.
В основе метода лежит расчет для каждого сезонного периода времени (месяца или квартала) соответствующего значения индекса сезонности.
Индекс сезонности – это относительный показатель динамики, определяющий, во сколько раз фактическое значение уровня за отдельный сезонный период времени отличается от значения уровня, соответствующего основной тенденции, а при ее отсутствии – от среднего значения уровня, рассчитанного на всем множестве сезонных периодов.
Порядок расчета индексов сезонности определяется наличием или отсутствием в ряду динамики основной тенденции и временными рамками ряда.
При отсутствии основной тенденции индекс сезонности для каждого месяца (квартала) рассчитывают по одной из формул:
· по данным за один год
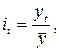
где
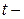 номер сезонного периода времени;
номер сезонного периода времени;
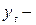 соответствующий ему уровень;
соответствующий ему уровень;
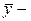 средний уровень за год;
средний уровень за год;
· по данным за ряд лет
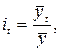
где:
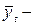 средний уровень за одноимённые сезонные периоды времени;
средний уровень за одноимённые сезонные периоды времени;
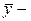 средний уровень за все годы.
средний уровень за все годы.
При наличии основной тенденции используют следующие формулы:
· по данным за один год
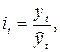
где 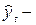 теоретический уровень (уровень основной тенденции), соответствующий сезонному периоду с номером
теоретический уровень (уровень основной тенденции), соответствующий сезонному периоду с номером 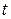 и рассчитанный по уравнению тренда или на основе метода скользящей средней (второй вариант – менее точный);
и рассчитанный по уравнению тренда или на основе метода скользящей средней (второй вариант – менее точный);
· по данным за ряд лет
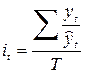 ,
,
где Т – число лет.
Обычно индексы сезонности выражают в процентах и используют в дальнейшем при построении сезонной волны. Сезонная волна – это график в виде ломаной кривой, описывающей зависимость величины индекса сезонности от сезонного периода времени. Она наглядно отображает характер сезонных колебаний уровней.
Пример 10.11. В таблице 10.17 представлены данные о динамике среднесуточного объема грузоперевозок (тыс. т) автотранспортного предприятия в период 2004 – 2006 гг. Рассчитаем ежемесячные индексы сезонности среднесуточного объема грузоперевозок, построим на их основе график сезонной волны и сделаем вывод о характере сезонных колебаний грузоперевозок.
Таблица 10.17
| Номер месяца | Год | ||
| 10,2 | 10,7 | 10,3 | |
| 10,4 | 10,3 | 10,5 | |
| 10,6 | 10,8 | 10,7 | |
| 11,0 | 10,9 | 11,3 | |
| 11,3 | 11,2 | 11,3 | |
| 11,5 | 11,0 | 11,7 | |
| 11,6 | 11,3 | 11,8 | |
| 12,0 | 11,7 | 12,4 | |
| 11,2 | 11,7 | 11,5 | |
| 10,9 | 10,7 | 10,8 | |
| 10,2 | 10,4 | 10,3 | |
| 10,0 | 9,9 | 10,1 |
Решение.
Вначале необходимо убедиться в наличии или отсутствии в динамике среднесуточного объема грузоперевозок основной тенденции. Это можно сделать, применив ко всем тридцати шести уровням метод серий. Однако уже при построчном рассмотрении данных таблицы 10.17 видно, что в изменении уровней одноименных месяцев тенденции нет. Следовательно, весь ряд динамики также не имеет основной тенденции.
Исходные данные представлены за ряд лет, поэтому, учитывая отсутствие основной тенденции, расчет индексов сезонности проведем по формуле
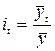 .
.
Так как грузооборот – это интервальный показатель, то средние значения уровней за одноименные месяцы рассчитаем по формуле среднюю арифметическую простую:
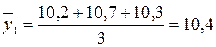 тыс. т;
тыс. т; 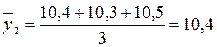 тыс. т;
тыс. т;
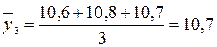 тыс. т;
тыс. т; 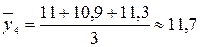 тыс. т;
тыс. т;
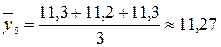 тыс. т;
тыс. т; 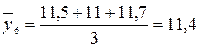 тыс. т;
тыс. т;
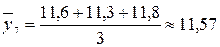 тыс. т;
тыс. т; 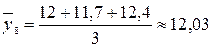 тыс. т;
тыс. т;
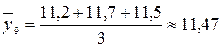 тыс. т;
тыс. т; 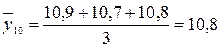 тыс. т;
тыс. т;
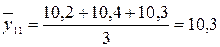 тыс. т;
тыс. т; 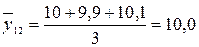 тыс. т;
тыс. т;
Поскольку в разных месяцах содержится различное число суток, то при расчете среднесуточного уровня грузоперевозок за три года на основе усреднения его значений для одноименных месяцев необходимо использовать формулу среднюю арифметическую взвешенную:
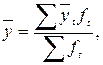
где 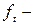 число суток в месяце с номером
число суток в месяце с номером 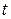 .
.
Тогда:
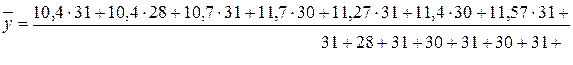
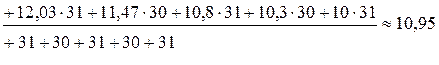 тыс. т.;
тыс. т.;
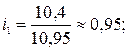
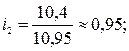
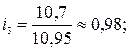
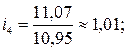
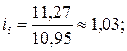
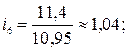
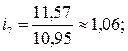
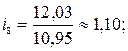
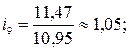
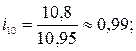
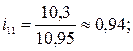
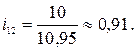
 На основе рассчитанных индексов сезонности построим сезонную волну (рис. 10.1).
На основе рассчитанных индексов сезонности построим сезонную волну (рис. 10.1).
Рис. 10.1
Из графика видно, что в изменении уровней среднесуточного объема грузоперевозок присутствуют ярко выраженные сезонные колебания. В апреле-сентябре уровень грузоперевозок выше среднегодового значения (уровень 100 %), в январе-марте и октябре-декабре – ниже среднего.
В целом грузоперевозки возрастают в летний период и убывают в зимний. При этом минимальный уровень наблюдается в декабре, максимальный – в августе. В осенне-весенние периоды объем перевозок приближается к среднему значению.
· Метод гармонического анализа сезонных колебаний уровней ряда динамики.
При гармоническом анализе сезонную составляющую изменения уровней рассматривают как результат действия совокупности гармонических колебаний и представляют в виде гармонического ряда Фурье:
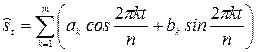 ,
,
где:
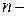 число уровней ряда динамики (число периодов или моментов времени);
число уровней ряда динамики (число периодов или моментов времени);
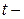 условный номер периода (момента) времени (
условный номер периода (момента) времени ( 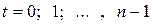 );
);
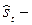 теоретические значения сезонных отклонений уровней от основной тенденции, а при ее отсутствии – от среднего уровня ряда динамики;
теоретические значения сезонных отклонений уровней от основной тенденции, а при ее отсутствии – от среднего уровня ряда динамики;
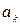 ,
, 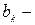 параметры
параметры 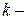 ой гармоники;
ой гармоники;
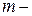 число гармоник.
число гармоник.
Для определения параметров 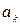 и
и 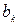 используют метод наименьших квадратов, который позволяет рассчитать эти параметры по формулам:
используют метод наименьших квадратов, который позволяет рассчитать эти параметры по формулам:
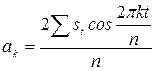 ;
; 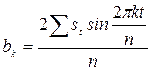 ,
,
где 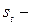 фактическое значение сезонного отклонения уровня за период
фактическое значение сезонного отклонения уровня за период 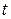 от соответствующего ему уровня основной тенденции, а при ее отсутствии – от среднего значения сезонных уровней.
от соответствующего ему уровня основной тенденции, а при ее отсутствии – от среднего значения сезонных уровней.
Пример 10.12. В таблице 10.18 представлены данные о динамике ежемесячного объема продаж молока в отчетном году на сельскохозяйственных рынках города.
Таблица 10.18
| Номер месяца | ||||||||||||
| Объем продаж, т |
Сформулируем математическую модель сезонных колебаний ежемесячного объема продаж молока на основе первой гармоники ряда Фурье.
Решение.
Искомая модель имеет вид
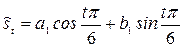 при
при 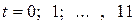 .
.
Прежде чем искать ее параметры, проверим наличие или отсутствие в ряду динамики основной тенденции методом серий. Для этого преобразуем ряд динамики в ряд распределения:
{28; 29; 29; 30; 34; 35; 35; 40; 43; 45; 54; 67}.
Определим медиану сформированного ряда распределения:
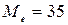 т.
т.
Заменим исходные уровни 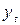 на тип А при
на тип А при 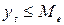 и B при
и B при 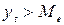 .
.
В результате:
{A; В; В; В; В; A; А; А; B; А; А; А}.
Таким образом, число серий R = 5. Оно находится в интервале 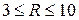 (см. пример 10.4). Из этого следуют, что в рассматриваемом ряду динамики основной тенденции нет, и сезонные колебания уровней необходимо рассматривать относительно среднего уровня ряда.
(см. пример 10.4). Из этого следуют, что в рассматриваемом ряду динамики основной тенденции нет, и сезонные колебания уровней необходимо рассматривать относительно среднего уровня ряда.
Для расчета параметров искомой модели заполним таблицу 10.19.
Вначале рассчитаем средний уровень исследуемого ряда динамики. Этот ряд является интервальным с равноотстоящими уровнями, поэтому средний уровень равен
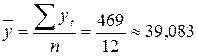 т.
т.
Таблица 10.19
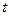
| 
| 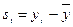
| 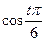
| 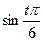
| 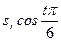
| 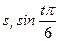
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| -9,083 | 1,000 | 0,000 | -9,083 | 0,000 | ||
| 0,917 | 0,866 | 0,500 | 0,794 | 0,459 | ||
| 3,917 | 0,500 | 0,866 | 1,959 | 3,392 | ||
| 14,917 | 0,000 | 1,000 | 0,000 | 14,917 | ||
| 27,917 | -0,500 | 0,866 | -13,959 | 24,176 | ||
| -10,083 | -0,866 | 0,500 | 8,732 | -5,042 | ||
| -4,083 | -1,000 | 0,000 | 4,083 | 0,000 | ||
| -5,083 | -0,866 | -0,500 | 4,402 | 2,542 | ||
| 5,917 | -0,500 | -0,866 | -2,959 | -5,124 | ||
| -4,083 | 0,000 | -1,000 | 0,000 | 4,083 | ||
| -10,083 | 0,500 | -0,866 | -5,042 | 8,732 | ||
| -11,083 | 0,866 | -0,500 | -9,598 | 5,542 | ||
| Итого | – | – | – | -20,670 | 53,676 |
Затем рассчитаем параметры первой гармоники ряда Фурье:
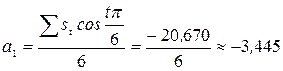 ;
;
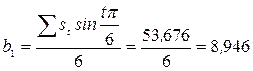 .
.
Таким образом, для условных значений номера месяца 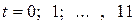 изменение уровней ежемесячного объема продаж молока с учетом сезонных колебаний описывается уравнением
изменение уровней ежемесячного объема продаж молока с учетом сезонных колебаний описывается уравнением
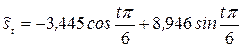 .
.
Обычно перебирают различные варианты уравнения сезонных отклонений ( 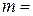 1; 2; ...). Делают это до тех пор, пока не получат приемлемые результаты с точки зрения адекватности уравнения фактическим данным, ориентируясь на значение остаточной дисперсии
1; 2; ...). Делают это до тех пор, пока не получат приемлемые результаты с точки зрения адекватности уравнения фактическим данным, ориентируясь на значение остаточной дисперсии
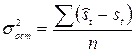 .
.
Индексы сезонности и уравнение сезонных отклонений могут быть использованы в качестве уточнения прогнозируемых уровней, рассчитываемых по уравнению тренда.
Дата добавления: 2022-07-20; просмотров: 217;











