Матрица питательности
| Питательное вещество | Продукт | |||
| F1 | F2 | … | Fn | |
| N1 | α11 | α12 | … | α1n |
| N2 | α21 | α22 | … | α2n |
| … | … | … | … | … |
| Nm | αm1 | αm2 | … | αmn |
Предположим, что диетолог уже выбрал диету, т.е. определил, что человек должен за месяц потреблять η1 кг продукта F1,..., ηn кг продукта Fn. Полное количество питательного вещества N1 будет
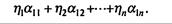
По условию требуется, чтобы его, по крайней мере, хватило
η1α11 + η2 α12 +…+ ηn α1n ≥ γ1
Точно то же и для остальных веществ. В целом
η1αi1 + η2 αi2 +…+ ηn αin ≥ γi (i = 1, 2,… m)
Эти условия определяют наличие минимума необходимых питательных веществ. Диета, для которой выполнены условия (7.78) - допустимая диета. Предположим, что из всех допустимых диет должна быть выбрана самая дешевая. Пусть πi - цена 1 кг продукта Fi. Полная стоимость диеты, очевидно,
S = π1η1 + π2η2 +… + πnηn.(7.79)
Таким образом, мы пришли к задаче: найти неотрицательное решение η1, …, ηn системы неравенств (7.78), минимизирующее выражение (7.79).
В примерах, приведенных выше. имеется нечто общее. Каждый из них требует нахождения наиболее выгодного варианта в определенной экономической ситуации. С чисто математической стороны в каждой задаче требуется найти значение нескольких неизвестных так, чтобы
1) все эти значения были неотрицательны;
2) удовлетворяли системе линейных уравнений или линейных неравенств;
3) при этих значениях некоторая линейная функция имела бы минимум (или максимум). Таким образом, линейное программирование - это математическая дисциплина, изучающая методы нахождения экстремального значения линейной функции нескольких переменных при условии, что последние удовлетворяют конечному числу линейных уравнений и неравенств. Запишем это с помощью формул: дана система линейных уравнений и неравенств.
Запишем это с помощью формул: дана система линейных уравнений и неравенств
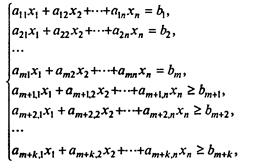 (7.80)
(7.80)
и линейная функция
f = c1x1 + c2x2 + … + cnxn(7.81)
Требуется найти такое неотрицательное решение
x1 ≥ 0, x2 ≥ 0, …, xn ≥ 0
системы (7.80), чтобы функция f принимала наименьшее (или наибольшее) значение.
Условия (7.80) называют ограничениями данной задачи, а функцию f - целевой функцией (или линейной формой). В приведенных выше примерах ограничения имели вид не уравнений, а неравенств. Заметим, что ограничения в виде неравенств всегда можно свести к системе в виде равенств (способом введения добавочных неизвестных).
Так, для неравенства
ai1x1 + ai2x2 + … + ainxn ≥ bi
вводя добавочное неизвестное xn +1, получаем
xn+1 = ai1x1 + ai2x2 + … + ainxn - bi
Потребовав его неотрицательности наряду с остальными неизвестными, получим, что условие xn + 1 ≥ 0 превращает (7.84) в (7.83). Введя по отдельному дополнительному неизвестному для каждого из неравенств, получим систему уравнений, равносильную исходной системе неравенств. Пример. Дана система неравенств
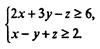
Сведем ее к системе уравнений. Получим
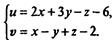
После оптимизации значениями дополнительных неизвестных следует пренебречь.
СИМПЛЕКС-МЕТОД
Для решения ряда задач линейного программирования существуют специальные методы. Есть, однако, общий метод решения всех таких задач. Он носит название симплекс-метода и состоит из алгоритма отыскания какого-нибудь произвольного допустимого решения и алгоритма последовательного перехода от этого решения к новому допустимому решению, для которого функция f изменяется в нужном направлении (для получения оптимального решения).
Пусть система ограничений состоит лишь из уравнений
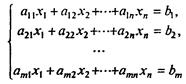
и требуется отыскать минимум линейной функции (7.81). Для отыскания произвольного опорного решения приведем (7.85) к виду, в котором некоторые r неизвестных выражены через остальные, а свободные члены неотрицательны (как это сделать - обсудим позднее):
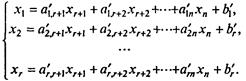
Неизвестные x1, x2, ..., xr - базисные неизвестные, набор {x1, x2, ..., xr} называется базисом, а остальные неизвестные {xr+1, xr+2, ..., xn} - свободные. Подставляя (7.86) в (7.81), выразим функцию
f через свободные неизвестные:
f = c0 + c'r+1xr+1 + c'хr+2 +…+ с'nxn.
Положим все свободные неизвестные равными нулю:
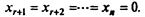
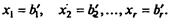
Полученное таким образом допустимое решение
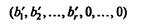
отвечает базису x1, х2, ..., xr, т.е. является базисным решением. Допустим для определенности, что мы ищем минимум f. Теперь нужно отданного базиса перейти к другому с таким расчетом, чтобы значение линейной функции f при этом уменьшилось. Проследим идею симплекс-метода на примере.
Пример 1. Дана система ограничений

x1 – 3x2 + 5x3 – x4 = 2
x1 + x2 + x3 + x4 = 4
Требуется минимизировать линейную функцию f = х2 – x3. В качестве свободных переменных выберем х2 и х3. Тогда данная система ограничений преобразуется к виду
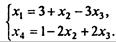
Таким образом, базисное решение (3, 0, 0, 1). Так как линейная функция уже записана в свободных неизвестных, то ее значение для данного базисного решения f = 0. Для уменьшения этого значения можно уменьшить x2 или увеличить x3. Но x2 в данном базисе равно нулю и потому его уменьшать нельзя. Попробуем увеличить x3. Первое из уравнений имеет ограничение x3 = 1 (из условия x1 ≥ 0), второе - не дает ограничений. Далее, берем x3 = 1, х2 не меняем и получаем новое допустимое решение (0, 0, 1, 3), для которого f = -1 - уменьшилось. Найдем базис, которому соответствует это решение (он состоит, очевидно, из переменных x3, x4). От предыдущей системы ограничений переходим к новой:
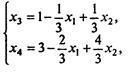
а форма в новых свободных переменных имеет вид
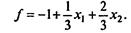
Теперь попробуем повторить предыдущую процедуру. Для уменьшения f надо уменьшить либо x1, либо x2, но это невозможно, так как в этом базисе x1 = 0, x2 = 0.
Таким образом, данное базисное решение является оптимальным, и minf= -1 при x1 = 0, x2 = 0, x3 = 1, x4 = 3.
Приведем алгоритм симплекс-метода в общем виде. Обычно все вычисления по симплекс-методу сводят в стандартные таблицы.
Запишем систему ограничений в виде
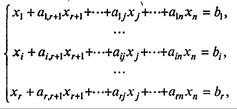 (7.90)
(7.90)
а функцию f
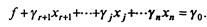 (7.91)
(7.91)
Тогда очередной шаг симплекс-процесса будет состоять в переходе от старого базиса к новому таким образом, чтобы значение линейной функции, по крайней мере, не увеличивалось.
Данные о коэффициентах уравнений и линейной функции занесем в табл. 7.12.
Таблица 7.12
Симплекс-таблица
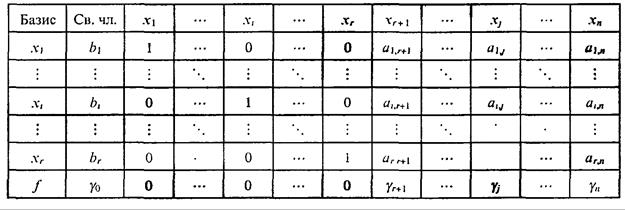
Сформулируем алгоритм симплекс-метода применительно к данным, внесенным в табл. 7.12.
1. Выяснить, имеются ли в последней строке таблицы положительные числа (γ0 не принимается во внимание). Если все числа отрицательны, то процесс закончен; базисное решение (b1, b2, .... br, 0, ..., 0) является оптимальным; соответствующее значение целевой функции f = γ0. Если в последней строке имеются положительные числа, перейти к п.2.
2. Просмотреть столбец, соответствующий положительному числу из последней строки, и выяснить, имеются ли в нем положительные числа. Если ни в одном из таких столбцов положительных чисел нет, то оптимального решения не существует. Если найден столбец, содержащий хотя бы один положительный элемент (если таких столбцов несколько, взять любой из них), пометить этот столбец и перейти к п. 3.
3. Разделить свободные члены на соответствующие положительные числа из выделенного столбца и выбрать наименьшее частное. Отметить строку таблицы, соответствующую наименьшему частному. Выделить разрешающий элемент, стоящий на пересечении отмеченных строки и столбца. Перейти к п. 4.
4. Разделить элементы выделенной строки исходной таблицы на разрешающий элемент (на месте разрешающего элемента появится единица). Полученная таким образом новая строка пишется на месте прежней в новой таблице. Перейти к п. 5.
5. Каждая следующая строка новой таблицы образуется сложением соответствующей строки исходной таблицы и строки, записанной в п. 4. которая предварительно умножается на такое число, чтобы в клетках выделенного столбца при сложении появились нули. На этом процесс заполнения новой таблицы заканчивается, и происходит переход к п. 1.
Таким образом, используя алгоритм симплекс-метода применительно к симплекс-таблице, мы можем найти оптимальное решение или показать, что его не существует. Результативность симплекс-метода гарантируется следующей теоремой (приведем ее без доказательства): если существует оптимальное решение задачи линейного программирования, то существует и базисное оптимальное решение. Это решение может быть получено через конечное число шагов симплекс-методом, причем начинать можно с любого исходного базиса.
Ранее мы предполагали, что если система ограничений задана в виде (7.85),топеред первым шагом она уже приведена к виду (7.86), где bi ≥ 0 (i = 1, 2, ..., r). Последнее условие необходимо для использования симплекс-метода. Рассмотрим вопрос об отыскании начального базиса.
Один из методов его получения - метод симплексного преобразования.
Прежде всего проверяем, есть ли среди свободных членов отрицательные. Если свободные члены не являются числами неотрицательными, то добитьсяих неотрицательности можно несколькими способами:
1) умножить уравнения, содержащие отрицательные свободные члены, на-1;
2) найти среди уравнений, содержащих отрицательные свободные члены, уравнение с максимальным по абсолютной величине отрицательным свободным членом и затем сложить это уравнение со всеми остальными, содержащими отрицательные свободные члены, предварительно умножив его на-1.
Затем, используя действия, аналогичные указанным в пп. 3 - 5 алгоритма симплекс-метода, совершаем преобразования исходной таблицы до тех пор, пока не получим неотрицательное базисное решение.
Пример 2. Найти исходное неотрицательное базисное решение системы ограничений
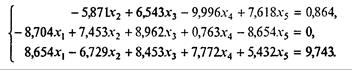
Так как условие неотрицательности свободных членов соблюдается, приступим к преобразованиям исходной системы, записывая результаты в таблицу. Согласно алгоритму просматриваем первый столбец. В этом столбце имеется единственный положительный элемент a31. Делим на 8,654 все коэффициенты и свободный член третьей строки, после чего умножаем каждый коэффициент на 8,704 и складываем с соответствующими коэффициентами второй строки. Первая строка преобразований не требует, так как коэффициент при неизвестном x1 равен нулю. В результате получаем
| 0,00000 0,00000 1,00000 | -5,87100 0,68512 -0,77756 | 6,54300 17,46384 0,97677 | -9,99600 8,57990 0,89808 | 7,61800 -3,19062 0,62769 | 0,86400 9,79929 1,11584 |
Продолжая просматривать второй столбец и совершая аналогичные преобразования, имеем
| 0,00000 0,00000 1,00000 | 0,00000 1,00000 0,00000 | 156,19554 25,49013 20,79687 | 63,52761 12,52318 10,63560 | -19,72328 -4,65701 -2,99341 | 84,83688 14,30299 12,24727 |
И, наконец, на третьем шаге находим исходный базис. Его образуют неизвестные x1, x2, x3. Неизвестные x4, х5 являются свободными:
| 0,00000 0,00000 1,00000 | 0,00000 1,00000 0,00000 | 1,00000 0,00000 0,00000 | 0,40672 2,15588 2,17713 | -0,12627 -1,43829 -0,36733 | 0,54315 0,45815 0,95155 |
При решении задачи линейного программирования целесообразно использование компьютера. В этом случае можно составить программу, решающую задачу. Учитывая,что программирование довольно трудоемко, можно посоветовать воспользоваться для оформления результатов расчетов табличным процессором. Кроме того, если получившаяся модель задачи слишком громоздка, можно воспользоваться математическими пакетами, которые позволяют получить решение задачи линейного программирования. И, наконец, еще один возможный вариант применения компьютеров - комбинирование всех вышеуказанных способов.
Контрольные вопросы и задания
1. Приведите примеры задач, приводящих к общей постановке задачи линейного программирования.
2. Сформулируйте задачу линейного программирования.
3. Сколько решений может иметь задача линейного программирования?
4. По каким причинам может отсутствовать решение задачи линейного программирования?
5. Каким образом неравенства из системы ограничений можно заменить уравнениями? Как задачу отыскания максимума линейной формы свести к задаче отыскания минимума?
6. Необходимо ли учитывать при записи решения дополнительные неизвестные, вводимые при переходе от неравенств к уравнениям?
7. Как найти начальный базис?
8. Сформулируйте алгоритм симплекс-метода.
9. Сформулируйте теорему о конечности алгоритма симплекс-метода.
10. Найдите максимум функции z = 4x1 +3x2 (xi ≥ 0) при условии
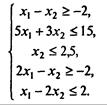
11. Для откорма крупного рогатого скота используется два вида кормов b1 и b2, в которые входят питательные вещества а1, a2, a3 и а4. Содержание количеств единиц питательных веществ в одном килограмме каждого корма, стоимость одного килограмма корма и норма содержания питательных веществ в дневном рационе животного представлены в таблице. Составьте рацион при условии минимальной стоимости.
| Питательные вещества | Вид кормов | Норма содержания питательного вещества | |
| b1 | b2 | ||
| a1 | |||
| a2 | |||
| a3 | |||
| a4 | |||
| Стоимость 1 кгкорма, руб. |
12. Трикотажная фабрика использует для производства свитеров и кофточек чистую шерсть, силон и нитрон, запасы которых составляют, соответственно, 800, 400 и 300 кг. Количество пряжи (кг), необходимое для изготовления 10 изделий, а также прибыль, получаемая от их реализации, приведены в таблице. Составьте план производства изделий, обеспечивающий получение максимальной прибыли.
| Вид сырья в пряже | Затраты пряжи на 10 шт., кг | |
| Свитер | Кофточка | |
| Шерсть | ||
| Силон | ||
| Нитрон | ||
| Прибыть, руб. |
13. При подкормке посевов необходимо внести на 1 га почвы не менее 8 единиц химического вещества A, не менее 21 единиц химического вещества В и не менее 16 единиц химического вещества С. Фермер закупает комбинированные удобрения двух видов I и II. В таблице указано содержание количества единиц химического вещества в 1 кг каждого вида удобрений и цена 1 кг удобрений. Определите потребность фермера в удобрениях I и II вида на 1 га посевной площади при минимальных затратах на их приобретение.
| Химические вещества | Содержание химических веществ в 1 кг удобрения | |
| I | II | |
| А | ||
| В | ||
| С | ||
| Цена 1 кг удобрения, руб |
14. На звероферме выращивают черно-бурых лис и песцов. Для обеспечения нормальных условий их выращивания используют три вида кормов. Количество корма каждого вида, которое должны получать животные, приведено в таблице. В ней также указаны общее количество корма каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца. Составьте план выращивания животных, обеспечивающий максимальную прибыль.
| Вид корма | Количество единиц корма, которое ежедневно должны получать | Общее количество корма | |
| Лисица | Песец | ||
| III | |||
| Прибыль от реализации одной шкурки, руб |
Дополнительная литература к главе 7
1. Араманович И. Г., Левин В. И. Уравнения математической физики. - М.: Наука, 1969.
2. Акулич И. Л. Математическое программирование в примерах и задачах. - М.: Высшая школа, 1993.
3. Беллман Р. Математические методы в медицине: Пер. с англ. - М.: Мир, 1987.
4. Белошапка В К Информационное моделирование в примерах и задачах. -Омск: Из-во ОГПИ, 1992.
5. Бигон М., Харпер Дж., Таунсенд К. Экология. Особи, популяции и сообщества: Пер. с англ. В двух книгах. Кн. 1. - М.: Мир, 1989.
6. Воеводин В. В. Численные методы алгебры. - М.: Наука, 1966.
7. Гнеденко Б. В. Курс теории вероятностей. - М.: Наука, 1965.
8. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслуживания. -М.: Наука, 1966.
9. Горстко А. Б. Познакомьтесь с математическим моделированием. - М.: Знание, 1991.
10. Горстко А. Б., Угольницкий Г. А. Введение в моделирование эколого-зкономических систем. - Ростов: Из-во РГУ, 1990.
11.Гулд X., Тобочник Я. Компьютерное моделирование в физике: Пер. с англ. Т. 1, 2.-М.: Мир, 1990.
12. Демидович Б. П., Марон И. А.Основы вычислительной математики. - М.: Наука,1970.
13. Заварыкин В.М., Житомирский В. Г,. Лапчик М.П. Численные методы. - М.: Просвещение,1990.
14. Зайденберг А. П., Павлович Е.С. Законы распределения случайных величин. -Омск: Изд-во ОГПИ, 1971.
15. Зуховицкий СИ., Авдеева Л. И. Линейное и выпуклое программирование. - М.:
Наука,1967.
16. Кондаков В.М. Математическое программирование. Элементы линейной алгебры и линейного программирования - Пермь: Из-во ПГУ, 1992.
17. Марчук Г.И. Математическое моделирование в иммунологии. - М.: Наука, 1991.
18. Математическое моделирование: Пер. с англ. / Под ред. Дж. Эндрюса, Р. Мак-Лоуна. - М.: Мир, 1979.
19. Матюшкин-Герке А. Учебно-прикладные задачи в курсе информатики. Информатика и образование, № 3-4, 5-6, 1992.
20. Мигулин В. В., Медведев В. И., Мустель Е.Р., Парыгин В.Н. Основы теории колебаний. - М.: Наука, 1988.
21. Риклефс Р. Основы общей экологии: Пер. с англ. - М.: Мир, 1979.
22. Саати Т. Элементы теории массового обслуживания и ее приложения: Пер. с англ. - М.: Сов. радио, 1971.
23. Сайдашев А. А., Хеннер Е.К. Компьютер на уроке математики. - Пермь: Из-во ПГУ.1991.
24. Самарский А. А., Гулин А.В. Численные методы. - М.: Наука, 1989.
25. Стрелков С П. Введение в теорию колебаний. - М.: Наука, 1964.
26. Шеннон Р. Имитационное моделирование систем - искусство и наука: Пер. с англ. - М.: Мир, 1978.
27. Электронные вычислительные машины. / Под ред. АЯ.Соловьева. В 8 книгах. Книга 8. Решение прикладных задач. - М.: Высшая школа, 1987.
Дата добавления: 2020-02-05; просмотров: 753;











