Гамма-функция. Интеграл и производная дробного порядка
Неэлементарная гамма-функция определяется следующим несобственным интегралом, зависящим от параметра
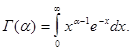 (1)
(1)
Убедимся, что интеграл (1) сходится для всех 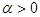 и действительно определяет функцию. Разобьем несобственный интеграл (1) на два несобственных интеграла
и действительно определяет функцию. Разобьем несобственный интеграл (1) на два несобственных интеграла 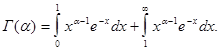 (2)
(2)
При 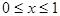 подынтегральная функция первого интеграла удовлетворяет следующему неравенству
подынтегральная функция первого интеграла удовлетворяет следующему неравенству 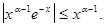 Т.к. интеграл
Т.к. интеграл 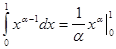 сходится при
сходится при 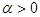 (и расходится при
(и расходится при 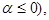 то по признаку сравнения первый несобственный интеграл в (2) сходится при
то по признаку сравнения первый несобственный интеграл в (2) сходится при 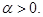 При
При 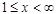 подынтегральную функцию второго несобственного интеграла (2) сравним с функцией
подынтегральную функцию второго несобственного интеграла (2) сравним с функцией 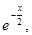 интеграл от которой
интеграл от которой 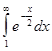 сходится.
сходится.
Используя правило Лопиталя, найдем предел 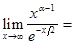
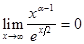 при любом
при любом 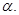 А это означает, что
А это означает, что 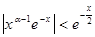
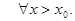 По признаку сравнения второй несобственный интеграл в (2) сходится.
По признаку сравнения второй несобственный интеграл в (2) сходится.
Итак, мы доказали, что интеграл (1) сходится и определяет гамма-функцию для всех 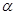 больших нуля. Можно доказать, что
больших нуля. Можно доказать, что 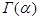 непрерывная и дифференцируемая сколько угодно раз при
непрерывная и дифференцируемая сколько угодно раз при 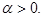 При
При 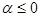 интеграл (1) расходится. Интегрируя (1) по частям, получим
интеграл (1) расходится. Интегрируя (1) по частям, получим
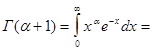
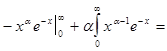
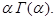 (3)
(3)
Если 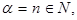 то используя формулу (3)
то используя формулу (3) 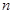 раз, получим
раз, получим
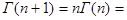
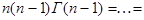
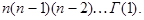
Из (1) видно, что 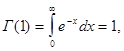 поэтому
поэтому
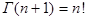
Перепишем (3) в виде
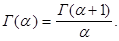 (4)
(4)
Из (4) видно, что 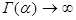 при
при 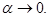
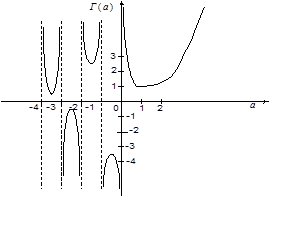
Формулу (4) используют, чтобы продолжить гамма-функцию на отрицательные значения 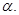 Действительно, если
Действительно, если 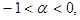 то
то 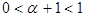 и правая часть (4) определена. Очевидно,
и правая часть (4) определена. Очевидно, 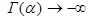 при
при 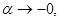
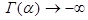 при
при 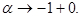 Зная значения при
Зная значения при 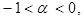 можно по формуле (4) вычислить значения функции
можно по формуле (4) вычислить значения функции 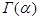 при
при 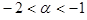 и т.д. (график гамма-функции см. на рис.).
и т.д. (график гамма-функции см. на рис.).
Интеграл (1), определяющий гамма-функцию для положительных значений a, можно аналитически продолжить на комплексную полуплоскость Rea > 0. Для аналитического продолжения гамма – функции в левую полуплоскость используется формула (4). В результате получим аналитическую функцию Г(a) во всей комплексной плоскости, исключая точки a = 0, -1, -2, ¼, в которых она имеет простые полюса.
Замечание.Если в формуле * (см. §6 гл.8, ч.I) факториал заменить на гамма-функцию (Г(n) = (n – 1)!), то можно определить интеграл от функции f(x) любой кратности a > 0 (в том числе и дробной) формулой
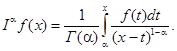 (5)
(5)
А поскольку интегрирование и дифференцирование – это две взаимно обратные операции, то можно определить и производную дробного порядка.
Чтобы найти производную от функции f(x) порядка a > 0, следует взять от нее интеграл порядка 1 – {a} ({a} – дробная часть a) и от полученного интеграла взять обычную производную порядка 1 + [a] = n ([a] – целая часть a), т.е.
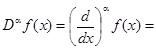
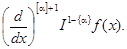 (6)
(6)
Определение дробной производной (6) можно записать иначе:
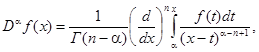 (7)
(7)
Достаточным условием существования производной порядка a является существование непрерывной производной порядка [a] функции f(x).
Пример.Найти производные порядка a = 1¤4 и a = 5¤4 от функции f(x) = x.
Решение.В нашем случае 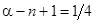 при a = 1¤4 и при a = 5¤4. Воспользуемся формулой (7) и вычислим интеграл
при a = 1¤4 и при a = 5¤4. Воспользуемся формулой (7) и вычислим интеграл 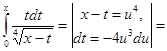
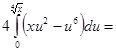
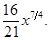
Согласно формуле (7)
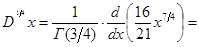
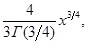
а 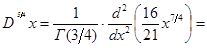
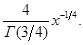
Упражнение.Найти 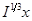 и
и 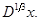
Понятие интеграла и производной порядка a можно распространить и на комплексные значения a, такие, что Rea > 0
Дельта-функция
В линейном 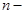 мерном пространстве тождественный (единичный) оператор
мерном пространстве тождественный (единичный) оператор 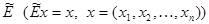 определяется единичной матрицей
определяется единичной матрицей 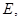 которую можно записать с помощью символа Кронекера
которую можно записать с помощью символа Кронекера
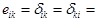
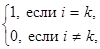

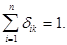 (1)
(1)
При этом 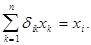 (2)
(2)
В функциональном пространстве по аналогии вводят интегральный единичный оператор, который можно записать с помощью так называемой дельта-функции 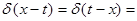
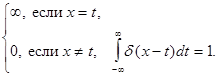 (3)
(3)
При этом 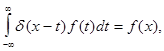 (4)
(4)
если 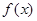 непрерывная в точке
непрерывная в точке 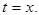
Дельта-функция может быть многими способами представлена в виде некоторого предела. Например,
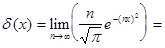
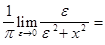
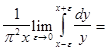
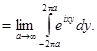 (5)
(5)
Приведем некоторые свойства 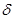 - функции.
- функции.
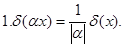
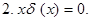
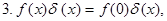
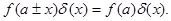
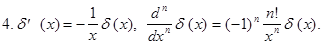
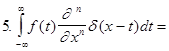
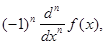
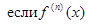 непрерывна.
непрерывна.
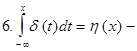 единичная функция Хевисайда.
единичная функция Хевисайда.
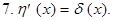
С введением 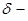 функции функции с разрывами первого рода становятся формально дифференцируемыми.
функции функции с разрывами первого рода становятся формально дифференцируемыми.
Пример 1.Найти производную функции 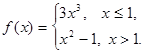
Решение.Функция 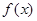 в точке
в точке 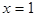 имеет скачок
имеет скачок 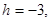 в остальных точках
в остальных точках 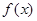 дифференцируемая. Поэтому
дифференцируемая. Поэтому
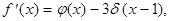 где
где 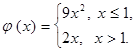
Пример 2.Тонкий материальный стержень, расположенный по оси 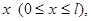 имеет линейную плотность
имеет линейную плотность 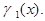 В точках
В точках 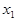 и
и 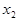 на него надеты тонкие диски, массы которых
на него надеты тонкие диски, массы которых 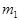 и
и 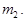 Записать выражение для общей линейной плотности стержня с дисками.
Записать выражение для общей линейной плотности стержня с дисками.
Решение. Используя 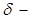 функцию, запишем
функцию, запишем
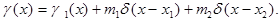
Общая масса, очевидно, запишется так:
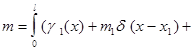
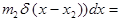
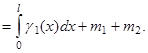
Дата добавления: 2020-02-05; просмотров: 905;











