Физические процессы в мембранах

Изучение структуры и функционирования биологических мембран имеет важное значение для медицины, так как многие патологические процессы в клетке связаны с нарушением функций мембран. Их площадь огромна. Площади достаточно для обеспечения многочисленных процессов, протекающих на мембранах, обеспечивающих жизнеспособность человека. Общая площадь мембран в органах человека ‑ десятки тысяч квадратных метров.

а) Функции мембран:

– Механическое разделение.

– Транспортная функция.

– Селективный барьер.

– Рецепция (распознавание).

– Распространение нервного импульса.

– Матричная, для удержания белков, ферментов.

Основу мембраны составляет двойной фосфолипидный слой. Липиды (вещества на основе жирных кислот) состоят из полярной головы и двух неполярных углеводородных хвостов. Головы – гидрофильны (притягивают молекулы воды). Хвосты – гидрофобны (не взаимодействуют с водой). Хвосты обращены внутрь бимолекулярного слоя (рис. 56). Гидрофильные головы взаимодействуют с внешними белковыми слоями и молекулами воды вне и внутри клетки.

Липиды и белки в бислое могут перемещаться достаточно быстро внутри слоя вдоль плоскости мембраны (Латеральная диффузия) и очень медленно между двумя монослоями поперек мембраны. На одну молекулу белка приходится 70‑90 молекул липидов.

75‑80 % поверхности мембраны покрывают белковые молекулы (липопротеиды), которые придают ей эластичность и устойчивость к механическим повреждениям. Этот слой играет также роль носителя электрического заряда.

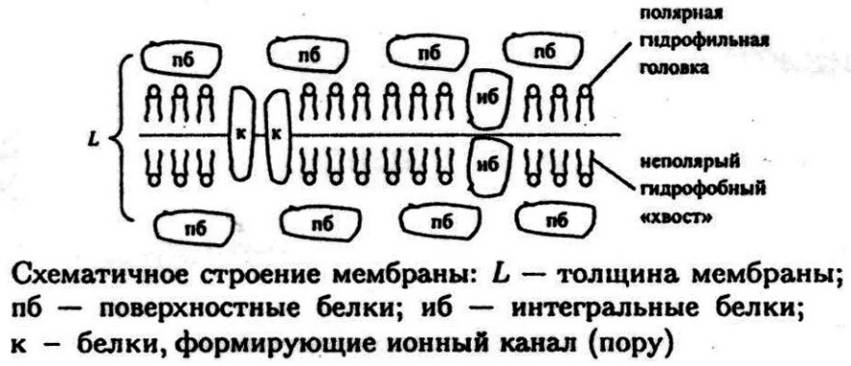
Рис. 56.Схематичное строениемембраны: L – толщина мембраны;

пб – поверхностные белки; иб – интегральные белки;

к – белки, формирующие ионный канал (пору)

Интегральные белки – они ответственны за избирательную проницаемость клеточной мембраны. Их диаметр 0,35‑0,8 нм. Их количество невелико (в эритроцитах площадь этих каналов составляет всего 0,06 %). Некоторые из этих белков функционируют как ионные насосы (на рис. 56. обозначены к) и регулируют электрохимическую систему возбуждения клетки. Стенки каналов обладают электрическим зарядом.

б) Модели мембран.

На моделях мембран изучают их свойства.

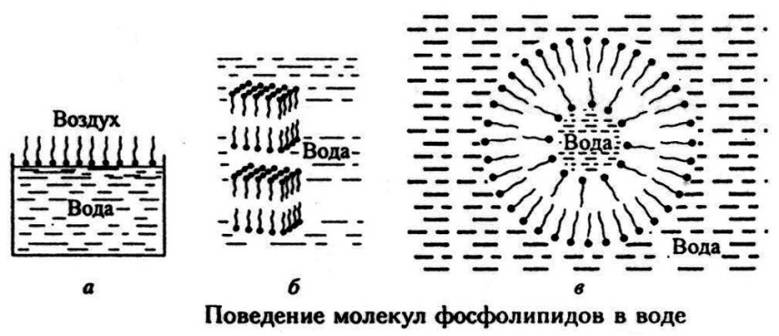
Рис. 57.Поведение молекул фосфолипидов в воде

Монослой (рис. 57 а). Молекулы фосфолипидов помещены на границу раздела вода – воздух. Пока молекул немного они располагаются на поверхности, прильнув головами к воде.

Плоский бислой (рис. 57 б). Если в водном растворе липидных молекул много, то эти молекулы собираются так, чтобы гидрофобные хвосты были закрыты от воды. Такая модель позволяет изучать ионную проницаемость, генерацию электрического потенциала на мембране.

Липосомы. Липидные бислои, имея большую протяженность, стремятся замкнуться сами на себя. При этом образуются фосфолипидные везикулы (пузыри) – липосомы (рис. 57 в).

Липосома практически лишена белков. В медицине липосомы используют для доставки лекарственных средств в определенные органы и ткани, приготавливая их в среде содержащей нужное вещество. Так готовят кремы, мази в дерматологии и косметологии.

в) Физические свойства мембран.

Плотность ρ = 800 кг/м³; Толщина 4‑13 нм; прочность: максимальная деформация составляет ~ 0,01 %; внутреннее давление в клетке не более 100 Па; модуль упругости 0,45 Па; вязкость 30‑100 мПа·с (как у растительного масла); поверхностное натяжение 0,03–3 мН·м^–1; коэффициент проницаемости 25‑30 10^–4 см/с; электроемкость 1 см² ~ 0,5–1,3 мкФ; напряженность поля 20 10⁶ В/м; диэлектрическая проницаемость
ε = 2,0–2,2 для фосфолипидной области; ε = 10–20 для
гидрофильной области; электрическое сопротивление
1 см² ~ 10²–10⁵ Ом (это в десятки миллионов раз больше сопротивления внеклеточной жидкости или цитоплазмы); показатель преломления n = 1,55; состояние мембраны – жидкокристаллическое.

Уравнение Нернста-Планка

Перенос молекул через мембрану осуществляется диффузией и описывается уравнением Фика (уравнение диффузии):

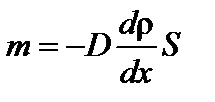или ;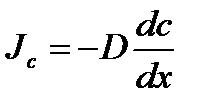

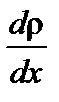‑ градиент плотности; 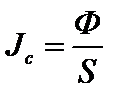‑ плотность потока вещества; ‑ градиент концентрации; D – коэффициент диффузии; 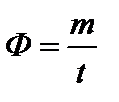– поток вещества – это масса вещества, проходящего через площадку S за единицу времени.

Перенос ионов происходит под действием электрического поля. Сила, действующая на ион со стороны поля: f₀=qE; q=Ze
(Z – валентность); q – заряд иона; E – напряженность поля;
e – заряд электрона; – градиент потенциала. Тогда 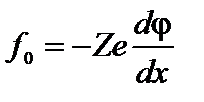; Сила, действующая на ионы в одном моле 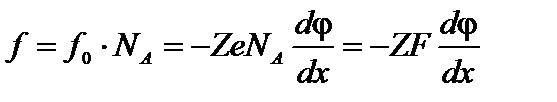; 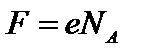‑ постоянная Фарадея. Средняя скорость движения ионов, в которой учитываются силы сопротивления, определяется как:

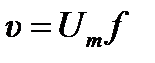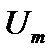, – подвижность иона.

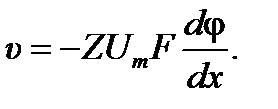
Найдем поток вещества, переносимый ионами, через элемент площади S. Выделим в электролите цилиндр (рис. 58).

Рис. 58.

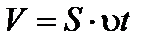Объем его ; За время t все ионы, находящиеся в цилиндре пройдут через площадку S. Тогда 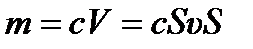; здесь c – концентрация ионов. 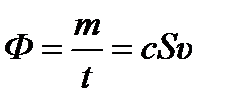или .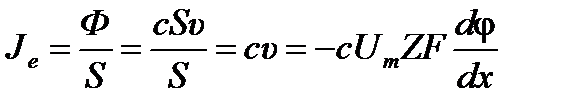

В общем случае перенос частиц связан и с градиентом концентрации и с действием электрического поля, т.е. ;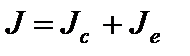

Это уравнение Нернста–Планка (электродиффузионное уравнение).