И последовательных схемах

Как было сказано ранее (Часть 2) при разработке цифрового устройства на его первоначальной стадии используют логическую модель, которая описывает идеальную схему и не учитывает задержек, которые возникают в схеме. Это может привести к тому, что в некоторый момент времени основные аксиомы алгебры логики (А)*(-А)=0 и (А)+(-А)=1 не подтверждаются.

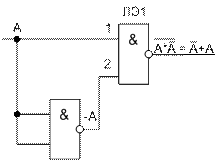
На Рис.3.14 (а) приведена схема реализующая выражение (А)+(-А) на элементах И-НЕ с использованием теоремы Де-Моргана.

Из временной диаграммы на Рис.3.14 (в) видно, что на выходе имеется ложный сигнал уровня «0», длительность которого определяется величиной задержки в ЛЭ1 (инвертор).

Подобная ситуация может возникнуть тогда, когда при изменении входного сигнала выходной остается постоянным.

а)	б)
Рис.3.14. Схема реализующая выражение (А)+(-А) (а), диаграмма работы (б)

Возможность появления состязаний требует, чтобы были предприняты меры исключающие вызванные ими сбои.

Основным средством позволяющим исключить последствия состязаний является стробирование. Под стробированием понимают выделение из информационного сигнала той его части которая свободна от ложных сигналов вызванных состязаниями.

Всякая комбинационная логическая цепь заканчивается запоминающим элементом (триггером). Поэтому стробирование целесообразно вводить на входе в триггер.

Триггерные схемы, входные сигналы которого стробируются специальными периодическими импульсами, называются синхронными.

Введение синхронизации позволяет также создать условия для одновременного изменения состояний многих триггерных схем (синхронная работа всего устройства).