Модель простой линейной регрессии

Если функция регрессии линейная, то говорят о линейной регрессии. Линейная регрессия находит весьма широкое применение в эконометрике в связи с четкой экономической интерпретации ее параметров.

Кроме того, построенное линейное уравнение может служить начальной точкой эконометрического анализа.

Простая линейная регрессия представляет собой линейную функцию между условным математическим ожиданием зависимой переменной 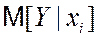и одной зависимой переменной X (x_i – значения зависимой переменной в i-ом наблюдении):

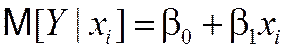. (5)

Для отражения того факта, что каждое индивидуальное значение y_i отклоняется от соответствующего условного математического ожидания, необходимо ввести в соотношение (5) случайное слагаемое ε_i:

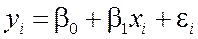. (6)

Это соотношение называется теоретической линейной регрессионной моделью; β₀ и β₁ – теоретическими коэффициентами регрессии. Таким образом, индивидуальные значения y_i представляют в виде двух компонент – систематической ( 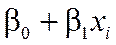) и случайной (ε_i). В общем виде теоретическую линейную регрессионную модель будем представлять в виде

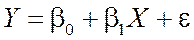. (7)

Основная задача линейного регрессионного анализа состоит в том, чтобы по имеющимся статистическим данным для переменных X и Y получить наилучшие оценки неизвестных параметров β₀ и β₁.

По выборке ограниченного объема можно построить эмпирическое линейное уравнение регрессии:

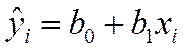, (8)

где 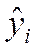– оценка условного математического ожидания 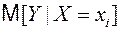, b₀ и b₁ – оценки неизвестных параметров β₀ и β₁, называемые эмпирическими коэффициентами регрессии. Следовательно, в конкретном случае

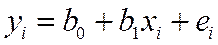, (9)

где отклонение e_i – оценка теоретического случайного отклонения ε_i.

Задача линейного регрессионного анализа состоит в том, чтобы по конкретной выборке (x_i,y_i) найти оценки b₀ и b₁ неизвестных параметров β₀ и β₁ так, чтобы построенная линия регрессии была бы наилучшей в определенном смысле среди всех других прямых.

Другими словами, построенная прямая 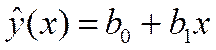должна быть «ближайшей» к точкам наблюдений по их совокупности.

Мерами качества найденных оценок могут служить определенные композиции отклонений e_i. Например, коэффициенты b₀ и b₁ эмпирического уравнения регрессии могут быть оценены исходя из условия минимизации функции потерь (loss function):

.

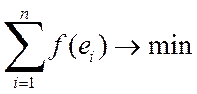Самым распространенным и теоретически обоснованным является метод нахождения коэффициентов, при котором минимизируется первая сумма. Он получил название метод наименьших квадратов (МНК).