Основные задачи регрессионного анализа

В силу неоднозначности корреляционной зависимости между Y и X, для изучения влияния независимой переменной на объясняемую переменную используют «усредненные» зависимости, т.е. изучают условное математическое ожидание M[Y|X=x] (математическое ожидание случайной величины, вычисленную в предположении, что переменная X приняла значение x) в зависимости от x.

Поскольку при различных значениях будут получаться различные значения условного математического ожидания, то мы будем иметь дело с некой функцией

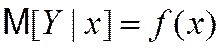, (1)

которая называется функцией регрессии Y на X.

Отметим, что реальные значения зависимой переменной Y не всегда совпадают с ее условными математическими ожиданиями и могут быть различными при одном и том же значении объясняющей переменной.

Поэтому связь между зависимой и объясняющей переменной обычно записывают в виде

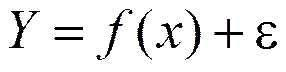, (2)

называемое теоретическим уравнением регрессии. Величину e обычно называют случайным отклонением (ошибкой, возмущением). Это слагаемое, которое, по существу, является случайной величиной и указывает на стохастическую суть зависимости.

Для определения параметров функции регрессии необходимо знать и использовать все значения переменных X и Y генеральной совокупности, что практически невозможно.

Основные задачи регрессионного анализа состоят в том, чтобы по имеющимся статистическим данным для переменных X и Y:

а) установить форму зависимости между переменными;

б) оценить функцию регрессии (т.е. получить наилучшие оценки неизвестных параметров, проверить статистические гипотезы о параметрах модели);

в) проверить, достаточно ли хорошо модель согласуется со статистическими данными (адекватность модели данным наблюдений);

г) оценить неизвестные значения зависимой переменной (сделать прогноз значений).

Используя выборочные данные можно построить так называемое эмпирическое уравнение регрессии:

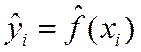, (3)

где 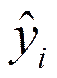– оценка условного математического ожидания , 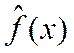– оценка функции регрессии.

Следовательно, в конкретном случае

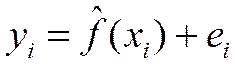, (4)

где отклонение e_i – оценка теоретического случайного отклонения ε_i. Эту величину также называют остатками (residuals).

Решений задачи построения качественного уравнения регрессии, соответствующего эмпирическим данным и целям исследования, является достаточно сложным и многоступенчатым процессом. Его можно разбить на три этапа:

1) выбор формулы уравнения регрессии (спецификация);

2) определение параметров выбранногоуравнения (параметризации);

3) анализ качества уравнения и поверка адекватности уравнения эмпирическим данным, совершенствование уравнения (верификации).

В случае парной регрессия выбор формулы обычно осуществляетсяпо графическому изображению реальных статистических данных в виде точек в декартовой системе координат, которое называется корреляционным полем (диаграммой рассеивания)(см., например, рис. 5.1).

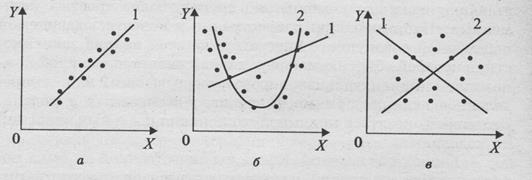
Рис. 1

На рис. 1 представлены три ситуации.

На графике 5.1, а взаимосвязь между Х и Y близка к линейной, и прямая 1 достаточнохорошо соответствуетэмпирическим точкам. Поэтому в данном случае в качестве зависимости между Х и Y целесообразно выбрать линейную функцию .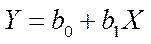

На графике 1, б реальная взаимосвязь между Х и Y, скорее всего, описывается квадратичной функцией 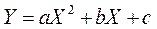(линия 2).

И какую бы мы ни провели прямую (например, линия I), отклонения точек наблюдений от нее будут существенными и неслучайными.

На графике 1, в явная взаимосвязь между Х и Y отсутствует. Какую бы мы ни выбрали форму связи, результаты ее спецификации и параметризации (определение коэффициентов уравнения) будут неудачными.

В частности, прямые 1 и 2, проведенные через центр «облака» наблюдений и имеющие противоположный наклон, одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной Y по значениям переменной X.

Более подробно вопросы спецификации, а также вопросы параметризациии верификации уравнения регрессии, будут обсуждены в следующих лекциях.