Методы прогнозирования паводков

В зависимости от аналитического подхода, используемого для разработки прогностической модели, методы прогнозирования паводков можно классифицировать следующим образом:
- методы, основанные на статистическом подходе;
- методы, основанные на механизме формирования и распространения паводков.

Методы прогнозирования в форме математических связей, разработанные с помощью исторических данных наблюдений и статистического анализа, широко использовались в прошлом. Они включают простые, эмпирически установленные связи рассматриваемой величины с некоторыми дополнительными параметрами и связи уровня воды с максимальными осадками.

Эти связи можно легко установить, и поэтому они чаще всего используются на начальном этапе формирования системы прогнозирования паводков. Использование искусственных нейронных сетей для прогнозирования стока в период паводков — это другой подход в моделировании, который в последнее время приобрел популярность.

Процедуры прогнозирования в возрастающей степени основываются на более полных физических описаниях основных гидрологических и гидравлических процессов. Во многих случаях, когда необходимы прогнозы расходов или уровней воды по длине реки, гидрологи используют модели типа «осадки-сток» совместно с моделями распространения паводочной волны.

Если осадки представлены в форме снега, применяются модели снеготаяния. Эти модели различаются по точности и сложности, занимая весь спектр от моделей, основанных на использовании индекса предшествующего увлажнения, до многопараметрических концептуальных моделей или моделей процессов.

Следуя за достижениями в сфере компьютерных технологий и телеметрии, прогностические модели становятся в последнее время более гибкими с точки зрения предоставления информации и возможности использования новых данных и накопленного опыта в режиме реального времени.

Существует много разновидностей этих основных категорий моделей, и большинство различается в зависимости от способа параметризации гидрологических процессов. Модели могут варьироваться от самых простых, построенных на статистической связи между осадками и стоком в сочетании с уравнением трансформации, до моделей, характеризуемых гораздо более высокой степенью сложности.

Гидрологические модели можно разделить на модели с сосредоточенными, распределенными и полураспределенными параметрами. Модели могут быть событийными или непрерывными. Если модель способна оценивать только конкретное событие, например пик паводка в результате шторма, то такая модель называется событийной. Непрерывная модель способна предсказывать весь гидрограф паводка за заданный интервал времени.

Требования при выборе модели включают следующие факторы:
- цели прогнозов и требования к ним;
- степень необходимой точности;
- наличие данных;

- наличие технических средств;
- наличие подготовленного персонала для разработки модели и ее оперативного использования;
- возможность модернизации модели.

За последние двадцать лет был сделан значительный прогресс в развитии методологии и улучшении производительности таких моделей. Однако производительность обычно изменяется в зависимости от моделируемых характеристик речного бассейна, наличия данных для калибровки и опыта работающего с моделью гидролога и его понимания этой модели.

Существует большое число общедоступных и запатентованных моделей для прогнозирования паводков. В главе 6 настоящего Руководства дается описание многих имеющихся на данный момент гидрологических моделей.

Статистический метод. Коэффициент корреляции характеризует линейную взаимосвязь между двумя переменными и широко применяется как математическое средство на первоначальном этапе многих гидрологических анализов.

Регрессия — это расширенный корреляционный подход, который обеспечивает получение формулы, по которой можно рассчитать желаемую переменную, например сезонный меженный сток, по данным одного или нескольких имеющихся в настоящее время наблюдений, например по максимальному уровню грунтовых вод в зимний период (см. Draper and Smith, 1966).

Формула для расчета коэффициента корреляции между двумя переменными х и у при длине ряда n имеет следующий вид:

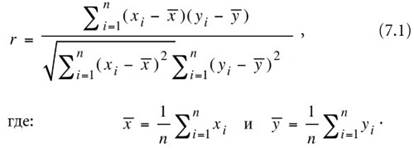
Отсутствие корреляции не означает отсутствие взаимосвязи, поскольку r является показателем только линейной связи и, например, четкая криволинейная зависимость не обязательно будет отражена в высоком значении величины r.

И наоборот, корреляционная связь между двумя переменными не означает их причиннообусловленную связь. Простой график с разбросом точек около прямой линии является графическим представлением корреляционной связи двух переменных и лежит в основе метода прогнозирования максимального уровня воды в реке (см. раздел 7.3.4, посвященный верификации прогнозов).

Если либо переменная х, либо переменная у имеют структуру временного ряда, особенно тренд, то перед установлением корреляционной зависимости необходимо принять меры по исключению этой структуры, и должна соблюдаться осторожность при проверке ее значимости. Методы временных рядов можно применять (см. раздел 7.5.3) тогда, когда предшествующие значения переменной, такой как расход реки, используются для прогнозирования значения той же самой переменной в определенный момент времени в будущем.

Подобным образом получили широкое распространение в гидрологии и уравнения регрессии. Их общий вид является следующим:

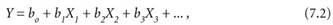
где X — текущие значения наблюденных переменных, а Y — будущее значение прогнозируемой переменной; b — показывает коэффициенты регрессии, рассчитанные по наблюденным значениям Y и X. Переменный X могут включать уровень или расход воды выше по течению реки, осадки, характеристики водосбора, температуру воздуха или сумму дождевых осадков за сезон. Переменная Y может характеризовать как минимальный, так и максимальный уровень воды.

Коэффициент множественной корреляции определяет степень достоверности связи. Другая мера соответствия — стандартная ошибка оценки — характеризует разброс точек относительно линии регрессии, построенной для обучающей выборки. Эта теория излагается во всех основных учебниках по статистике.

В некоторых случаях применение аппарата линейной регрессии приводит к неудовлетворительным результатам, и возникает необходимость в нормализации переменных X или Y. Мощный инструмент преобразования может применяться для преобразования Y в Y_T посредством следующих уравнений:

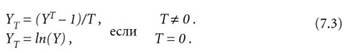
Эти числовые выражения охватывают степенное, логарифмическое и гармоническое преобразования на непрерывной шкале T. Подходящее значение T может быть найдено подбором, при котором уменьшается асимметрия, или графически при помощи диаграммы, как показано на рисунке II.7.4.

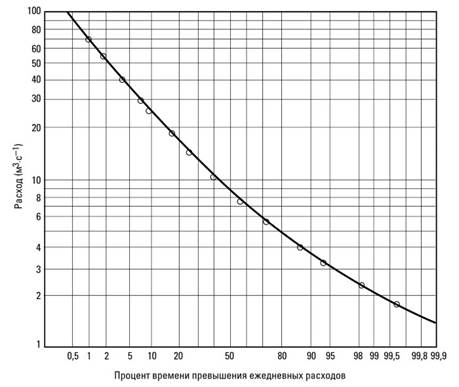
Рисунок II.7.4. Кривая продолжительности стока ежедневных расходов

Нелинейные связи можно также описать с помощью полиномов, например, вводя X_і X_і² или X_і³ в уравнение регрессии. С другой стороны, методы с использованием процедуры минимизации целевой функции открывают простой способ подбора параметров строго нелинейных уравнений. Выбор подходящего набора из большой совокупности переменных требует определенных навыков, в частности тщательного анализа разностей между наблюденными и рассчитанными величинами в обучающей выборке.

Обстоятельства, вызывающие появление больших остаточных отклонений, часто указывают на необходимость выполнения корректировок. Для исследования различных сочетаний переменных должны быть использованы преимущества компьютерной обработки и графического изображения остаточных отклонений.

Следует избегать полностью автоматизированного поиска и выбора процедур с использованием ступенчатого, поэтапного, прямого и обратного отбора выборок и оптимальных группировок переменных. Примеры применения регрессионных методов для различных задач прогнозирования даны в разделах 7.3.2.3 и 7.4.7.

Модели с использованием индекса влажности почвы. Индекс предшествующих осадков описан в разделе 6.3.2.2. Этот подход во многих странах является основным средством для оперативного прогнозирования. В качестве меры влияния на сток осадков, выпавших до выпуска прогноза, этот индекс представляет собой показатель влажности верхнего слоя почвы. Наиболее часто встречающимися показателями являются индекс предшествующего увлажнения и условия предшествующего увлажнения.

Методы, основанные на использовании показателя влажности почвы, обладают двумя важными особенностями при их применении в гидрологическом прогнозировании. Во-первых, поскольку этот показатель ежедневно обновляется, он подходит скорее для разового анализа отдельного гидрологического события, a не для непрерывного моделирования.

Следовательно, для того, чтобы применять его при составлении большинства прогнозов, необходимо разделить весь рассматриваемый период выпадения осадков на отдельные случаи или разделить каждый случай выпадения осадков на отдельные периоды. Например, во время длительного дождливого периода, прерываемого короткими периодами с малым количеством осадков или вовсе без осадков, может быть трудно решить, был ли это один ливень или несколько.

Вторая особенность применения индекса влажности почвы заключается в том, что при применении метода единичного гидрографа определяется только гидрограф поверхностного стока. Для построения гидрографа суммарного стока необходимо определять базисный сток каким-либо другим методом. Данный метод может применяться в оперативной практике только в тех случаях, когда имеет значение поверхностный сток, и единственно обоснованным является простой подход.