Основная теорема зацепления

Профили зубьев колес должны быть сопряженными, т. е. заданному профилю зуба одного колеса должен соответствовать вполне определенный профиль зуба другого колеса.
Чтобы выяснить, какова должна быть форма профиля зубьев пары колес, чтобы зацепление обеспечивало требуемое постоянство передаточного отношения, рассмотрим два зуба С иD, принадлежащих шестерне и колесу передачи и соприкасающихся в точке S (см. рисунок 2).

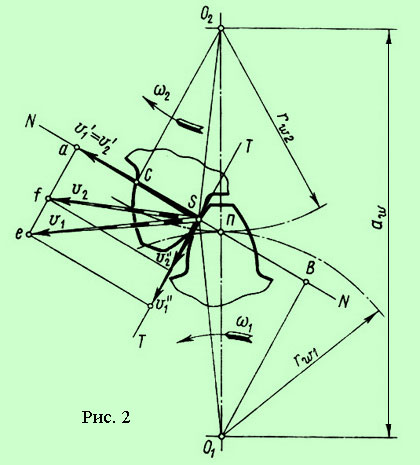
С – ведущее колесо с центром вращения О₁, а D– ведомое колесо с центром вращения в точке О₂. Расстояние a_w между центрами О₁ и О₂неизменно.
Зуб шестерни, вращаясь с угловой скоростью ω₁, оказывает давление на зуб колеса, сообщая ему угловую скорость ω₂.

Проведем через точку Sобщую для обоих профилей касательную ТТ и нормальNN.
Очевидно, что окружные скорости точки касания зубьев S относительно центров вращения О₁ и О₂будут равны:

v₁ = О₁Sω₁ и v₂ = О₂Sω₂.

v'₁/v₁ = О₁В/О₁S,

откуда получим:

v'₁ = v₁О₁В/О₁S = ω₁О₁В.

Из подобия треугольников afS и CSO₂ следует:

v'₂/v₂ = О₂С/О₂S,

откуда

v'₂ = v₂О₂С/О₂S = ω₂О₂С.

Но v'₁ = v'₂, следовательно:

ω₁О₁В = ω₂О₂С.

Передаточное число: u = ω₁/ω₂ = О₂С/О₁В. (1)

Нормаль NN пересекает линию центров О₁О₂ в точке П, называемой полюсом зацепления.
Из подобия треугольников О₂ПС и О₁ПВ следует:

О₂С/О₁В = О₂П/О₁П = r_w2/r_w1. (2)

Сравнивая соотношения (1) и (2), получим:

u = ω₁/ ω₂ = rw₂/ rw₁ = const. (3)

Это соотношение выражает основную теорему зацепления, которая может быть сформулирована следующим образом:
Для обеспечения постоянного передаточного числа зубчатых колес профили их зубьев должны быть очерчены по кривым, у которых общая нормаль NN, проведенная через точку касания профилей, делит расстояние между центрами О₁О₂ на части, обратно пропорциональные угловым скоростям.