Признаки подобия треугольников

Дано: DАВС, DА₁В₁С₁.

Первый признак. Второй признак. Третий признак.

ÐА=ÐА₁, ÐВ=ÐВ₁. ÐА=ÐА₁, . .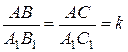

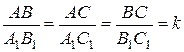Доказать: DАВС~ DА₁В₁С₁.

Доказательство.

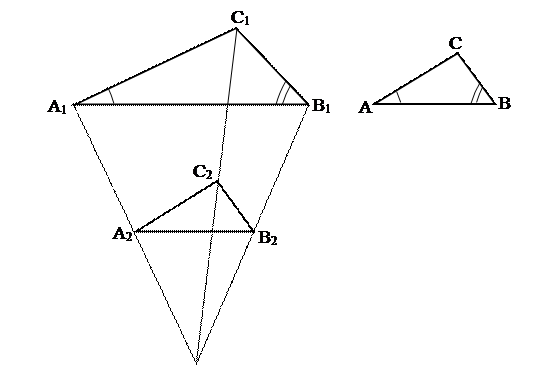
Рассмотрим гомотетию с произвольным центром и коэффициентом 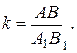Преобразуем посредством заданной гомотетии DА₁В₁С₁ в DА₂В₂С₂.

Докажем, что DАВС= А₂В₂С₂.

О

Первый признак.

ÐА=ÐА₁ (по условию), ÐА=ÐА₂ (по свойству гомотетии), следовательно,

ÐА₁=ÐА₂.

АВ = kА₁В₁ (по правилу задания гомотетии),

А₂В₂ = kА₁В₁ (по свойству гомотетии), следовательно, АВ = А₂В₂.

Треугольники АВС и А₂В₂С₂ равны по второму признаку.

Второй признак.

ÐА₁=ÐА₂,

АВ = А₂В₂

АС=kА₁С₁ (по условию), А₂С₂=kА₁С₁ (по свойству гомотетии), следовательно,

АС =А₂С₂.

Треугольники АВС и А₂В₂С₂ равны по первому признаку.

Третий признак.

АВ = А₂В₂ и АС =А₂С₂ (доказано выше).

Аналогично доказывается, что В₁С₁ = В₂С₂. Треугольники равны по третьему признаку.

Вывод: так как треугольники А₁В₁С₁ и А₂В₂С₂ гомотетичны (подобны), а треугольники А₂В₂С₂ и АВС равны (подобны), то посредством двух преобразований подобия треугольник АВС переводится в треугольник А₁В₁С₁ , следовательно, они подобны.