Локальное поле Лорентца

Локальным полем называют результирующую напряженность поля Е_л,действующего на молекулу в веществе. Это поле обусловлено наличием свободных зарядов на электродах, связанных зарядов и зарядов других молекул.

Величина локального поля определяет собой электрический момент молекулы и, следовательно, значение поляризации.

Наиболее просто локальное поле можно вычислить в случае нейтральных диэлектриков, в частности нейтральных газов. Индуцированный момент молекулы ,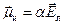

где α — поляризуемость молекулы и
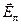— поле, действующее на молекулу (локальное).

Это поле отличается от среднего макроскопического поля. Поляризация равна сумме дипольных моментов молекул:

,

где сумма берется по всем молекулам единицы объема. Таким образом, для определения поляризации нужно вычислить величину локального поля, действующего на молекулы.

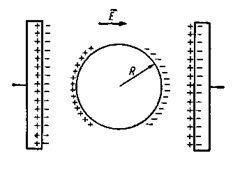Рис. 6‑5. К вычислению локального поля, действующего на молекулу в плоском конденсаторе

Рассмотрим плоский конденсатор с газообразным диэлектриком (Рис. 6‑5). В центральной части конденсатора вокруг какой-либо молекулы проведем сферу. Радиус R этой сферы выберем достаточно большим, порядка 100 диаметров молекулы или более, для того чтобы можно было считать диэлектрик за пределами сферы непрерывным и его свойства характеризовать диэлектрической проницаемостью ε и поле, действующее на молекулы в сфере, можно было выразить через величину поляризации Р. При вычислении электрического поля молекул, заключенных в сфере, нужно учитывать дискретное строение газа и вычислять поле от этих молекул как геометрическую сумму электрических полей, создаваемых каждым элементарным диполем.

Локальное поле E_л, действующее на молекулу, было вычислено Лорентцем. Оно может быть представлено в виде суммы трех слагаемых: среднего поля E_ср, создаваемого свободными зарядами на поверхности электродов и связанными зарядами в диэлектрике у поверхности электродов; поля E₁ создаваемого всеми молекулами за пределами сферы, за вычетом поля связанных зарядов, сосредоточенных у поверхности электродов, действие которых уже учтено в поле E_ср; поля E₂, создаваемого всеми молекулами внутри сферы, за исключением данной молекулы

.

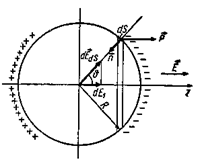Рис. 6‑6. К вычислению поля Elt создаваемого в сферической полости Лорентца связанными зарядами, которые находятся на ее поверхности

При вычислении поля Е₁ мы не учитываем поля, создаваемого всеми молекулами внутри сферы. Поле, создаваемое молекулами за пределами сферы, можно представить как поле от связанных зарядов на поверхности сферы и у поверхности электродов. Действие поля от связанных зарядов у поверхности электродов уже учтено при вычислении E_cp. Таким образом, Е₁ есть поле, создаваемое связанными зарядами на поверхности сферы (см. Рис. 6‑5). Вычислим напряженность этого поля, для чего направление поля выберем за направление оси z, которую проведем через центр сферы (Рис. 6‑6). Проведем под углом 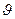к оси радиус, направленный в элемент поверхности dS; плотность связанного заряда на этом элементе поверхности

,

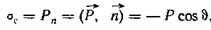где — вектор внешней нормали к поверхности диэлектрика, лежащего за пределами сферы (Рис. 6‑6).

Заряды на элементе поверхности dS создают поле , направленное под углом 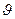к оси z. Проекция этого поля от зарядов на элементе поверхности dS на направление оси z обозначим через dE₁. Она равна

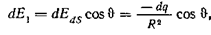
где dq —- заряд, находящийся на элементе dS;

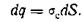
Подставив сюда величину σ_с из формулы , получим

Вычислим поле Е₁,создаваемое связанными зарядами на поверхности сферы. Заметим, что проекции поля Е₁ на оси x и y, перпендикулярные к оси z, равны нулю вследствие осевой симметрии. Таким образом, поле

,

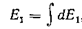где интегрирование производится по полям, создаваемым всеми зарядами на поверхности сферы.

Элемент поверхности в сферической системе координат

.

Из выражений , , и имеем

.

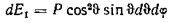Подставляя это значение dE₁ в , получаем

Таким образом, .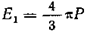

Для вычисления поля Е₂, действующего на молекулу в центре сферы со стороны всех других молекул в этой сфере, разобьем весь объем сферы на шаровые слои толщиной dr (Рис. 6‑7). Сначала вычислим поле, создаваемое всеми молекулами в шаровом слое с радиусом r, апотом произведем суммирование полей молекул, лежащих в различных шаровых слоях. Пусть в шаровом слое с радиусом r находится i-я молекула с индуцированным моментом μ_i. Поскольку мы считаем диэлектрик нейтральным, то направление всех индуцированных моментов совпадает с направлением среднего индуцированного момента и поля Е.

Этот индуцированный момент в центре сферы создает поле, напряженность которого 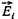определяется выражением

.

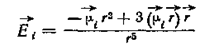Определим проекцию поля Е_i на ось z, для чего учтем, что направление 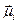, совпадает с направлением оси z. Таким образом,

,

где z_i — координата z для i-ймолекулы в декартовой системе координат, начало которой помещено в центре сферы.

Найдем составляющую поля вдоль оси z вцентре сферы от всех молекул, лежащих в шаровом слое радиусом r и толщиной dr, для чего возьмем сумму полей отдельных молекул, находящихся внутри слоя:

,

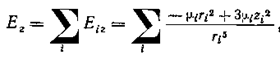где суммирование производится по всем молекулам, лежащим в шаровом слое;
r_i — радиус i-й молекулы,
r_i — r.

Поскольку радиус шарового слоя постоянен и индуцированные моменты всех молекул одинаковы, сумму можно переписать в виде

,

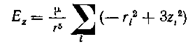Считая распределение молекул в сфере изотропным, имеем

.

Сопоставляя формулы и , видим, что Е_z= 0. Следовательно, поле, создаваемое в центре сферы всеми молекулами, лежащими внутри слоя, равно нулю. Проекции этого поля на оси х и у вследствие симметрии относительно оси z равны нулю, а проекция на ось z равна нулю, как показывают вычисления. Поскольку от каждого слоя поле равно нулю, то и суммарное поле всех слоев будет равно нулю. Таким образом, поле Е₂, действующее на молекулу в центре сферы со стороны всех других молекул, находящихся в сфере, равно нулю.

Поле Е₂ равно нулю в случае газов, неполярных жидкостей, которые мы считаем изотропными, и кубических кристаллов, для которых выполняется условие . Для неполярных кубических кристаллов это можно показать и непосредственно, если рассмотреть поле, действующее на какую-нибудь молекулу со стороны всех индуцированных диполей соседних молекул.

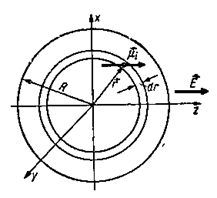Рис. 6‑7. К вычислению поля Е2, действующего на молекулу со стороны других молекул, расположенных внутри сферы Лорентца

Подставив значения Е₁, Е₂ и E_ср в формулу , найдем величину локального поля, действующего на молекулу в неполярных газах, жидкостях и кубических кристаллах,

.

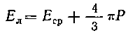Поле E_l, равное 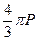, называется лорентцовым внутренним полем.

Выразим величину локального поля Е_лчерез напряженность среднего поля Е_ср. Для этого вспомним, что между поляризацией и средним полем существует соотношение . Подставив из него значение Р вформулу , найдем

.

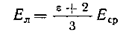В газах величина ε близка к единице, поэтому локальное поле по величине очень мало отличается от среднего поля. В неполярных жидкостях величина ε составляет две-три единицы, и локальное поле несколько больше среднего.