Макроскопическое поле в диэлектрике

Макроскопическое поле характеризуется средней напряженностью электрического поля в объеме, превышающем размеры молекулы, но достаточно малом, так что напряженность в пределах этого объема изменяется мало. В противоположность этому локальное поле — это поле, действующее на молекулу или другую способную поляризоваться частицу. В вакууме обе напряженности, макроскопическая и локальная, равны друг другу. В диэлектрической среде, кроме среднего макроскопического поля, на молекулу действуют поля соседних молекул. Таким образом, в диэлектрике (веществе) макроскопическое и локальное поля различны.

Поле в вакууме определяется распределением зарядов в про- странстве. Зная распределение зарядов, можно вычислить напряженность электрического поля, например, решая уравнение Пуассона

,

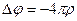где D — оператор Лапласа,
j— потенциал электростатического поля, ρ — плотность объемного заряда,

напряженность поля 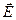находят из выражения

.

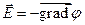Уравнение можно представить в виде

.

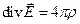Отсюда видно, что в областях, где нет объемных зарядов дивергенция напряженности электрического поля равна нулю .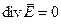

Потенциал j можно вычислить, пользуясь формулой

,

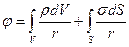где первый интеграл берется по всему пространству,
r — расстояние до элемента объема dV, в котором объемная плотность равна ρ, или до элемента поверхности dS, на котором поверхностная плотность равна σ;
второй интеграл берется по всем поверхностям, на которых имеются заряды с поверхностной плотностью σ.

Энергия W электростатического поля Е, создаваемого объемными зарядами с плотностью ρ и поверхностными зарядами с плотностью σ, определяется выражением

.

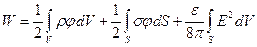Если имеется поверхность,на которой плотность заряда равна σ, то между нормальными составляющими электрического поля в областях 1 и 2 (Рис. 6‑1) и плотностью заряда σ соблюдается соотношение

,

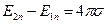где Е_2n — проекция напряженности поля 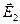в области 2 на направление нормали к поверхности ;
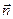Е_1n — проекция напряженности поля 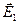в области 1 на направление нормали .

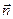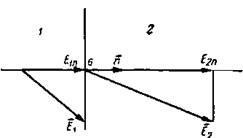Рис. 6‑1. Изменение напряженности электрического поля при переходе из области 1 в область 2 через заряженную плоскость с плотностью поверхностного заряда σ

Заряд, внесенный в диэлектрик (или избыточный заряд в диэлектрике), принято называть свободным зарядом q.

Электрическое поле Е заряда q в диэлектрике с диэлектрической проницаемостью ε в ε раз меньше, чем в вакууме:

.

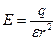Уменьшение поля от свободного заряда в диэлектрике по сравнению с полем от такого же свободного заряда в вакууме связано с поляризацией диэлектрика.

Если диэлектрик неполярный, его молекулы в электрическом поле приобретают индуцированные моменты, т. е. поляризуются, как показано на Рис. 6‑2; свободный заряд + q помещен в центре шарового диэлектрика, и молекулы изображены сильно увеличенными.

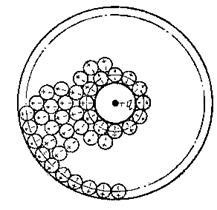Рис. 6‑2. Поляризация молекул неполярного диэлектрика в поле положительного заряда +q.

У свободных зарядов в сферической области, сечение которой на рисунке представлено внутренней тонкой, линией, имеется избыток связанных отрицательных зарядов — q_с. На внешней поверхности диэлектрика, за пределами сферы, изображенной на рисунке внешней (тонкой) окружностью, выделяется положительный связанный заряд +q_с, равный по абсолютной величине отрицательному заряду -q_с. В шаровом слое между двумя этими сферами положительные и отрицательные заряды компенсируются, т.е. суммарный заряд равен нулю.

Если заряженная частица q находится в дипольном диэлектрике, дипольные молекулы поворачиваются, так что вокруг этой частицы появляется отрицательный связанный заряд. Поэтому напряженность поля в диэлектрике

.

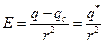С другой стороны, E можно выразить через величину свободного заряда q и диэлектрическую проницаемость ε. Из сравнения выражений и следует, что связанный заряд q_c. определяется значениями диэлектрической проницаемости ε и свободного заряда q:

.

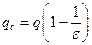Потенциал электрического поля в диэлектрике может быть определен из уравнений или . Однако под ρ и σ следует понимать суммарные плотности свободного и связанного зарядов. Эти уравнения для диэлектрической среды принимают вид:

,

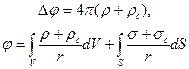где ρ и σ — объемная и поверхностная плотности свободного заряда;
ρ_с и σ_с — объемная и поверхностная плотности связанного заряда.

Электрическое поле в диэлектрике может быть определено через поляризацию диэлектрика 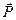. Пусть в плоском конденсаторе, левый электрод которого является анодом, а правый - катодом, находится нейтральный диэлектрик. Молекулы диэлектрика поляризуются, так что у анода появляется отрицательный, а у катода положительный связанный заряд (Рис. 6‑3, а).

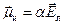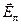Поскольку электрическое поле Е в плоском конденсаторе однородно, каждая молекула приобретает индуцированный момент , где — поле, действующее на молекулу (локальное), которое может быть больше Е.

Если в единице объема находится п молекул, то момент единицы объема

.

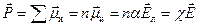Величина 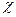, равная nα, называется диэлектрической восприимчивостью диэлектрика. В случае неоднородного поля под поляризацией вещества 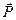понимают отношение электрического момента 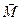некоторого малого объема диэлектрика к величине этого объема :

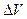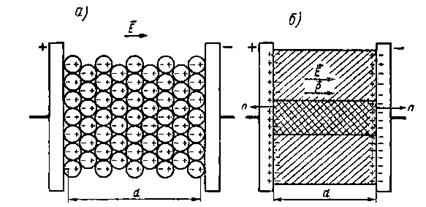Рис. 6‑3. Поляризация диэлектрика в плоском конденсаторе: а — возникновение индуцированных моментов молекул под действием электрического поля; б — образование связанных зарядов на поверхности у электродов

.

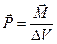Выражения и справедливы в случае всех механизмов поляризации, кроме спонтанной поляризации в сегнетоэлектриках.

Выделим в плоском конденсаторе столбик единичного сечения; на Рис. 6‑3, б он отмечен более густой штриховкой. Заряд на электродах такого элемента равен поверхностной плотности σ.

Плотность зарядов на электродах вакуумного конденсатора σ_в в ε раз меньше плотности зарядов σ на электродах конденсатора с диэлектриком

,

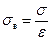а напряженности при одинаковых напряжениях одинаковы для обоих конденсаторов.

Напряженность поля связана с плотностью зарядов на обкладках вакуумного конденсатора соотношением

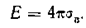
Поле в конденсаторе с диэлектриком создается свободным зарядом на электродах с плотностью σ и связанным зарядом на поверхности диэлектрика с плотностью σ_с. Свободный и связанный заряды в плоском конденсаторе создают поля, направленные навстречу друг другу. Результирующее поле

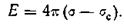
Так как напряженность поля в том и другом конденсаторе одинакова, приравняв правые части формул и , получим согласно

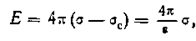
отсюда

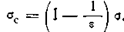
Сравнивая формулы и , видим, что оба соотношения между величинами свободного и связанного зарядов подобны друг другу.

Принимая во внимание, что в плоском конденсаторе 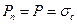, из находим

,

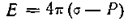откуда

.

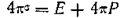Как видно из , при заданном свободном заряде на электродах σ поле в конденсаторе зависит от ε. В плоском конденсаторе электрическая индукция (электрическое смещение) определяется величиной свободного заряда:

.

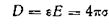В случае изотропных диэлектриков справедливо векторное равенство

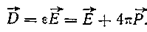
Подставляя в это равенство величину 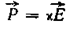получаем

.

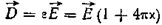Отсюда находим соотношение между диэлектрической проницаемостью ε и диэлектрической восприимчивостью х

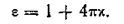
Из следует, что

.

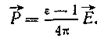Если в диэлектрике или на границе раздела диэлектриков имеется заряженная поверхность с поверхностной плотностью свободных зарядов σ, то вместо соотношения получаем

,

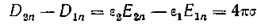где ε₁ и ε₂ — значения диэлектрической проницаемости в областях 1 и 2 и D_2n и D_1n — проекции вектора электрической индукции в областях 1 и 2 на направление внешней нормали к поверхности, ограничивающей область 1 (см. Рис. 6‑1).

В частности, если на поверхностях раздела диэлектриков 1 и 2 нет свободных зарядов, то

.

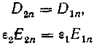Следовательно, при отсутствии свободных зарядов на поверхности раздела двух различных диэлектриков ( 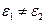) нормальная составляющая электрической индукции на этой поверхности остается непрерывной, а нормальная составляющая напряженности испытывает скачок.

На грани двух различных диэлектриков 1 и 2 тангенциальные составляющие напряженности электрического поля остаются непрерывными, а тангенциальные составляющие электрической индукции испытывают скачок

,

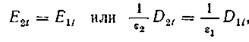где E_1t и D_lt — тангенциальные составляющие напряженности электрического поля и электрической индукции на поверхности раздела в первом диэлектрике;
E_2t и D_2t — тангенциальные составляющие напряженности электрического поля и электрической индукции на поверхности раздела во втором диэлектрике.

Из выражений и вытекает, что на поверхности раздела двух сред с диэлектрической проницаемостью ε₁ и ε₂ силовые линии электрического поля Е и параллельные им линии электрической индукции испытывают преломление:

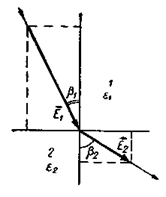Рис. 6‑4. Преломление силовых линий электрического поля при переходе через поверхность раздела двух диэлектриков с различными диэлектрическими проницаемостями

,

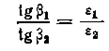где β₁ и β₂ — углы, образующиеся между нормалью к поверхностям раздела и направлением силовых линий в средах 1 и 2 (Рис. 6‑4).

Линии электрического поля Е могут оканчиваться на поверхностях раздела диэлектриков. Линии электрической индукции D непрерывны на поверхностях раздела диэлектриков, если на этих поверхностях нет свободных зарядов. Линии электрической индукции начинаются на положительном и оканчиваются на отрицательном свободном заряде. В частности, если имеется проводник, на поверхности которого находится заряд с плотностью σ, то

,

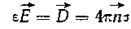где 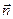— внешняя нормаль к поверхности проводника;
ε — диэлектрическая проницаемость диэлектрика, окружающего проводник.

Энергия электрического поля диэлектрика определяется выражением

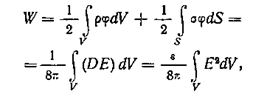
где ρ и σ — объемная и поверхностная плотности свободного заряда;
j — потенциал электрического поля в диэлектрике.

Это выражение подобно формуле , определяющей энергию электрона в вакууме через плотность свободного заряда. Влияние диэлектрика сказывается в том, что при одинаковом распределении свободных зарядов потенциал в диэлектрике j отличается от потенциала в вакууме.