ИНТЕГРИРУЮЩАЯ ЦЕПЬ RC

ИНТЕГРИРУЮЩИЕ И ДИФФЕРЕНЦИРУЮЩИЕ RC-ЦЕПИ

В радиоэлектронике и электротехнике интегрирующие и дифференцирующие цепи широко применяются в импульсной технике для преобразования одной формы импульсов в другую. В частности:

1) Интегрирующие цепи используются:

- для получения сигналов, пропорциональных интегралу от входных сигналов (с определенной погрешностью);

- для фильтрации высокочастотных составляющих;

- для удлинения фонтов импульсов;

- для увеличения длительности импульсов;

- для формирования линейно-изменяющихся напряжений.

2) Дифференцирующие цепи используются:

- для получения сигналов, пропорциональных производной от входных сигналов (с определенной погрешностью);

- для устранения постоянной составляющей сигнала;

- для уменьшения длительности импульса;

- для получения двухполярных импульсов из однополярных.

ИНТЕГРИРУЮЩАЯ ЦЕПЬ RC

Найдем выходное напряжение U_out, снимаемое с клемм, подключенных к конденсатору. Для этого рассмотрим электрическую цепь из резистора сопротивлением R и конденсатора ёмкостью C, представленную на рисунке Рисунок 1.

Рисунок 1 – Интегрирующая RC-цепь

Элементы R и C соединены последовательно, значит, ток в их цепи можно выразить, исходя из производной напряжения заряда конденсатора

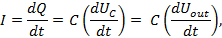
где Q – заряд конденсатора, C – емкость конденсатора, U_C – напряжение между обкладками конденсатора и закона Ома

где I – ток, протекающий в RC-цепи, U_R – напряжение на резисторе, R – сопротивление резистора.

Тогда будет иметь место равенство:

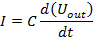
или

Проинтегрируем последнее выражение:

Интеграл левой части уравнения будет равен U_out + Const. Перенесём постоянную составляющую Const в правую часть с тем же знаком. В правой части постоянную времени RC вынесем за знак интеграла:

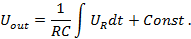
В итоге получилось, что выходное напряжение U_out прямо-пропорционально интегралу напряжения на выводах резистора, следовательно, и входному току I_in.
Постоянная составляющая Const не зависит от номиналов элементов цепи.

Чтобы обеспечить прямую пропорциональную зависимость выходного напряжения U_out от интеграла входного U_in, необходима пропорциональность входного напряжения U_in от входного тока I_in.

Нелинейное соотношение 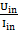во входной цепи вызвано тем, что заряд и разряд конденсатора происходит по экспоненте 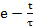, которая наиболее нелинейна при 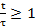, то есть, когда значение t соизмеримо или больше τ. Здесь t - время заряда или разряда конденсатора в пределах периода,
τ = RC - постоянная времени. Если взять номиналы RC цепи, когда τ будет значительно больше t, тогда начальный участок экспоненты для короткого периода (относительно τ) может быть достаточно линейным, что обеспечит необходимую пропорциональность между входным напряжением и током.

Для простой цепи RC постоянную времени обычно берут на 1-2 порядка больше периода переменного входного сигнала, тогда основная и значительная часть входного напряжения будет падать на выводах резистора, обеспечивая в достаточной степени линейную зависимость:

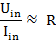
В таком случае выходное напряжение U_out будет с допустимой погрешностью пропорционально интегралу входного напряжения U_in. Чем больше величины номиналов RC, тем меньше переменная составляющая на выходе, тем более точной будет кривая функции.

Пример №1. В качестве примера, сигнал с генератора в виде положительного меандра с уровнем напряжения 1В, периодом 2 мс подадим на вход простой интегрирующей RC-цепи со следующими параметрами: R = 10 кОм, С = 1 мкФ. Тогда постоянная времени τ = RC = 10 мс. В данном случае постоянная времени лишь в пять раз больше времени периода, но визуально интегрирование прослеживается в достаточной степени точно.

График на рисунке Рисунок 2 показывает, что выходное напряжение на уровне постоянной составляющей 0,5В будет треугольной формы, потому как участки, не меняющиеся во времени, для интеграла будут константой (обозначим её a), а интеграл константы будет линейной функцией:

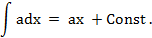
Величина константы a определит тангенс угла наклона линейной функции.

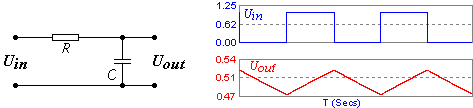
Рисунок 2 - Вид меандра после прохождения интегрирующей RC-цепи

Пример №2. На вход интегрирующей RC-цепи подадим сигнал в виде синусоиды. Проинтегрируем синусоиду, получим косинус с обратным знаком (см. рисунок Рисунок 3):

В данном случае постоянная составляющая Const = 0.

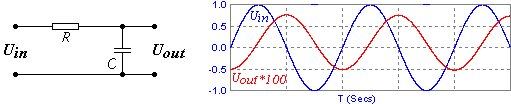
Рисунок 3 – Вид синусоиды после прохождения интегрирующей RC-цепи

Недостаток простейшей интегрирующей RC-цепи в том, что переменная составляющая на выходе получается очень маленькой относительно входного напряжения.