Представление о задаче

Способность решить задачу зависит не только от стратегии ее декомпозиции, но также и от того, как мы ее себе представляем. Иногда лучшим оказывается представление в форме высказываний (пропозициональная репрезентация); в других случаях более эффективным будет зрительное представление, или образ, Для иллюстрации рассмотрим следующую задачу:

«Однажды утром, на рассвете, монах стал взбираться на гору. Узкий проход шириной один или два фута спиралью обвивал гору, ведя к храму на вершине. Монах взбирался с разной скоростью, часто прерывая путь для отдыха. Он добрался до храма незадолго перед закатом. Проведя несколько дней в храме, он начал свой путь назад по тому же пути, выйдя на рассвете, и снова шел с разной скоростью со многими остановками в пути. Его средняя скорость спуска была, конечно, больше средней скорости взбирания на гору. Докажите, что на пути существует определенное место, в котором монах находился в обоих походах точно в одно и то же время дня» (Adams, 1974, р. 4).

Пытаясь решить эту задачу, многие люди начинают с пропозициональной репрезентации. Они могут даже пытаться выписать ряд уравнений и вскоре запутываются. Эту задачу гораздо легче решить, если представлять ее зрительно. Все, что надо сделать, — это представить мысленно, как путь монаха вверх накладывается на его путь вниз. Вообразите одного монаха, идущего снизу, а другого — идущего сверху. Независимо от того, какая у них скорость, в некоторый момент времени и в некотором месте пути они должны встретиться. Поэтому должно существовать место на пути, которое монах занимал в обоих путешествиях в то же самое время дня (заметьте, что в задаче не спрашивается, где находится это место).

<Рис. Наглядные учебные пособия помогают учащимся визуализировать математические задачи.>

Некоторые задачи легко решаются путем манипулирования высказываниями либо образами. Это можно показать на следующей простой задаче: «Эд бегает быстрее Дэвида, но медленнее Дэна; кто из троих самый медленный?». Чтобы решить эту задачу при помощи высказываний, заметим, что первую часть этой задачи можно представить в виде высказывания, в котором «Дэвид» — это субъект, а «медленнее, чем Эд» — предикат. Вторую часть задачи можно представить в виде высказывания, в котором «Эд» — субъект, а «медленнее Дэна» — предикат. Затем можно вывести, что Дэвид медленнее Дэна, откуда следует, что самый медленный — Дэвид. Чтобы решить эту задачу через образы, можно, например, вообразить скорости этих трех человек в виде трех точек на линии, вот так:

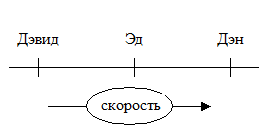
Затем можно просто считать ответ на вопрос непосредственно из образа. Очевидно, что некоторые люди предпочитают представлять такие задачи в виде высказываний, а некоторые — зрительно (Johnson-Laird, 1985).

Помимо представления задачи на языке высказываний либо образов существует вопрос о том, что представлять. Зачастую трудности с задачами возникают потому, что нам не удается включить в свою репрезентацию задачи какой-либо решающий фактор, или потому, что мы включили в нее что-то, что не является существенной частью задачи. Это можно проиллюстрировать в эксперименте. Одной группе испытуемых дали задачу закрепить свечку на двери, дав только материалы, показанные на рис. 9.13.

Рис. 9.13. Материалы для решения задачи со свечой.Как, имея изображенные здесь материалы (упаковка со свечками, спички в большом спичечном коробоке, канцелярские кнопки, тонкая веревка), закрепить свечку на двери? Решение показано на следующей странице (Glucksberg & Weisberg, 1966).

Решение заключалось в том, чтобы прикрепить дно выдвижной части коробка к двери кнопками и использовать торец этой части как подставку для свечки. Большинству испытуемых было трудно ее решить, видимо, потому, что они представляли себе коробку как емкость, а не как подставку. Другой группе испытуемых задали ту же задачу, но вынули содержимое из коробки. Эти испытуемые успешнее решали задачу, видимо потому, что они с меньшей вероятностью включали в свою репрезентацию функцию коробки как емкости и с большей вероятностью учитывали ее функцию как подставки.

Решение задачи со свечой.

Исследования, подобные этому и другим, рассмотренным в данном разделе, позволяют понять, почему многие эксперты считают, что хорошая репрезентация задачи — это половина успеха на пути к ее решению. (Этапы решения этой задачи представлены в табл. 9.2.)

Таблица 9.2. Этапы решения задачи

1. Представить проблему как высказывание или в визуальной форме.

2. Определить цель.

3. Разбить цель на подцели.

4. Выбрать стратегию решения задачи и использовать ее для решения каждой из подцелей.

Эксперты и новички

В той или иной предметной области (например, физике, географии или шахматах) эксперты решают задачи качественно иным способом, чем новички. Это объясняется различиями в используемых ими репрезентациях и стратегиях. В памяти экспертов может храниться больше конкретных репрезентаций, которые они могут использовать для решения задачи. Мастер по шахматам, например, может посмотреть 5 секунд на сложную комбинацию на доске, включающую 20 фигур, и в точности ее воспроизвести; новичок в той же ситуации ограничен обычными 7 ± 2 элементами (см. гл. 8). Такой трюк с памятью удается экспертам потому, что с годами практики они разработали репрезентации многих возможных позиций на доске; эти репрезентации позволяют им закодировать сложную позицию всего в нескольких единицах. Кроме того, предположительно именно эти репрезентации лежат в основе их превосходства в шахматной игре. Мастер может хранить целых 50 000 конфигураций и знать, что делать в каждой из них. Итак, мастера шахмат могут, по сути, «видеть» возможные ходы; им не надо их выдумывать, как поступают новички (Chase & Simon, 1973; Simon & Gilmartin, 1973).

Даже встречаясь с новой задачей, эксперт представляет ее иначе, чем новичок. Этот момент хорошо проиллюстрирован в исследованиях решения задач в физике. Эксперт (скажем, профессор физики) представляет задачу на языке физических принципов, нужных для ее решения, например: «эта задача относится к типу: всякое действие вызывает равное и противоположно направленное противодействие». Новичок (скажем, студент-физик первого курса), напротив, представляет ту же самую проблему на языке поверхностных свойств, например: «это задача из рода задач с наклонной плоскостью» (Chi, Glaser & Rees, 1982).

Эксперты и новички различаются также используемыми стратегиями. В исследованиях решения физических задач эксперты в общем стараются сформулировать план подхода к задаче, прежде чем выводить уравнения, тогда как новички, как правило, начинают писать уравнения, не имея в голове общего плана (Larkin et al., 1980). Еще одно различие состоит в том, что новички работают в противоположном направлении (стратегия движения от цели). Это различие в направлении рассуждения также было выявлено в исследованиях решения задач врачами. Большинство экспертов-врачей рассуждают в прямом направлении — от симптома к возможному заболеванию, тогда как менее опытные их коллеги рассуждают в обратном направлении — от возможного заболевания к симптому (Patel & Groen, 1986).

<Рис. Эксперты решают шахматную задачу качественно иначе, чем новички. Такие эксперты, как мастера игры в шахматы, хранят в своей памяти намного больше специфических репрезентаций, чем они могут применить для решения проблемы.>

Рассмотренные характеристики компетентности — множественность репрезентаций; репрезентации, основанные на определенных правилах; планирование перед действием; движение вперед — это некоторые из предметно-ориентированных процедур, которые приходят на смену слабым методам решения задач, рассмотренным ранее.