Не рассматриваются переходные процессы установления движения Крови.

Существует “внешний механизм” закрытия и открытия аортального клапана, определяемый активной деятельностью сердца.

При поступлении крови из сердца часть ее размещается в крупных сосудах, растягивая их, а часть избытка крови протекает в мелкие сосуды. Можно записать уравнение баланса объема крови;

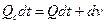(9)

где Q_c(t) - объемная скорость поступления крови из сердца (рис. 6б), Q(t) - объемная скорость кровотока в начале мелких сосудёв, dv — изменение объема крупных сосудов.

Предполагаем, что изменение объема резервуара линейно зависит от изменения давления в нем dP

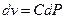(10)

где С — эластичность - коэффициент пропорциональности между давлением и объемом, .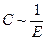

Условно считая давление Р₀ на выходе из жесткой трубки равным 0 и применяя для течения крови по ней закон Пуазейля, получим, что

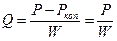(11)

где Р(t) давление в крупных сосудах (в том числе на входе в мелкие), W - гидравлическое сопротивление мелких сосудов.

Систему уравнений (9, 10, 11) можно решить относительно Р(t) , Q(t) или v(t). Решим систему относительно Р(t).

Фаза

С учетом 9, 10, 11 получим уравнение

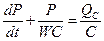(12)

Это неоднородное линейное дифференциальное уравнение, решение которого определяется видом функции Q_c(t).

Будем считать Q_c равной ее среднему значению Q₀ за время между открытием и закрытием аортального клапана. Тогда уравнение (12) запишется:

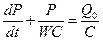
Считая, что при t=0 давление Р = Р_д, получим:

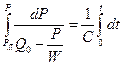
В результате находим закон повышения Р(t) в крупных сосудах с момента открытия и до закрытия аортального клапана:

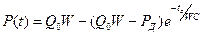(13)

Считаем, что через время t_c срабатывает механизм закрытия аортального клапана, при этом давление крови в крупных сосудах достигнет некоторого значения Р_с:

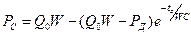(14)

В зависимости (14) аргументом является не текущее время как в(13), а время систолы t_c.

Примечание. Зависимость (13) получена в предположени постоянной скорости поступления крови из сердца в течение t_c.

Q_c=Q₀ . Для расширения границ применимости модели необходимо учитывать не только собственные параметры W и С определяющие релаксационные процессы в системе сосуд–кровь, но и конкретный вид временной зависимости внешнего воздействия на систему, а именно Q_c(t). Учет зависимости скорости поступления крови из сердца в аорту, представленной на рис. 6б, приведет к несколько другому закону нарасталня давления крови в моменты времени 1à2, когда Q_c(t) возрастает до максимального значения, а также позволит найти зависимость падения давления крови в аорте в моменты времени 2à3, когда Q_c падает до нуля.

Фаза

Вторая фаза начинается с момента закрытия аортального клапана (т.3 на рис. 6б). Именно этот момент будем считать начальным для 2 фазы. Модель Франка позволяет аналитически найти зависимость падения давления Р(t) в крупном сосуде после закрытия аортального клапана.

Поскольку кровь уже не поступает из сердца, то Q_c=0 . Тогда уравнение (9) превращается в:

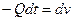(15)

Знак минус отражает уменьшение объема крупного сосуда с течением времени.

С учетом (10),

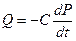
С учетом (11) получаем дифференциальное уравнение:

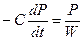(16)

Начальное условие : при t=0 (соответствует закрытию клапана) считаем давление Р=Р_с. (В данной модели не учитываем различие давлений в т. 2 и 3, считая давление в т. 3 равным систолическому). В результате получаем закон изменения давления в крупных сосудах с момента закрытия аортального клапана:

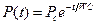(17)

На рис. 7 приведена зависимость спада давления в крупных сосудах после закрытия аортального клапана.

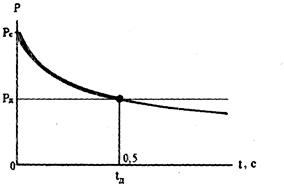
Рис 7 Зависимость давления крови от времени в крупном сосуде после закрытия аортального клапана

Через некоторое время (t_д) давление упадет до диастолического

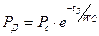
После чего открывается клапан, тем самым закичивается фаза 2 и начинается опять фаза 1.

зависимость (17) качественно описывает экспериментальную зависимость Р(t) в аорте, приведенную на рис. 6а в т. 3à1^’.