Математическая модель оптимизации состава агрегатов
Рассмотрим определенный состав агрегатов и оценим изменение расхода топлива в системе, которое дает останов или пуск одного из агрегатов. Задача решается для тепловой системы, и оптимизируется состав работающих блоков тепловых станций (в принципе могут рассчитываться и ТЭС с поперечными связями).
Общая модель задачи.
1. Уравнение цели, которое определяет экономию от останова j -го агрегата, следующее:
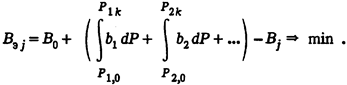 (8)
(8)
За счет отключения j-го агрегата с расходом Вj - изменится режим системы. Это приведет к новому распределению мощностей между работающими агрегатами. Тогда оставшийся в работе первый агрегат будет иметь мощность Р1k вместо Р1,0 , второй агрегат будет иметь мощность Р2k вместо Р2,0 и т. д.
Если относительные приросты соответствуют их среднему значению, то (8) можно записать так:
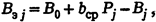
где Pj - нагрузка j-го агрегата; B0 - первоначальный (до изменения состава) расход топлива.
2. Уравнение связи - это расходные характеристики агрегатов Bi(Pi), где i - номер агрегата и i = 1, 2, ..., j ...
3. Уравнения ограничений включают балансовые уравнения мощности
 , (10)
, (10)
где k - номера агрегатов, остающихся в работе: k Î i. Кроме того, учитываются ограничения по допустимым мощностям агрегатов:
Pk min £ Pk £ Pk max (11)
4. Уравнение оптимизации составляется для отыскания оптимальной стратегии управления составом агрегатов. В оптимальной стратегии указывается рациональный порядок (очередность) отключения либо подключения агрегатов. Используются условия (5)-(7) в зависимости от конкретных условий.
Выбор стратегии останова агрегатов для заданного графика нагрузки с учетом пусковых расходов. При выполнении расчетов по заданному графику нагрузки системы может оказаться, что агрегат отключается на определенную часть расчетного периода, а затем требуется включение этого же или нового агрегата. В этом случае необходимо учитывать пусковые расходы. Если пусковые расходы Впуск зависят от времени простоя агрегата, то отключать блок выгодно только в том случае, когда экономия от останова агрегата на время простоя будет больше чем расход топлива на последующий пуск, т.е. выполняется условие
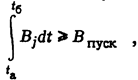 (12)
(12)
где tа и tб - моменты останова и пуска блока.
В том случае, когда пусковые расходы линейно зависят от простоя агрегата, отключение агрегата выгодно при
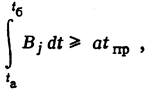 (13)
(13)
где tпр - время простоя агрегата; а - постоянный множитель.
Пусковые расходы можно учесть в критерии выгодности отключения, внеся в него соответствующую поправку, а именно
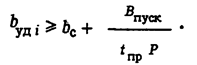 (14)
(14)
Второе слагаемое в правой части неравенства (14) позволяет учесть дополнительный расход топлива на покрытие нагрузки системы P, который появляется за счет пусковых расходов. Эти величины совпадают по размерности.
Учет пусковых расходов сдвигает условия выгодности останова в зону меньших нагрузок агрегата по сравнению с экономическими мощностями и нарушает однозначную пускоостановочную стратегию управления агрегатами. Для того чтобы решить задачу, требуется итерационный расчет. Вначале находят режим агрегатов без учета пусковых расходов для всех интервалов времени. По полученным данным находят время простоя агрегата и по (14) уточняют момент отключения.
Алгоритм расчета. Расчет осуществляется итеративно. Вначале для постоянных интервальных нагрузок Pt (график нагрузок на период t задается осредненными нагрузками Pt на интервалах t) находятся состав и мощности агрегатов без учета пусковых расходов. Для этого выбирается произвольно значение относительного прироста и по критерию, например (5), отбираются работающие т агрегатов и определяется суммарная мощность выбранных агрегатов при наивыгоднейшем распределении нагрузки между ними. Если имеется равенство между заданной нагрузкой и мощностями агрегатов, то состав определен. В случае неравенства увеличивается либо уменьшается относительный прирост системы. Далее расчеты повторяются до получения баланса между нагрузкой и мощностями агрегатов.
На основании таких расчета определяется временная диаграмма работы и простоя каждого агрегата. Используя ее, можно уточнить расчеты с учетом пусковых расходов.
Определяются пусковые расходы для всех m агрегатов для каждого интервала простоя. С использованием (14) намечается новый состав работающих агрегатов и заново уточняются пусковые расходы. Путем итеративных расчетов находится окончательный состав работающих агрегатов.
Вопрос: Как влияние оказывают на критерий выгодности отключения увеличение 1) пусковых расходов на запуск агрегата; 2) времени простоя агрегата?
Дата добавления: 2016-06-15; просмотров: 1954;











