Основные аксиомы алгебры логики

Из теоремы о функциональной полноте следует, что с помощью некоторых совокупностей логических функций, удовлетворяющих условиям теоремы, можно строить произвольные логические функции, зависящие от конечного числа переменных. Для решения этой задачи необходимо сформировать систему аксиом и правил преобразования, т.е. разработать алгебру, в основу которой должна быть положена выбранная функционально полная система функций.

Исторически первой была разработана алгебра логики, которая включает три элементарные логические функции (операции): конъюнкцию, дизъюнкцию и инверсию. Начало исследований этой алгебры положено в трудах английского ученого Дж. Буля. В связи с этим эту алгебру нередко называют булевой алгеброй или алгеброй Буля.

Алгеброй логики называется совокупность элементов 0,1, х₁, х₂, ..., х_n и операций дизъюнкции, конъюнкции и инверсии, для которых выполняются перечисленные ниже аксиомы.

1. Операции дизъюнкции и конъюнкции:

- ассоциативны (сочетательны):

x₁Ú(x₂Úx₃ )=(x₁Úx₂)Úx₃;

x₁(x₂x₃)=(x₁x₂)x₃;

- коммутативны (переместительны):

x₁Úx₂=x₂Úx₁;

x₁x₂=x₂x₁;

- дистрибутивны (распределительны):

x₁Úx₂x₃=(x₁Úx₂)Ú(x₁Úx₃);

x₁(x₂Úx₃)=x₁x₂Úx₁x₃.

2. Для каждого х существует х (инверсия или отрицание х) такой, что

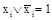
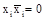
3. Элементы 0 и1 такие, что

xÚ0=x;

xÚ1=1;

x×0=0;

x×1=x;

`0=1;

`1=0.

4. Для всех элементов х_i(i=1,2, ..., n):

x_iÚx_i ...Úx_i =x_i;

x_i×x_i...x_i=x_i;

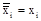
5. Для любых элементов:

;

.

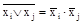Эти аксиомы называются правилами инверсии.

Рассмотренные аксиомы применимы не только к определенным переменным, но и к группам переменных, объединенных введенными операциями. На базе этих аксиом может быть получено множество тождественных соотношений, которые широко используются в практике преобразования логических формул. Приведем некоторые из них:

x₁Úx₁x₂=x₁; x₁(x₁Úx₂)=x₁;

.

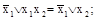
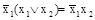В более общем виде:

x_iÚ f (x₁, x₂, ..., x_i, ..., x_n)= x_iÚ f (x₁, x₂, ..., 0, ..., x_n);

`x<sub>i</sub>Ú f (x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>i</sub>, ..., x<sub>n</sub>) = `x_iÚ f (x₁, x₂, ..., 1, ..., x_n);

x_i f (x₁, x₂, ..., x_i, ..., x_n)= x_i f (x₁, x₂, ..., 1, ..., x_n);

`x<sub>i</sub> f (x<sub>1</sub>, x<sub>2</sub>, ..., x<sub>i</sub>, ..., x<sub>n</sub>) = `x_i f (x₁, x₂, ..., 0, ..., x_n).

Рассмотрим порядок выполнения действий в алгебре логики. При отсутствии в выражении скобок первыми должны выполняться операции отрицания, затем операции конъюнкции и последними операции дизъюнкции. Наличие в выражении скобок изменяет обычный порядок действий. При этом в первую очередь производятся операции внутри скобок.