Определение тупиковых форм логических функций с помощью импликантных (имплицентных) таблиц
Располагая полной системой простых импликант (имплицент) логической функции, можно определить все ее тупиковые формы. Сравнение тупиковых форм логической функции позволяет найти ее минимальную (минимальные) форму.
Для определения всех приведенных систем простых импликант широко используются импликантные (имплицентные) таблицы.
Импликантная (имплицентная) таблица представляет собой двухвходовую таблицу, строки которой обозначаются простыми импликантами (имплицентами) логической функции, а столбцы - единичными (нулевыми) наборами минимизируемой логической функции  . Если простая импликанта (имплицента) покрывает единичный (нулевой) набор функции, то клетка, находящаяся на пересечении соответствующих им строки и столбца, отмечается условным знаком, например, звездочкой. Заполнять таблицу удобно, если ее строки обозначать вместо простых импликант (имплицент) соответствующими им группами соседних наборов. Очевидно, что простая импликанта (имплицента) накрывает тольео те рабочие (запрещенные) наборы функции, которые вошли в соответствующую ей группу соседних наборов.
. Если простая импликанта (имплицента) покрывает единичный (нулевой) набор функции, то клетка, находящаяся на пересечении соответствующих им строки и столбца, отмечается условным знаком, например, звездочкой. Заполнять таблицу удобно, если ее строки обозначать вместо простых импликант (имплицент) соответствующими им группами соседних наборов. Очевидно, что простая импликанта (имплицента) накрывает тольео те рабочие (запрещенные) наборы функции, которые вошли в соответствующую ей группу соседних наборов.
Для удобства работы с таблицей каждая импликанта (имплицента) функции обозначается буквой латинского алфавита. На основании импликантной (имплицентной) таблицы легко определить все приведенные системы простых импликант (имплицент). При анализе таблицы прежде всего выделяются столбцы, содержащие только одну отмеченную клетку. Импликанты (имплиценты) , соответствующие таким клеткам, должны обязательно входить во все приведенные системы простых импликант (имплицент) логической функции, так как только они покрывают наборы, соответствующие столбцам, в которых расположены эти единственные отмеченные клетки. Такие импликанты (имплиценты) образуют ядро логической функции.
Чтобы определить приведенные системы простых импликант (имплицент), необходимо найти минимальные их совокупности, которые покрывали бы все единичные (нулевые) наборы, не покрытые импликантами (имплицентами) ядра функции.
Пример 3.8.Определим тупиковую ДНФ логической функции, для которой задана импликантная таблица 3.1.
Таблица 3.1
Импликантная таблица к примеру 3.8
| Простые | Единичные наборы | ||||
| импликанты | |||||
| A`x1`x2`x3 x4`x5`x6 | * | ||||
| B`x1 x2`x3`x4`x6 | * | ||||
| C x1 x2 x4 x6 | * | * | |||
| D`x1 x4 x5 x6 | * | ||||
| E x1 x2 x3 | * | * | |||
| F x2 x5 | * | * | * |
В рассматриваемом примере только один единичный набор 10 покрывается одной импликантой А. Следовательно, импликанта А образует ядро логической функции. Оставшиеся единичные наборы 57, 62, 76, 77 покрываются парами импликант С, F или Е, F. Перечисленные пары простых импликант образуют минимальные совокупности, покрывающие указанные единичные наборы, так как исключение любой импликанты приводит к тому, что часть наборов окажется непокрытой. Таким образом, в результате анализа таблицы 3.1 определены две приведенные системы простых импликант логической функции :
A, C, F и A, E, F.
Объединяя простые импликанты приведенной системы знаком дизъюнкции, получим две тупиковые ДНФ логической функции:
 ;
;
 .
.
Описанный метод непосредственного исследования импликантной (имлицентной) таблицы применим только для относительно простых таблиц.
Для определения всех приведенных систем простых импликант (имплицент) логических функций используется алгебраический метод исследования импликантных (имплицентных) таблиц . Суть метода состоит в том, что непосредственно по таблице составляется логическое выражение Ф, которое отражает характер покрытия наборов импликантами (имплицентами). Преобразование этого выражения позволяет определить все минимальные покрытия.
Алгоритм решения задачи определения всех тупиковых форм логической функции по импликантной (имплицентной) таблице состоит в следующем.
1. Для каждого столбца импликантной (имплицентной) таблицы составляется дизъюнкция импликант (имплицент), которые покрывают единичный (нулевой) набор, соответствующий данному столбцу. Знак дизъюнкции соответствует тому, что в приведенную систему импликант (имплицент) должна обязательно входить хотя бы одна импликанта (имплицента), покрывающая рассматриваемый набор.
2. Дизъюнкции простых импликант (имплицент), записанные для каждого столбца таблицы, объединяются знаком конъюнкции. Это соответствует тому, что каждая приведенная система простых импликант должна покрывать все единичные (нулевые) наборы функции.
3. Полученное таким образом выражение Ф преобразуется в соответствии с аксиомами и тождествами алгебры логики к дизъюнктивной нормальной форме.
4. Каждая конъюнкция полученного выражения содержит в виде сомножителей совокупность простых импликант (имплицент), составляющих приведенную систему, а число конъюнктивных членов выражения равно числу всех приведенных систем простых импликант (имплицент), т.е. числу тупиковых форм логической функции. Поэтому для определения тупиковой ДНФ (КНФ) необходимо простые импликанты (имплиценты), вошедшие в одну конъюнкцию выражения Ф, объединить знаком дизъюнкции (конъюнкции).
Пример 3.9.Определим все тупиковые и минимальные ДНФ логической функции, для которой составлена таблица 3.1. Образовав дизъюнкции импликант для каждого столбца импликантной таблицы и объединив их знаком конъюнкции, получим логическое выражение
Ф=  .
.
Преобразуем это выражение к виду
Ф=  .
.
Каждая конъюнкция этого выражения соответствует приведенной системе простых импликант логической функции. Переходя к аналитической форме записи простых импликант, получим все тупиковые формы логической функции.
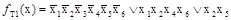 ;
;
 ;
;
 ;
;
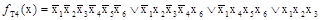 .
.
Сравним полученные тупиковые ДНФ функции найдем ее минимальную ДНФ:
 .
.
Пример 3.10.Определим минимальную КНФ логической функции, заданной имплицентной таблицей 3.2.
Таблица 3.2
Имплицентная таблица к примеру 3.10
| Простые | Единичные наборы | |||
| имплиценты | ||||
| A `x1 Ú x3 Ú`x4 | * | |||
| B x1 Ú `x3 Ú`x4 | * | |||
| C `x2 Ú x4 | * | * | ||
| D `x1 Ú`x2 | * | * | ||
| E `x2 Ú`x3 | * | * |
Для отыскания всех тупиковых КНФ логической функции по имплицентной таблице составим логическое выражение и преобразуем его:
Ф= 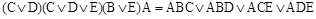 .
.
Каждая конъюнкция этого выражения содержит в качестве сомножителей имплиценты, составляющие приведенную систему.
Тупиковые КНФ функции имеют вид:
 ;
;
 ;
;
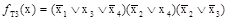 ;
;
 .
.
Сравнив полученные тупиковые КНФ логической функции по числу букв, убедимся, что она имеет две минимальные формы:  и
и  .
.
С увеличением числа переменных, от которых зависит функция, существенно возрастает число тупиковых форм, которое может исчисляться сотнями и тысячами. В связи с этим для таких функций весьма трудоемкой становится задача отыскания минимальных ДНФ (КНФ), требующая определения всех тупиковых ДНФ (КНФ) функции.
Для сокращения объема вычислений в этих случаях нередко отказываются от точного решения задачи минимизации и ограничиваются определением одной или нескольких тупиковых форм, близких к минимальной форме. С этой целью используется приближенный метод исследования импликантных (имплицентных) таблиц, который существенно сокращает объем вычислений и вместе с тем позволяет определить тупиковую форму функции, близкую к минимальной [3,3].
ВЫВОДЫ К ГЛАВЕ 3
1. Алгебра логики или булева алгебра содержит систему правил и аксиом, позволяющих производить эквивалентные преобразования логических функций, представленных в аналитической форме. При выполнении этих преобразований необходимо строго учитывать приоритетность операций дизъюнкции, конъюнкции, отрицания, скобки, стоящие в выражении и появляющиеся после преобразования.
2. Аналитические нормальные формы представления логических функций с точки зрения их избыточности могут быть выстроены в следующую цепочку в порядке уменьшения избыточности : совершенная ДНФ (КНФ), ДНФ (КНФ), сокращенная ДНФ (КНФ), тупиковая ДНФ (КНФ), минимальная ДНФ (КНФ).
3. Существует большое число методов минимизации логических функций, отличающихся исходной формой представления, схемой преобразования и формой представления результата. Область целесообразного применения методов минимизации, позволяющих вручную получить абсолютно минимальные ДНФ или КНФ логических функций (методы карт Карно, решетки соседних чисел, таблично-аналитический метод и др.), ограничивается функциями, зависящими от 5-6 переменных. Для решения задач минимизации функций большего числа переменных могут быть использованы метод поразрядного сравнения [3.3] или машинные алгоритмы реализации различных методов.
Дата добавления: 2022-02-05; просмотров: 652;











