Основные допущения, принимаемые при построении теории автоматов

Цифровые автоматы преобразуют сигналы, которые квантованы как по уровню, так и по времени. Следовательно, и сами цифровые автоматы могут изменять свое состояние только в дискретные моменты времени. Для описания функционирования цифровых автоматов вводится шкала дискретного или автоматного времени, единицей измерения которого является такт.

Тактом работы цифрового автомата называется отрезок времени произвольной длительности, в течение которого состояние автомата остается неизменным.

Такты работы цифрового автомата с памятью делятся на устойчивые и неустойчивые.

Такт называется устойчивым, если очередное изменение состояния цифрового автомата происходит только за счет изменения состояния входов или, другими словами, только после поступления нового входного набора.

Такт называется неустойчивым, если очередное изменение состояния цифрового автомата происходит только за счет изменения состояния памяти автомата.

Из приведенных определений следует, что устойчивый такт всегда предшествует моменту изменения входного набора автомата, а неустойчивый такт - моменту изменения состояния памяти автомата.

Тактам работы автомата, начиная с нулевого, присваиваются порядковые номера, и полученная таким образом последовательность тактов образует дискретное или автоматное время: 0, 1, 2, 3, ..., i, ... При этом следует еще раз подчеркнуть, что реальная длительность тактов может быть произвольной.

При построении теории цифровых автоматов принимают следующие основные допущения.

1. Переход цифрового автомата из одного внутреннего состояния в другое осуществляется скачкообразно.

2. После перехода цифрового автомата в произвольное внутреннее состояние переход в следующее состояние оказывается возможным не ранее чем через некоторый фиксированный для данного автомата промежуток времени 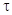>0 - так называемый интервал дискретности автомата.

Скачкообразность перехода означает, что переход автомата из одного состояния в другое происходит мгновенно, минуя какие-либо промежуточные состояния. В любом реальном автомате имеет место конечная длительность переходных процессов, так что требование скачкообразности перехода в полной мере никогда не удовлетворяется. Удовлетворение этого требования оказывается возможным лишь на определенной ступени абстракции. Такая абстракция, однако, достаточно хорошо описывает основные свойства реальных устройств и принимается для построения теории цифровых автоматов.

Допущение о том, что после перехода автомата в произвольное состояние переход в следующее состояние оказывается возможен через некоторый фиксированный для данного автомата промежуток времени, позволяет рассматривать функционирование автомата в дискретном времени. Это допущение также хорошо согласуется с действительностью и отражает тот факт, что пока в цифровом автомате не закончится переходной процесс, связанный с предыдущим изменением его состояния, ни один из входных сигналов не может изменить своего значения. Это допущение соответствует ограничению по быстродействию, которое всегда имеет место в реальных устройствах.