Понятие о цифровом автомате

Автомат - это устройство, выполняющее некоторый процесс без непосредственного участия человека. Слово автомат происходит от греческого 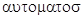-самодействующий.

Цифровой автомат (ЦА) - это математическая модель реального (технического) устройства, служащего для преобразования цифровой информации.

В общем случае ЦА имеет n входов x₁, x₂, ..., x_nи m выходов z₁, z₂, ...,z_m (рис.1.1,а), каждый из которых может принимать некоторое конечное число дискретных значений. Число входов и выходов цифрового автомата конечно. Входы x₁, x₂, ..., x_n образуют множество входов цифрового автомата:

X={x₁, x₂, ...,x_n}.

Выходы z₁, z₂, ...,z_m образуют множество выходов цифрового автомата:

Z={z₁, z₂, ...,z_m}.

Зависимость между выходными и входными сигналами в цифровом автомате реализуется с помощью соединения элементов, которые принято называть логическими.

В цифровых автоматах могут присутствовать элементы, которые, изменяя свое состояние под действием входных сигналов или порождаемых ими управляющих воздействий, после прекращения действия этих сигналов в исходное состояние не возвращаются.

Вторично изменить свое состояние или вернуться в исходное эти элементы могут после воздействия других входных сигналов или повторного воздействия тех же входных сигналов или сигналов ими порождаемых. Такие элементы принято называть элементами памяти (ЭП) цифрового автомата. Типичными представителями элементов памяти являются широко применяемые на практике тригерные устройства различных типов.

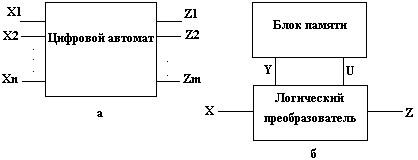
Рис.1.1.

Наличие в цифровом автомате элементов памяти значительно расширяет возможности преобразования информации, при этом могут запоминаться значения входных сигналов, поступающих в предыдущие моменты времени, и использоваться при формировании выходных сигналов.

При решении задач анализа и синтеза цифровых автоматов элементы памяти принято выделять в отдельный блок, который называется блоком памяти или просто памятью цифрового автомата (рис.1.1,б). Часть схемы автомата, не содержащая элементов памяти, называется логическим преобразователем или комбинационным блоком автомата. ЦА, представленный на рис. 1.1,б, получил название канонического автомата или автомата с канонической структурой.

В общем случае блок памяти цифрового автомата может содержать k элементов памяти y₁, y₂, ...,y_k, каждый из которых может принимать некоторое конечное число состояний. Элементы y₁, y₂, ...,y_k образуют множество элементов памяти автомата:

Y={ y₁, y₂, ...,y_k}

Значение переменной y_i будем отождествлять с состоянием обозначаемого этой переменной элемента памяти. Состояние каждого элемента памяти однозначно определяет выходной сигнал, формируемый этим элементом. Поэтому для обозначений сигналов, формируемых элементами памяти, можно использовать те же буквы которые обозначают элементы памяти, а множество Y={ y₁, y₂, ...,y_k } в необходимых случаях будем рассматривать как множество выходов блока памяти автомата.

Логический преобразователь автомата помимо формирования выходных сигналов обеспечивает управление блоком памяти цифрового автомата. Для этого он имеет l выходов управления памятью u₁, u₂, ...,u_l, которые образуют множество выходов управления памятью:

U={u₁, u₂, ...,u_l}.

Выходы логического преобразователя непосредственно соединяются с соответствующими входами блока памяти автомата. Поэтому множество u нередко называют множеством входов управления памятью автомата. В общем случае l 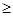k, так как каждый элемент памяти автомата может иметь один или несколько управляющих входов. Так, при построении памяти автомата на RS-триггерах мощность множества u в два раза превышает мощность множества Y, т.е. l=2k. Ввиду простоты технической реализации в настоящее время наибольшее распространение получили цифровые автоматы, сигналы в которых принимают только два возможных значения. При математическом описании таких сигналов, независимо от физической природы, их значения отождествляют с цифрами 0 и 1. В дальнейшем изложении будем рассматривать автоматы, работающие только с двоичными сигналами.

Если каждому входному сигналу автомата присвоить конкретное значение на множестве {0,1}, то полученная совокупность значений входных сигналов будет представлять собой комбинацию значений входных сигналов или входной набор цифрового автомата. В общем виде входной набор цифрового автомата запишется следующим выражением:

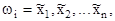
где

Так как каждый входной сигнал цифрового автомата может принимать одно из двух возможных значений независимо от значений других входов, то максимальное число различных входных наборов определяется как произведение, состоящее из n цифр 2, т.е.

N_вх=2ⁿ .

Таким образом, максимальная мощность множества входных наборов цифрового автомата равна 2ⁿ. Множество входных наборов автомата будем записывать в виде

,

где .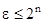

Выходной набор цифрового автомата будем записывать в виде

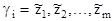
Совокупность выходных наборов образует множество выходных наборов автомата:

,

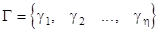где - мощность множества выходных наборов цифрового автомата.

Введем также понятие „набор состояний элементов памяти автомата“, или просто „внутреннее состояние памяти“ („внутреннее состояние“) -

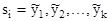
и множество состояний памяти цифрового автомата:

,

где

Отличительной особенностью задания этого множества является нумерация состояний памяти, начиная с состояния S₀, которое выделяется специально для обозначения начального состояния памяти автомата. В связи с этим максимальный номер последнего состояния будет равен 2^k-1, а максимальная мощность множества состояний памяти автомата -2^k

Цифровые автоматы в зависимости от количества состояний памяти делятся на автоматы с одним внутренним состоянием, у которых элементы памяти отсутствуют, и автоматы с двумя и более внутренними состояниями, содержащие один и более элементов памяти.

Цифровые автоматы с двумя и более внутренними состояниями называют цифровыми автоматами с памятью или последовательностями машин. Принципиальным отличительным признаком цифровых автоматов с памятью является то, что значения выходных сигналов (наборы значений выходных сигналов) у них определяются не только значениями входных сигналов (входными наборами), поступившими в этот момент времени, но и их предыдущими значениями, а также порядком их поступления на входы автомата.

Если элементы памяти в схеме автомата отсутствуют, считается, что такой автомат имеет одно внутреннее состояние, которое полностью определяется составом и схемой соединения его элементов. Цифровые автоматы этого типа называют цифровыми автоматами без памяти, комбинационными автоматами или логическими преобразователями. Работа таких автоматов состоит в том, что они сопоставляют каждому входному набору некоторый выходной набор, значение которого полностью определяется значениями входных сигналов, действующих в данный момент времени, и никак не зависит от предшествующих значений состояний входов. Таким образом, цифровой автомат без памяти можно рассматривать как частный случай цифрового автомата с памятью, у которого число внутренних состояний сведено к одному, а элементы памяти отсутствуют. С другой стороны, цифровой автомат с памятью представляет собой совокупность цифрового автомата без памяти и элементов памяти, объединенных в блок памяти автомата. В общем случае выходные сигналы автомата определяются как входными сигналами, так и состояниями элементов памяти автомата, которые в комплексе характеризуют состояние автомата. Для записи состояний автомата будем использовать следующую запись:

,

которая обозначает, что состояние цифрового автомата a_p характеризуется входным набором 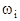и состоянием памяти s_j.

Совокупность состояний a_p образует множество состояний автомата

A={a₁, a₂, ...,a_µ}.

Если допустить, что при каждом входном наборе автомат может находиться в любом из внутренних состояний, то максимальное число состояний цифрового автомата определяется как произведение максимального числа входных наборов на максимальное число его состояний памяти:

N_сост =

Полученное число определяет максимальную мощность множества А и, следовательно, для реальных автоматов . Число состояний µ быстро возрастает с увеличением сложности автомата, числа входов и элементов памяти.