Расчёт точности системы при случайных воздействиях
Рассмотрим расчёт среднеквадратичной ошибки на примере системы, структурная схема которой имеет вид, изображённый на рис. 3.4.


Рис. 3.4
Пусть на вход системы поступают регулярный сигнал 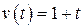 и помеха
и помеха 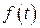 типа “белый шум” со спектральной плотностью
типа “белый шум” со спектральной плотностью 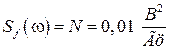 . Параметры передаточной функции:
. Параметры передаточной функции: 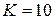 1/с,
1/с, 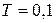 с.
с.
Необходимо определить среднеквадратичную ошибку. Средний квадрат ошибки  , где
, где 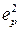 - квадрат регулярной составляющей ошибки, а
- квадрат регулярной составляющей ошибки, а 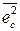 - средний квадрат случайной составляющей ошибки.
- средний квадрат случайной составляющей ошибки.
Составляющая 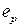 находится по известной формуле:
находится по известной формуле: 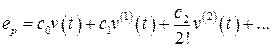 .
.
Коэффициенты ошибок 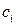 определяются при разложении в ряд Маклорена передаточной функции системы по ошибке
определяются при разложении в ряд Маклорена передаточной функции системы по ошибке 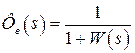 . В нашем случае
. В нашем случае 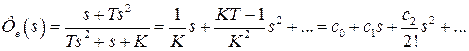 .
.
Так как 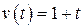 , то надо вычислить лишь первую производную
, то надо вычислить лишь первую производную 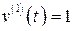 .
.
Следовательно 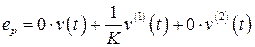 . При учёте численных значений
. При учёте численных значений 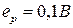 , а
, а 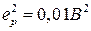 .
.
Определим среднее значение квадрата случайной составляющей 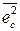 . Как показано в
. Как показано в 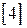
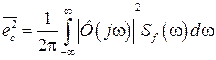 . (3.18)
. (3.18)
Для преодоления трудностей при вычислении интеграла (3.18), его представляют в виде:
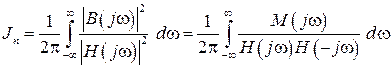 , (3.19)
, (3.19)
где 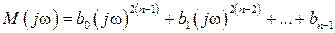 ;
; 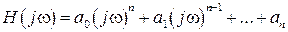 .
.
Формулы для вычисления интегралов по коэффициентам 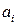 и
и 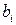 для соответствующих значений
для соответствующих значений 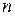 сведены в таблицы. Приведём их для
сведены в таблицы. Приведём их для 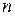 от 1 до 3
от 1 до 3 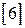 :
:
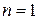 ;
; 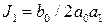 ;
;
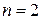 ;
; 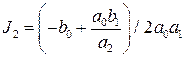 ;
;
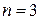 ;
; 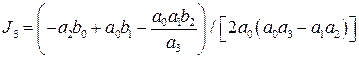 .
.
В нашем случае 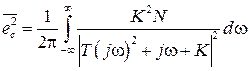 ;
; 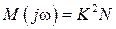 ;
; 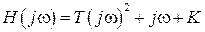 . Коэффициенты:
. Коэффициенты: 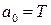 ,
, 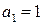 ,
, 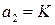 ,
, 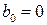 ,
, 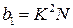 . Интеграл
. Интеграл 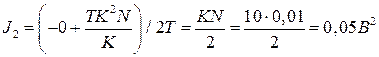 .
.
Среднеквадратичная ошибка 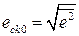 . С учётом численных значений
. С учётом численных значений 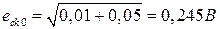 .
.
Дата добавления: 2022-02-05; просмотров: 426;











