Математические модели замкнутых нелинейных систем автоматического управления
Рассмотрим нелинейную САУ, структура которой представлена на рис. 2.2. Пусть линейная часть системы описывается передаточной функцией
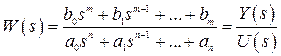 , (2.4)
, (2.4)
используя которую нетрудно получить дифференциальное уравнение, связывающее переменные 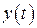 и
и 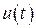
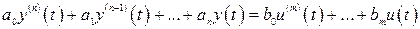 , (2.5)
, (2.5)
где 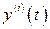 ,
, 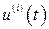 – производные по времени.
– производные по времени.
В соответствии со структурой нелинейной САУ рис. 2.2 нелинейный элемент имеет характеристику 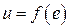 , где
, где 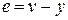 . Итак с учетом (2.5) математической моделью замкнутой нелинейной САУ будет следующая система уравнений
. Итак с учетом (2.5) математической моделью замкнутой нелинейной САУ будет следующая система уравнений
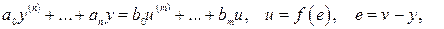 (2.6)
(2.6)
где 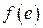 – функция, характеризующая нелинейную зависимость.
– функция, характеризующая нелинейную зависимость.
Другой вариант модели можно получить, используя уравнение состояния [1]. По передаточной функции 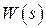 или по дифференциальному уравнению (2.5) можно связать координаты
или по дифференциальному уравнению (2.5) можно связать координаты 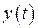 и
и 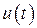 с помощью векторно-матричных уравнений
с помощью векторно-матричных уравнений
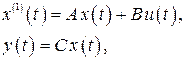 (2.7)
(2.7)
где 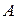 – матрица размерностью
– матрица размерностью 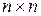 ,
, 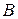 –вектор столбец,
–вектор столбец, 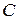 – вектор строка,
– вектор строка, 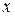 – вектор состояния с координатами
– вектор состояния с координатами 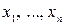 .
.
В этом случае с учетом 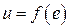 ,
, 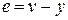 получим векторно-матричную модель или уравнения состояния нелинейной системы
получим векторно-матричную модель или уравнения состояния нелинейной системы
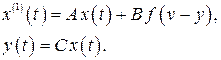 (2.8)
(2.8)
Наконец, иногда рассматривают смешанную модель вида
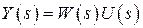 ,
, 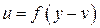 , (2.9)
, (2.9)
где 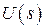 ,
, 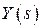 – изображения, а
– изображения, а 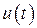 ,
, 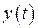 ,
, 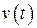 – функции времени (оригиналы).
– функции времени (оригиналы).
Объектом дальнейшего рассмотрения являются модели вида (2.6), (2.8) или (2.9). При этом можно выделить следующие возможные направления исследований:
1. Функция 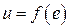 в окрестностях исследуемого режима (обычно это положение равновесия) является достаточно гладкой и допускает линеаризацию (разложение ее в ряд Тейлора). Тогда при достаточно малых отклонениях от установившегося режима уравнения (2.6) и (2.8) заменяются на линеаризованные и исследуются линейными методами [1].
в окрестностях исследуемого режима (обычно это положение равновесия) является достаточно гладкой и допускает линеаризацию (разложение ее в ряд Тейлора). Тогда при достаточно малых отклонениях от установившегося режима уравнения (2.6) и (2.8) заменяются на линеаризованные и исследуются линейными методами [1].
2. Линеаризация в соответствии с пунктом 1 допустима, но отклонения от установившегося режима большие. В этом случае САУ надо рассматривать как нелинейную.
3. Линеаризация по пункту 1 недопустима, особенно в случае разрывных нелинейных характеристик. САУ следует рассматривать только как нелинейную.
Излагаемое далее будет относиться к двум последним случаям.
Методы анализа нелинейных САУ, описываемых нелинейными дифференциальными уравнениями (2.6), (2.8), условно можно разделить на точные и приближенные. В свою очередь и в тех и в других можно выделить аналитические, графические и графоаналитические методы расчета и анализа. Широкие возможности дают методы с использованием компьютерного моделирования.
При исследовании процессов в НСАУ можно выделить два направления: исследование собственных процессов в НСАУ при 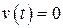 и исследование вынужденных режимов, возникающих при внешних воздействиях
и исследование вынужденных режимов, возникающих при внешних воздействиях 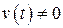 . Кроме этого большое значение имеют задачи, связанные с отысканием периодических режимов, автоколебательных режимов и анализом устойчивости процессов в НСАУ.
. Кроме этого большое значение имеют задачи, связанные с отысканием периодических режимов, автоколебательных режимов и анализом устойчивости процессов в НСАУ.
Пример 2.1. В НСАУ рис. 2.2 линейная часть описывается передаточной функцией 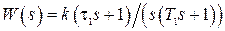 . Найдем математические модели системы. Смешанная форма будет
. Найдем математические модели системы. Смешанная форма будет
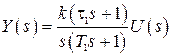 ,
, 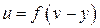 .
.
Уравнения (2.6) имеют вид
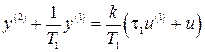 ,
, 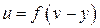 .
.
Используя передаточную функцию 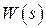 , найдем уравнения состояния линейной части в канонической форме
, найдем уравнения состояния линейной части в канонической форме
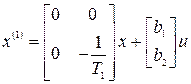 ,
, 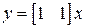 ,
,
где 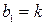 ;
; 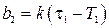 ;
; 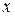 – вектор с координатами
– вектор с координатами 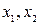 .
.
С учетом уравнения замыкания получим модель (2.7):
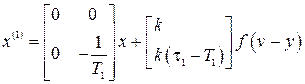 ,
, 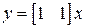 .
.
Дата добавления: 2022-02-05; просмотров: 451;











