Частота единичного усиления двухкаскадного ОИТУН
Как следует из изложенного выше, если 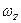 и
и 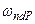 выше
выше 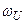 , то при
, то при 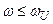 АЧХ многокаскадного ОИТУН должна быть близка к АЧХ системы первого порядка. Для оценки при этом значения
АЧХ многокаскадного ОИТУН должна быть близка к АЧХ системы первого порядка. Для оценки при этом значения 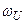 упростим передаточную функцию (4.35) до первого порядка, отбросив член со степенью
упростим передаточную функцию (4.35) до первого порядка, отбросив член со степенью 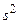 , и из упрощенной передаточной функции определим выражение для
, и из упрощенной передаточной функции определим выражение для 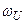 , а также условия (области частот полюса и нуля относительно частоты единичного усиления
, а также условия (области частот полюса и нуля относительно частоты единичного усиления 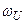 , полученной в предположении, что система имеет порядок, равный единице), при которых поведение системы второго порядка в главных чертах напоминает поведение системы первого порядка.
, полученной в предположении, что система имеет порядок, равный единице), при которых поведение системы второго порядка в главных чертах напоминает поведение системы первого порядка.
Итак, примем передаточную функцию рассматриваемого ОИТУН за функцию первого порядка:
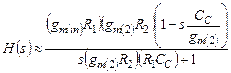 (4.39)
(4.39)
Из (4.39) легко получить выражение для модуля передаточной функции 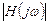 :
:
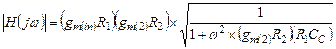 (4.40)
(4.40)
Учитывая, что на частотах, сравнимых с 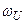 , имеем
, имеем 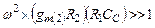 , пренебрежем единицей в знаменателе (4.40) и получаем:
, пренебрежем единицей в знаменателе (4.40) и получаем:
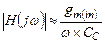 (4.41)
(4.41)
Полагая 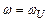 и
и 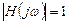 , получаем выражение для
, получаем выражение для 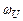 :
:
 (4.42)
(4.42)
Так же, как и в каскодном усилителе, значение 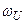 равно отношению крутизны входного транзистора к значению емкости частотной коррекции, входящей в выражение для основного полюса. Из (4.42) следует, что для соблюдения соотношения
равно отношению крутизны входного транзистора к значению емкости частотной коррекции, входящей в выражение для основного полюса. Из (4.42) следует, что для соблюдения соотношения 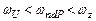 необходимо
необходимо 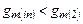 .
.
4.3.6. Устранение нуля в положительной полуплоскости
Нуль в положительной полуплоскости устраняется введением резистора 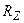 последовательно с
последовательно с 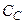 в цепи отрицательной обратной связи второго каскада, как изображено на рис. 4.8.
в цепи отрицательной обратной связи второго каскада, как изображено на рис. 4.8.
На высокой частоте, когда импедансом 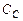 можно пренебречь,
можно пренебречь, 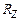 разделяет выходы каскадов, преграждая сквозной путь с выхода D первого каскада на выход усилителя. В этом смысле чем больше номинал
разделяет выходы каскадов, преграждая сквозной путь с выхода D первого каскада на выход усилителя. В этом смысле чем больше номинал 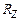 , тем лучше. Однако при увеличении
, тем лучше. Однако при увеличении 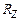 затрудняется перезарядка выходным сигналом через
затрудняется перезарядка выходным сигналом через 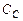 паразитной емкости
паразитной емкости 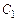 и, таким образом, затвора
и, таким образом, затвора 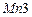 , входного транзистора второго каскада. Последнее также не позволяет транзистору
, входного транзистора второго каскада. Последнее также не позволяет транзистору 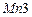 на высокой частоте работать в диодном режиме, из-за чего увеличивается эффективное выходное сопротивление выходного узла.
на высокой частоте работать в диодном режиме, из-за чего увеличивается эффективное выходное сопротивление выходного узла.

Рис. 4.8. Двухкаскадный усилитель без нуля в положительной
полуплоскости.
Все это ведет, во-первых, к появлению комплексных полюсов, и, во-вторых, действительные части этих полюсов становятся меньше. Очевидно, что существует оптимальная величина 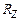 . Найдем эту величину из расчета передаточной функции второго каскада по эквивалентной схеме, приведенной на рис. 4.9.
. Найдем эту величину из расчета передаточной функции второго каскада по эквивалентной схеме, приведенной на рис. 4.9.
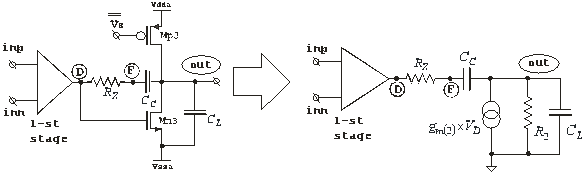
Второй каскад Эквивалентная малосигнальная
двухкаскадного усилителя схема второго каскада
Рис. 4.9. Второй каскад двухкаскадного усилителя с нуль – резистором и эквивалентная малосигнальная схема второго каскада.
Система уравнений Кирхгофа для эквивалентной схемы второго каскада:
(1) 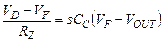 (4.43а)
(4.43а)
(2) 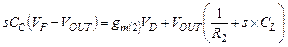 (4.43b)
(4.43b)
Определяем передаточную функцию  относительно узла D:
относительно узла D:
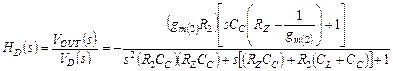 (4.44)
(4.44)
В передаточной функции присутствует нуль с частотой
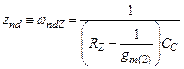 (4.45)
(4.45)
При 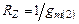 нуль отсутствует. Такая величина
нуль отсутствует. Такая величина 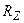 является оптимальной.
является оптимальной.
Расчет передаточной функции всего усилителя (см. рис. 4.8), производится согласно его эквивалентной схемы на рис. 4.10.

Рис. 4.10. Эквивалентная малосигнальная схема двухкаскадного усилителя с нуль – резистором.
Расчет передаточной функции по этой схеме приводит к следующим значениям полюсов и нуля:
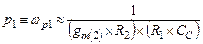 (4.46а)
(4.46а)
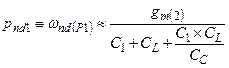 (4.46b)
(4.46b)
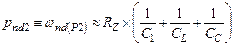 (4.46с)
(4.46с)
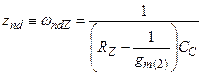 (4.46d)
(4.46d)
При 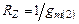 нуль отсутствует. Полюс
нуль отсутствует. Полюс 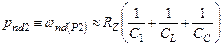 имеет очень высокую собственную частоту, т.к. емкость в составе этого действительного полюса равна последовательному соединению
имеет очень высокую собственную частоту, т.к. емкость в составе этого действительного полюса равна последовательному соединению 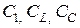 и, разумеется, меньше
и, разумеется, меньше 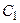 , паразитной емкости на выходе первого каскада. Физически полюс
, паразитной емкости на выходе первого каскада. Физически полюс 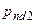 определяется цепоской
определяется цепоской 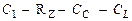 перезарядки последовательно соединенных
перезарядки последовательно соединенных 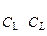 и
и 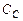 через резистор
через резистор 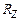 (см. рис. 4.8).
(см. рис. 4.8).
Принципиально возможно, несколько увеличив 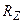 относительно величины
относительно величины 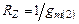 , сместить нуль в отрицательную полуплоскость и установить его частоту, равной частоте первого неосновного полюса
, сместить нуль в отрицательную полуплоскость и установить его частоту, равной частоте первого неосновного полюса 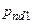 для взаимной компенсации полюса и нуля. Для этого выражение (3 – 16) следует приравнять к выражению (3 – 17в) и из полученного уравнения определить
для взаимной компенсации полюса и нуля. Для этого выражение (3 – 16) следует приравнять к выражению (3 – 17в) и из полученного уравнения определить 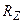 :
:
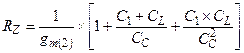 (4.46е)
(4.46е)
Такой заманчивой возможностью, однако, следует пользоваться с осторожностью, а, может быть, и совсем не пользоваться. Дело в том, что точно одинаковыми частоты полюса и нуля не будут никогда из – за естественного разброса номиналов компонентов и, особенно, недостаточной точностью установления требуемой величины 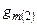 . Близко расположенные частоты дублета полюс – нуль в переходном процессе при наличии отрицательной обратной связи (а ОУ и ОИТУН всегда используются с в схемах с обратной связью) имеет следствием экспоненциальную составляющую с большой постоянной времени, определяемой разностью частот полюса и нуля. Целесообразно все же сместить нуль в отрицательную полуплоскость, но выбрать его частоту такой, чтобы разность частот полюса и нуля при всех разбросах значений параметров в выражении (4.46е) была больше
. Близко расположенные частоты дублета полюс – нуль в переходном процессе при наличии отрицательной обратной связи (а ОУ и ОИТУН всегда используются с в схемах с обратной связью) имеет следствием экспоненциальную составляющую с большой постоянной времени, определяемой разностью частот полюса и нуля. Целесообразно все же сместить нуль в отрицательную полуплоскость, но выбрать его частоту такой, чтобы разность частот полюса и нуля при всех разбросах значений параметров в выражении (4.46е) была больше 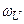 . При этом «медленная» экспонента будет достаточно «быстрой» и во время переходного процесса уменьшится до безопасно малой величины.
. При этом «медленная» экспонента будет достаточно «быстрой» и во время переходного процесса уменьшится до безопасно малой величины.
Дата добавления: 2022-02-05; просмотров: 521;











