Эквивалентная малосигнальная схема двухкаскадного усилителя
На рис. 4.5 приведена эквивалентная малосигнальная схема 2-х каскадного усилителя. В этой схеме добавлен паразитный элемент – паразитная ёмкость 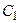 на выходе 1 – го каскада (узел D), равная сумме:
на выходе 1 – го каскада (узел D), равная сумме:
– n+p и p+n областей стоков 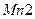 и
и 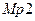 соответственно;
соответственно;
– ёмкостей затвор – сток 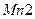 и
и 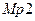 ;
;
– ёмкости затвор – исток 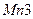 (ёмкость затвор – сток
(ёмкость затвор – сток 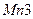 параллельна
параллельна 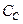 и входит в её состав).
и входит в её состав).

Рис. 4.5. Эквивалентнаямалосигнальная схема двухкаскадного усилителя
По умолчанию предполагается, что паразитная ёмкость на выходе второго каскада входит в состав суммарной емкости 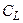 . Паразитная составляющая
. Паразитная составляющая 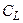 равна сумме (А) паразитных емкостей n+p и p+n областей стоков
равна сумме (А) паразитных емкостей n+p и p+n областей стоков 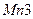 и
и 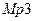 соответственно и (В) емкостей затвор-сток транзисторов
соответственно и (В) емкостей затвор-сток транзисторов 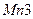 и
и 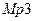 .
.
На эквивалентной схеме:
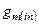 – крутизна по затвору входного транзистора дифкаскада;
– крутизна по затвору входного транзистора дифкаскада;
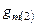 – крутизна по затвору входного транзистора второго каскада;
– крутизна по затвору входного транзистора второго каскада;
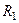 – выходное сопротивление в узле D на выходе первого каскада;
– выходное сопротивление в узле D на выходе первого каскада;
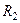 – выходное сопротивление в узле OUT на выходе второго каскада.
– выходное сопротивление в узле OUT на выходе второго каскада.
Как показано в главе 3, малосигнальная эквивалентная схема дифференциального каскада идентична оной для простейшего (базового) усилительного каскада и имеет такой же низкочастотный коэффициент усиления:
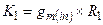 (4.28)
(4.28)
Здесь и далее: 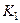 – низкочастотный коэффициент усиления первого каскада, а
– низкочастотный коэффициент усиления первого каскада, а 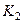 – второго каскада.
– второго каскада.
Второй каскад представляет собой простейший базовый усилительный каскад, поэтому также
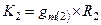 (4.29)
(4.29)
На низких частотах никакие конденсаторы себя не проявляют, поэтому низкочастотный коэффициент усиления 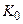 двухкаскадного усилителя равен:
двухкаскадного усилителя равен:
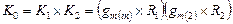 (4.30)
(4.30)
С увеличением частоты импеданс 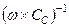 конденсатора
конденсатора 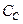 уменьшается, так что сток и затвор транзистора
уменьшается, так что сток и затвор транзистора 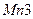 можно считать закороченными. При этом выходное сопротивление узла выхода становится близким к
можно считать закороченными. При этом выходное сопротивление узла выхода становится близким к 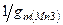 .
.
Этот эффект наблюлается на достаточно высоких частотах, но ведь и фазовый сдвиг на выходе усилителя нас интересует именно на высоких частотах. Итак, неосновной полюс 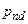 можно предположить известным:
можно предположить известным:
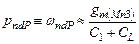 (4.31)
(4.31)
В целях простоты оценки в (4.31) не учтена связь емкостей 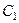 и
и 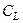 через конденсатор
через конденсатор 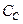 .
.
Для оценки основного полюса 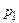 отметим, что
отметим, что 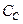 является емкостью Миллера, на которую нагружен источник напряжения, представляемый первым каскадом и имеющим большое выходное сопротивление
является емкостью Миллера, на которую нагружен источник напряжения, представляемый первым каскадом и имеющим большое выходное сопротивление 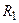 . Это дает основание предположить, что
. Это дает основание предположить, что
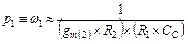 (4.32)
(4.32)
Очевидно, что 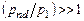 .
.
Дата добавления: 2022-02-05; просмотров: 531;











