Передаточная функция простейшего каскодного усилителя с идеальной токовой нагрузкой

Определим передаточную функцию и ее полюса для простейшего каскодного усилителя, малосигнальная эквивалентная схема которого изображена на рис. 3.21(b). Определим также зависимость полюсов от выходных параметров узлов.

Имеем систему уравнений (с целью сокращения записи полагаем ; ; ; ; ):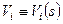

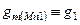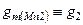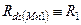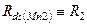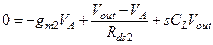(3.74а)

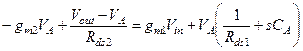(3.74b)

Получаем передаточную функцию:

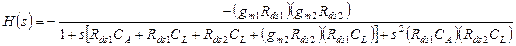(3.75)

Оценим, являются ли полюса передаточной функции действительными. Для этого необходимо определить знак дискриминанта квадратичного многочлена в знаменателе выражения (3.75). Легко, однако, видеть, что даже без учета неравенства 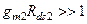, дискриминант положителен, т.е. полюса действительны.

Учитывая неравенство 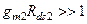, выражение (3.75) можно упростить:

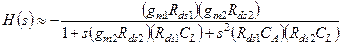(3.76)

Легко видеть, что дискриминант упрощенного выражения (3.76) для передаточной функции (3.75) также положителен.

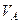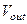Запишем знаменатель последнего выражения в виде, содержащем обозначения действительных полюсов (поскольку схема содержит ДВА узла с неизвестными потенциалами и , то полюсов – также ДВА):

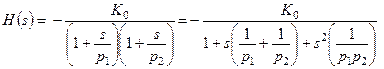(3.77)

Здесь 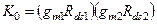– максимальный коэффициент усиления на низких частотах, а 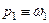и 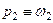– круговые частоты действительных полюсов. Поскольку оба полюса являются действительными, числовое значение полюса, определяемого выходным сопротивлением каскада, легко можно предсказать: 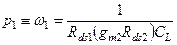, где 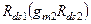— выходное сопротивление в выходном узле 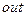усилителя.

Легко видеть, что ввиду большого значения выходного сопротивления каскодного усилителя, собственная частота 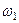первого полюса является очень низкой. В литературе принято самый низкочастотный полюс называть основным (dominant pole). Прочие полюса называют неосновными (nondominant poles).

При оценке собственной частоты второго, неосновного полюса, отметим, что параметры этого полюса определяются параметрами узла А, так как больше узлов в анализируемой схеме на рис. 3.21 нет. Поскольку узел А находится в истокетранзистора Mn2, то справедливо предположить, что активное выходное сопротивление в нем небольшое, по крайней мере близкое к величине 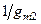выходного сопротивления истокового повторителя. По этой причине выходное сопротивление каскада, равное 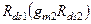, много больше величины 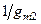, и, следовательно, собственная частота неосновного полюса также много больше собственной частоты основного полюса. Последнее утверждение тем более справедливо при учете очевидного неравенства 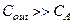(Оценка величины паразитной емкости 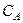приводится ниже в Приложении). Поскольку, как ожидается, 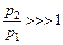, то в (3.77) можно записать:

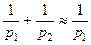(3.78)

Итак, из (3.76) и (3.77) сразу имеем: 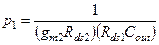(3.79)

Далее, поскольку 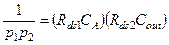, а параметр 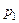известен, то получаем, как и ожидали, 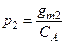, (3.80)

Приложение.Задача 3.2. Оценить величину паразитной емкости 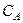между затворами входного и каскодного транзисторов на рис. 3.21.

Оценку проведем согласно топологии входного и каскодного транзисторов на рис. 3.22.

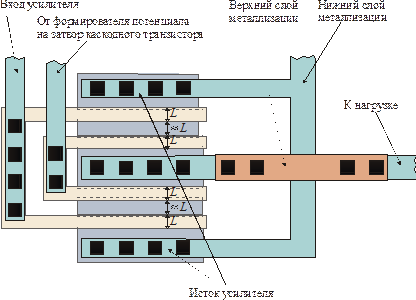
Рис. 3.22. Близкая к оптимальной топология входного и каскодного

транзисторов в простейшем каскодном усилителе с общим истоком.

Поскольку узел А непосредственно не соединен ни с каким-либо узлом, в топологии усилителя отсутствуют контакты к диффузионной области между затворами входного и каскодного транзисторов. Вследствие этого расстояние между затворами целесообразно сделать минимальным. Обычно это расстояние – порядка минимальной длины затвора .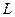

Параметры узла А:

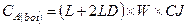(3.81а)

– емкость дна pn-перехода диффузионной области между затворами;

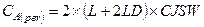(3.82b)

– емкость по периметру диффузионной области (только на границе с фоновым окислом с охранной областью);

В выражениях (3.81a) и (3.81b):

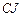– удельная емкость дна pn-перехода на единицу площади; 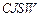– удельная емкость pn-перехода между диффузионной и охранной областями на единицу длины.

Кроме (3.81) и (3.82) в состав паразитной емкости узла А входят:

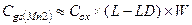(3.82с)

– емкость затвор-исток транзистора M2;

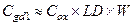(3.82d)

– емкость затвор-сток транзистора M1.

В выражениях (3.81c) и (3.81d):

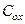– удельная емкость подзатворного диэлектрика.

Поскольку в подавляющем числе случаев ширины транзисторов M1 и M2 одинаковы, то 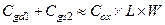– емкость затвора либо транзистора M1, либо транзистора M2.

Оценка отношения суммарной емкости 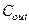в узле out к суммарной паразитной емкости 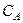узла А составляет, как правило, несколько десятков. Этот результат означает, что задержка во времени, вызванная фактом наличия паразитной емкости 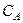узла А, а, следовательно, и задержка фазы, пренебрежимо малы в сравнении с задержками, связанными с емкостью 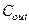в выходном узле. Последнее позволяет сделать выводы:

– фаза выходного сигнала каскодного усилителя мало отличается от фазы 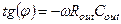(см. выражение (3.14)) простейшего усилителя с общим истоком;

– частота 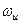единичного усиления простейшего каскодного усилителя мало отличается от частоты 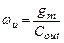простейшего усилителя (см. выражение (3.23)) с общим истоком.

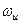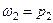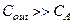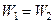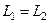– существует очень важное и благоприятное соотношение между частотой единичного усиления простейшего каскодного усилителя и частотой неосновного полюса. Поскольку , и , то

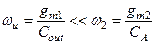(3.83)

Выражение (3.83) означает, что АЧХ и ФЧХ каскодного усилителя в области частот от 0 Гц до частоты 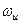единичного усиления таковы, что при малом сигнале на входе каскодный усилитель в этой самой важной области частот можно считать системой первого порядка.