Метод увеличения выходного сопротивления усилителя
Базовый усилительный каскад (сейчас и в дальнейшем будем по умолчанию подразумевать каскад с активной нагрузкой) содержит транзисторы обоих типов проводимости, и для увеличения его коэффициента усиления 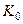 необходимо найти метод увеличения выходных сопротивлений
необходимо найти метод увеличения выходных сопротивлений 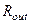 транзисторов обоих типов. Метод будем иллюстрировать на примере транзисторов одного типа (например, N-типа). Для исключения влияния на результат транзисторов нагрузки другого, типа заменим реальную нагрузку идеальным источником тока.
транзисторов обоих типов. Метод будем иллюстрировать на примере транзисторов одного типа (например, N-типа). Для исключения влияния на результат транзисторов нагрузки другого, типа заменим реальную нагрузку идеальным источником тока.
На рис. 3.20а изображен усилительный каскад, где в исток входного транзистора помещен резистор 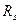 .
.
Будем рассматривать выходное сопротивление 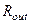 каскада на низких частотах (в пределе – на постоянном токе), когда влиянием всех емкостей можно пренебречь, и параметр
каскада на низких частотах (в пределе – на постоянном токе), когда влиянием всех емкостей можно пренебречь, и параметр 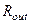 неизбежно оказывается действительным. Эквивалентная малосигнальная схема усилительного каскада с резистором в истоке приведена на рис. 3.17b.
неизбежно оказывается действительным. Эквивалентная малосигнальная схема усилительного каскада с резистором в истоке приведена на рис. 3.17b.

(а) (b)
Рис. 3.20. Усилительный каскад с резистором  в истоке входного транзистора
в истоке входного транзистора 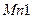 и с источником постоянного режимного тока
и с источником постоянного режимного тока 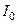 в качестве нагрузки: (а) электрическая схема; (b) малосигнальная эквивалентная схема для расчета низкочастотного активного выходного сопротивления
в качестве нагрузки: (а) электрическая схема; (b) малосигнальная эквивалентная схема для расчета низкочастотного активного выходного сопротивления 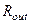
( 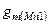 и
и 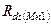 – соответственно крутизна по затвору и дифференциальное сопротивление сток – исток в пологой области транзистора
– соответственно крутизна по затвору и дифференциальное сопротивление сток – исток в пологой области транзистора 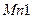 ).
).
Согласно малосигнальной эквивалентной схеме каскада, составляем два
уравнения Кирхгофа (по количеству узлов в схеме). В целях упрощения анализа, пренебрегаем влиянием общей подложки, поскольку, во-первых, ее учет не вносит принципиально новых эффектов и, во-вторых, крутизна 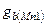 по подложке в несколько раз меньше крутизны
по подложке в несколько раз меньше крутизны 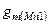 по затвору.
по затвору.
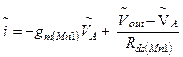 (3.69а)
(3.69а)
 (3.69b)
(3.69b)
Решая систему, получаем:
 (3.70)
(3.70)
Видно, что выходное сопротивление каскада с общим истоком после включения резистора 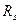 в исток входного транзистора цепь резистора увеличилось по сравнению с
в исток входного транзистора цепь резистора увеличилось по сравнению с 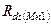 не просто на величину
не просто на величину 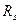 , а более, чем в
, а более, чем в 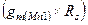 раз.
раз.
Физическое объяснение эффекта следующее. При увеличении выходного напряжения 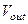 , т.е. напряжения сток-исток
, т.е. напряжения сток-исток 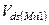 транзистора в пологой области, ток
транзистора в пологой области, ток 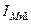 в нем растет. Однако при этом увеличивается напряжение
в нем растет. Однако при этом увеличивается напряжение  на резисторе
на резисторе 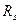 и, соответственно, растет потенциал истока
и, соответственно, растет потенциал истока 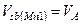 . Поскольку, при расчете выходного сопротивления схемы на рис. 3.17, напряжение на затворе
. Поскольку, при расчете выходного сопротивления схемы на рис. 3.17, напряжение на затворе  входного транзистора
входного транзистора 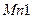 по определению постоянно, то уменьшается превышение над порогом
по определению постоянно, то уменьшается превышение над порогом  . Последнее означает, что ток в пологой области через транзистор
. Последнее означает, что ток в пологой области через транзистор 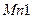 растет в меньшей степени, чем при отсутствии
растет в меньшей степени, чем при отсутствии 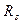 .
.
Очевидно, что для увеличения 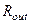 необходимо увеличивать
необходимо увеличивать 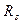 , но при этом неизбежно уменьшается режимный ток, крутизна
, но при этом неизбежно уменьшается режимный ток, крутизна 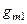 транзистора и, соответственно, уменьшается быстродействие каскада. Покажем, что при этом в схеме на рис. 3.17а, несмотря на увеличение
транзистора и, соответственно, уменьшается быстродействие каскада. Покажем, что при этом в схеме на рис. 3.17а, несмотря на увеличение 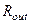 , усиление не увеличивается. Это утверждение достаточно очевидно, поскольку ток во входном транзисторе
, усиление не увеличивается. Это утверждение достаточно очевидно, поскольку ток во входном транзисторе 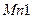 является также током в резисторе
является также током в резисторе  и, поэтому, определяется не только крутизной транзистора, но и сопротивлением в его истоке.
и, поэтому, определяется не только крутизной транзистора, но и сопротивлением в его истоке.
Приложение. Задача 3.1.
Подтвердим рассуждения в последнем абзаце прямым расчетом коэффициента усиления схемы на рис. 3.17 и определим эффективную (т.е. сниженную) крутизну входного транзистора 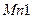 , при которой усиление, как ожидается, получится низким.
, при которой усиление, как ожидается, получится низким.
Уравнения Кирхгофа для схемы на рис. 3.17:
 (П3.1)
(П3.1)
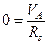 (П3.2)
(П3.2)
Решая систему (), получаем:  (П3.3)
(П3.3)
Как видно из (П3.3), коэффициент усиления усилителя 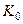 с идеальной токовой нагрузкой и резистором в истоке идентичен коэффициенту усиления усилителя без резистора. Формально, согласно выражению (), это следует из равенства
с идеальной токовой нагрузкой и резистором в истоке идентичен коэффициенту усиления усилителя без резистора. Формально, согласно выражению (), это следует из равенства 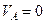 , т.е. узел А проявляет себя как источник постоянного напряжения.
, т.е. узел А проявляет себя как источник постоянного напряжения.
Перепишем выражение (П3.3), умножив и разделив его на 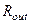 из (3.70):
из (3.70):
 (П3.4))
(П3.4))
Здесь 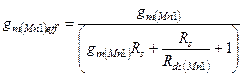 (П3.5))
(П3.5))
Как видно из (), эффективная крутизна транзистора уменьшилась в такой же мере, в какой увеличилось выходное сопротивление, и коэффициент усиления остался таким же, как при отсутствии резистора  . При
. При 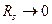 эффективная крутизна транзистора максимальна и равна
эффективная крутизна транзистора максимальна и равна 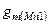 , однако выходное сопротивление каскада минимально и равно
, однако выходное сопротивление каскада минимально и равно 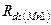 .
.
Дата добавления: 2022-02-05; просмотров: 565;











