Не чувствительный к паразитным емкостям
На рис. 1.12 представлена концепция переключаемого конденсатора, также не чувствительного к паразитным емкостям, но, во-первых, инвертирующего знак заряда, пришедшего в его левую обкладку при подключении к входному сигналу и, во-вторых, с задержкой. Пусть для определенности 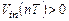 .
.
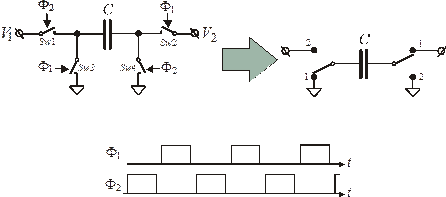
Рис. 1.13. Инвертирующий переключаемый конденсатор с задержкой, нечувствительный к паразитным емкостям.
Конфигурация цепей на рис. 1.13 идентична конфигурации на рис. 1.11 для неинвертирующего ПК без задержки. Различие состоит во взаимном обмене тактовыми сигналами между ключами Sw1 и Sw3.
Перед тем, как приступить к анализу инвертирующего ПК на рис. 1.13, напоминаем, что в целях упрощения анализа ключи предполагаются идеальными. Идеальность ключей заключается не только в отсутствии их сопротивления в замкнутом состоянии и в полном разрыве цепи в разомкнутом состоянии. Предположим теперь, что при размыкании ключа отсутствует паразитная инжекция заряда инверсионного слоя канала МДП транзистора (см. описания аналоговых ключей в главах II и VI). Для появления тока в МДП транзисторе под затвором требуется индуцировать инверсионный зарядовый слой, а для прекращения тока требуется, чтобы эти заряды из канала исчезли. Исчезать же («инжектироваться») из канала они могут практически только в диффузионные области стока и истока МДП ключа, изменяя заряды узлов, к которым присоединены эти сток и исток и, соответственно, изменяя потенциалы этих узлов. В подавляющем множестве случаев эффект изменения потенциалов узлов, оставшихся плавающими после размыкания ключа, является вредным, т.е. паразитным. Причиной такого утверждения является зависимость заряда инжекции от величины аналогового сигнала на входе ключа, что приводит к нелинейности цепи на базе ПК. Ниже, в главе VI, описываются методы уменьшения (к сожалению – не устранения, поскольку последнее невозможно) нежелательных последствий от паразитной инжекции.
Ниже описывается последовательность событий в схеме на рис. 1.13.
(А) Такт слежения за входным сигналом от 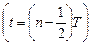 до
до 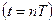 . Состояние тактовых сигналов при этом: Ф2 =1 и Ф1 =0.
. Состояние тактовых сигналов при этом: Ф2 =1 и Ф1 =0.
Ключи, Sw3 и Sw4 замкнуты, а ключи и Sw2 – разомкнуты. При этом конденсатор 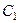 заряжается, т.е. потенциал левой обкладки равен входному в момент времени
заряжается, т.е. потенциал левой обкладки равен входному в момент времени 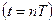 , а правой – равен нулевому потенциалу аналоговой земли. В момент
, а правой – равен нулевому потенциалу аналоговой земли. В момент 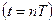 размыкания ключей Sw1 и Sw4 верхняя обкладка переключаемого конденсатора
размыкания ключей Sw1 и Sw4 верхняя обкладка переключаемого конденсатора 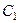 заряжена положительным зарядом
заряжена положительным зарядом
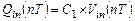 (1.43)
(1.43)
Этот момент называют моментом выборки, поскольку на конденсаторе 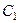 после момента времени
после момента времени 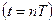 хранится заряд
хранится заряд 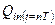 , однозначно соответствующий входному потенциалу в этот момент.
, однозначно соответствующий входному потенциалу в этот момент.
(В) Рабочий такт от 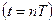 до
до 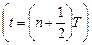 . Состояние тактовых сигналов: Ф1 =1 и Ф2 =0, т.е. ключи, Sw3 и Sw2 замкнуты, а ключи Sw1 и Sw4 – разомкнуты.
. Состояние тактовых сигналов: Ф1 =1 и Ф2 =0, т.е. ключи, Sw3 и Sw2 замкнуты, а ключи Sw1 и Sw4 – разомкнуты.
Если, как для определенности условлено выше, 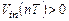 , то в этот промежуток времени левая обкладка переключаемого конденсатора
, то в этот промежуток времени левая обкладка переключаемого конденсатора 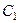 разряжается до нуля, т.е. изменение потенциала на этой обкладке имеет отрицательный знак , и, очевидно, по абсолютной величине равно входному потенциалу
разряжается до нуля, т.е. изменение потенциала на этой обкладке имеет отрицательный знак , и, очевидно, по абсолютной величине равно входному потенциалу 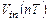 . Соответственно, в левую обкладку конденсатора
. Соответственно, в левую обкладку конденсатора 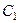 входит отрицательный заряд, по абсолютной величине равный положительному заряду
входит отрицательный заряд, по абсолютной величине равный положительному заряду 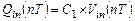 . Такой же отрицательный заряд «выталкивается» через ключ Sw2 в источник
. Такой же отрицательный заряд «выталкивается» через ключ Sw2 в источник 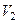 :
:
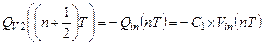 (1.44)
(1.44)
Как очевидно из (1.44), рассматриваемый конденсатор, представленный на рис. 1.13, является инвертирующим и с задержкой.
Что касается паразитных емкостей, то все, что о них было изложено в разделе о не инвертирующем ПК без задержки, от этих емкостей не зависящем, справедливо и для рассматриваемого инвертирующего ПК с задержкой.
1.5.5. Неинвертирующий ПК интегратор с задержкой
На рис. 1.14 представлена схема неинвертирующего интегратора с задержкой на базе инвертирующего ПК с задержкой. Рассматриваемый интегратор является неинвертирующим, поскольку состоит из инвертирующего ПК, подключенному к инвертирующему же входу операционного усилителя (ОУ).
Согласно (1.42), в момент времени 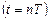 из правой обкладки конденсатора
из правой обкладки конденсатора 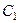 через ключ Sw2 в узел А инвертирующего входа ОУ вносится заряд, равный
через ключ Sw2 в узел А инвертирующего входа ОУ вносится заряд, равный 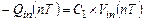 . Если
. Если 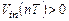 , то привнесенный в узел А заряд изменяет потенциал узла в отрицательную сторону и, соответственно, потенциал выходного узла
, то привнесенный в узел А заряд изменяет потенциал узла в отрицательную сторону и, соответственно, потенциал выходного узла 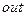 изменяется в положительную сторону. При этом в правую обкладку инвертирующего конденсатора
изменяется в положительную сторону. При этом в правую обкладку инвертирующего конденсатора 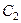 вносится положительный заряд, и такой же положительный заряд «выталкивается» из левой обкладки в узел А, компенсируя находящийся там отрицательный заряд, «вытолкнутый» из левой обкладки
вносится положительный заряд, и такой же положительный заряд «выталкивается» из левой обкладки в узел А, компенсируя находящийся там отрицательный заряд, «вытолкнутый» из левой обкладки 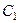 .
.
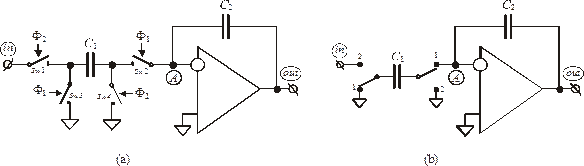
Рис. 1.14. Неинвертирующий ПК интегратор с задержкой:
(а) с подробным изображением ключей; (b) с условными перекидными
ключами
При идеальных ключах и ОУ процессы компенсации и установления соответствующего потенциала на выходе интегратора происходят мгновенно, т.е. уже непосредственно в момент времени 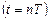 выходной потенциал заканчивает изменяться на величину, достаточную для компенсации зарядов в узле А. В реальности процесс компенсации проходит за промежуток времени, равный половине периода, от
выходной потенциал заканчивает изменяться на величину, достаточную для компенсации зарядов в узле А. В реальности процесс компенсации проходит за промежуток времени, равный половине периода, от 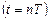 до
до 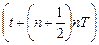 , пока узел А еще отрицателен относительно неинвертирующего входа ОУ. При положительном изменении выходного потенциала и сравнивании потенциалов обоих входов ОУ (при отсутствии смещения нуля в идеальном ОУ), величина положительного заряда величины
, пока узел А еще отрицателен относительно неинвертирующего входа ОУ. При положительном изменении выходного потенциала и сравнивании потенциалов обоих входов ОУ (при отсутствии смещения нуля в идеальном ОУ), величина положительного заряда величины
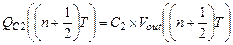 , (1.45)
, (1.45)
«вытолкнутого» из левой обкладки конденсатора 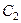 , сравнивается с величиной отрицательного заряда, «вытолкнутого» из правой обкладки
, сравнивается с величиной отрицательного заряда, «вытолкнутого» из правой обкладки 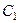 и равного
и равного
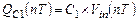 (1.46)
(1.46)
Таким образом, для изменения напряжения на выходе ПК интегратора с задержкой можно записать:
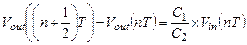 (1.47а)
(1.47а)
Поскольку в промежуток времени от 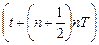 до
до 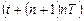 ключ Sw2 разомкнут и левая обкладка конденсатора
ключ Sw2 разомкнут и левая обкладка конденсатора 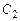 является плавающей, то заряд конденсатора
является плавающей, то заряд конденсатора 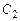 величины
величины 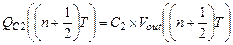 сохраняется до момента
сохраняется до момента 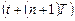 . По этой причине промежуток времени от
. По этой причине промежуток времени от 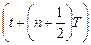 до
до 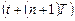 называется временем хранения, и выражение (1.47а) можно дополнить:
называется временем хранения, и выражение (1.47а) можно дополнить:
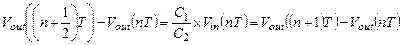 (1.47b)
(1.47b)
1.6. Реализация биквада на базе переключаемых конденсаторах
прямой заменой резисторов на переключаемые конденсаторы
Предположим, что резисторы имитируются переключаемым конденсатором (ПК) с частотой переключения 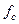 , много большей наивысшей частоты
, много большей наивысшей частоты 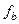 сигнала на входе фильтра. В этом случае номинал
сигнала на входе фильтра. В этом случае номинал 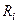 резистора в ARC реализации (в первом приближении) заменяется на эффективное сопротивление, определяемое выражением
резистора в ARC реализации (в первом приближении) заменяется на эффективное сопротивление, определяемое выражением
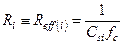 , (1.48)
, (1.48)
где номинал 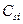 соответствующего переключаемого конденсатора определяется из этого же выражения (1.38). Одной из трудностей классической ARC реализации биквада является необходимость наличия в составе биквада отрицательного резистора. При использовании ОУ с недифференциальными выходами требуется введение в состав биквада дополнительного активного инвертора сигнала (пример активного инвертора – инвертирующий усилитель на рисунке 1.4 с одинаковыми резисторами
соответствующего переключаемого конденсатора определяется из этого же выражения (1.38). Одной из трудностей классической ARC реализации биквада является необходимость наличия в составе биквада отрицательного резистора. При использовании ОУ с недифференциальными выходами требуется введение в состав биквада дополнительного активного инвертора сигнала (пример активного инвертора – инвертирующий усилитель на рисунке 1.4 с одинаковыми резисторами 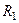 и
и  ). Красивым решением является использование полностью дифференциальных операционных усилителей (см. рис. 1.9), и, хотя такое решение удваивает количество пассивных компонентов, оно применяется практически везде, где нужны фильтры на базе ПК, по причине радикального снижения чувствительности к помехам и увеличения быстродействия.
). Красивым решением является использование полностью дифференциальных операционных усилителей (см. рис. 1.9), и, хотя такое решение удваивает количество пассивных компонентов, оно применяется практически везде, где нужны фильтры на базе ПК, по причине радикального снижения чувствительности к помехам и увеличения быстродействия.
При проектировании биквада на базе переключаемых конденсаторов с ОУ, имеюших недифференциальные выходы, применение инверторов сигналя принципиально НЕ является необходимым, поскольку существует инвертор заряда, описанный выше как инвертирующий переключаемый конденсатор. Схема биквада на базе ОУ с недифференциальным выходом после прямой замены резисторов на ПК (включая неинвертирующие ПК и один инвертирующий), приведена на рис. 1.14.
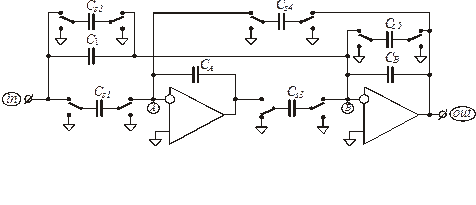
Рис. 1.15. Реализация биквада при прямой замене резисторов на ПК.
Отметим, что у некоторых переключаемых конденсаторов, например, CS1 и СS2, левые обкладки имеют одинаковый потенциал в любом из положений ключей, что позволяет объединить эти обкладки и подключать к соответствующим узлам с помощью единственного ключа. Одинаковый потенциал имеют также правая обкладка CS1 и левая обкладка CS4, правые обкладки CS2 и CS3 и левая обкладка CS5, правые обкладки CS4 и CS5. Благодаря этому обстоятельству, схему можно упростить (оптимизировать). Оптимизированный вариант биквада на базе ПК представлен на рис. 1.15.
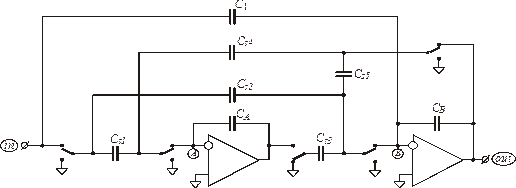
Рис. 1.16. Оптимизированная реализация биквада на рис. 1.15 на базе ОУ с одним выходом после объединения узлов с одинаковыми потенциалами.
Оптимизированная реализация полностью дифференциального ПК биквада представлена на рис. 1.17.
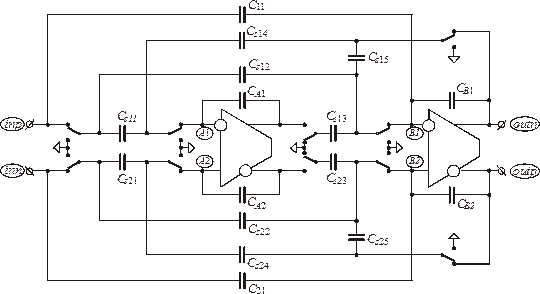
Рис. 1.17. Оптимизированная реализация полностью дифференциального ПК биквада
1.7. Дискретизация аналогового сигнала. Идеальные выборки
и z-преобразование.
Пример реализации биквада с использованием концепции переключаемых конденсаторов (ПК) демонстрирует лишь некоторые потенциальные достоинства этой концепции, а, именно, (А) упрощение технологии изготовления, неизмеримо более высокая точность характеристик фильтра в сравнении с ARC – реализацией и (В) возможность реализации «отрицательного резистора». Принцип переключаемых конденсаторов нашел применение не только в составе фильтров, но, даже в большей степени, – в цифроаналоговых и аналого-цифровых преобразователях и других субсистемах дискретно-аналоговой обработки сигнала, являющихся одними из главных субсистем любой цифровой системы связи. В связи с широчайшим использованием принципа ПК, существует необходимость обозначить достаточно «плавный» переход от классического преобразования Лапласа, как метода анализа схем непрерывного времени, к методу анализа аналоговых схем дискретного времени
Рассмотрим схему, дискретизирующую аналоговый сигнал, на рис.1.18.
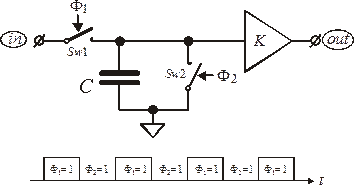
Рис. 1.18. Схема дискретизации аналогового сигнала.
Ключ 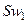 , замыкаясь в моменты времени Т, 2Т, 3Т, …, моментально заряжает конденсатор
, замыкаясь в моменты времени Т, 2Т, 3Т, …, моментально заряжает конденсатор 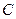 до мгновенного значения входного сигнала
до мгновенного значения входного сигнала 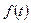 в эти же моменты Т, 2Т, 3Т, … и через бесконечно короткое время размыкается. На конденсаторе запоминаются мгновенные значения входного сигнала
в эти же моменты Т, 2Т, 3Т, … и через бесконечно короткое время размыкается. На конденсаторе запоминаются мгновенные значения входного сигнала 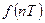 . Эти значения сигнала держится в течение времени
. Эти значения сигнала держится в течение времени 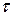 , и затем ключ
, и затем ключ 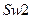 мгновенно разряжает конденсатор до нуля. На выходе дискретизатора находится буфер с коэффициентом усиления
мгновенно разряжает конденсатор до нуля. На выходе дискретизатора находится буфер с коэффициентом усиления 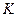 .
.
Дискретизированный эквивалент непрерывного входного сигнала изображен на рис. 1.19.
Определим ступенчатую функцию 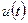 . Пусть
. Пусть 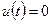 при
при 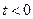 и
и 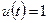 при
при 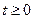 . Тогда n – й отсчет
. Тогда n – й отсчет 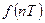 функции
функции 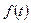 можно представить в виде:
можно представить в виде:
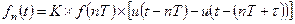 (1.49)
(1.49)
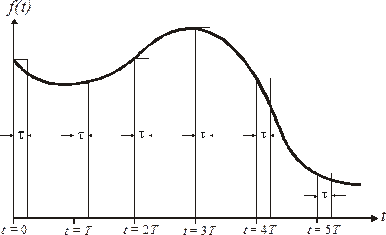
Рис. 1.19. Дискретизированный эквивалент непрерывного входного сигнала 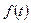 .
.
Определим ступенчатую функцию 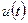 . Пусть
. Пусть 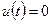 при
при 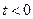 и
и 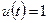 при
при 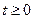 . Тогда n – й отсчет
. Тогда n – й отсчет 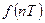 функции
функции 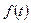 можно представить в виде:
можно представить в виде:
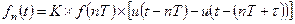 (1.50)
(1.50)
Предполагая 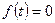 при
при 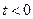 , дискретизированный эквивалент
, дискретизированный эквивалент 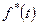 этой функции можно записать:
этой функции можно записать:
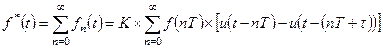 (1.51)
(1.51)
Произведем для дискретизированного сигнала 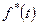 преобразование Лапласа и найдем его изображение
преобразование Лапласа и найдем его изображение 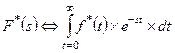 . Учитывая что
. Учитывая что 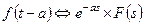 , а также
, а также 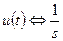 , получаем:
, получаем:
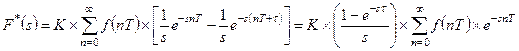 (1.52)
(1.52)
Пусть ширины 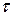 импульсов, представляющих функцию
импульсов, представляющих функцию 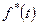 , очень малы, тогда в (1.44) можно записать:
, очень малы, тогда в (1.44) можно записать:
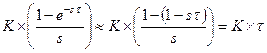 (1.53)
(1.53)
В выражении для 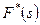 положим
положим 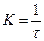 , т.е. пусть не амплитуда, а площадь каждого импульса функции
, т.е. пусть не амплитуда, а площадь каждого импульса функции 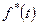 равна
равна 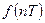 , и выражение (1.50) запишется в виде:
, и выражение (1.50) запишется в виде:
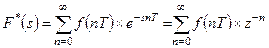 (1.54)
(1.54)
где 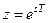 . Выражение (1.52) называется
. Выражение (1.52) называется 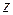 – преобразованием дискретных выборок
– преобразованием дискретных выборок 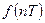 функции
функции 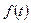 .
.
Из выражения (1.52) следует правило, чрезвычайно часто используемое в дискретных во времени системах, как цифровых, так и аналоговых: каждая выборка в z-области, задержанная на период сигнала дискретизации, отличается от не задержанной на множитель 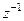 .
.
Поскольку z-преобразование является таким же интегральным преобразованием, как и преобразование Лапласа, все свойства 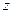 -преобразования практически повторяют свойства преобразования Лапласа, но с учетом (1.46), т.е.
-преобразования практически повторяют свойства преобразования Лапласа, но с учетом (1.46), т.е. 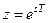 . В настоящем пособии z-преобразование использовано для определения передаточных функций дискретных во времени ПК интеграторов, как без задержки (на рис. 1.12), так и с задержкой (на рис. 1.14).
. В настоящем пособии z-преобразование использовано для определения передаточных функций дискретных во времени ПК интеграторов, как без задержки (на рис. 1.12), так и с задержкой (на рис. 1.14).
Дата добавления: 2022-02-05; просмотров: 388;











