Методы вычисления определенного интеграла

Численное решение рассматриваемой задачи в режиме программирования может быть выполнено следующими методами: метод прямоугольников, метод трапеций и метод Симпсона (метод парабол) и т. д. Эти методы с точки зрения программной реализации отличаются только способом вычисления площади фигуры, ограниченной отрезками функции в точках нижнего и верхнего пределов интегрирования [a, b], линией графика функции и отрезком оси X в границах [a, b]. Методы могут отличаться точностью результатов вычислений, если задачу решать без достижения требуемой точности, а также скоростью решения. Однако, если задачу решать, добиваясь требуемой точности результата, то указанные различия могут быть только в скорости решения. Различия в скорости решения можно определить по величине числа N, которое зависит от количества повторений (итераций) внешнего цикла в алгоритме задачи. Поэтому остановимся только на методе прямоугольников как наиболее простом.

Пример вычисления определенного интеграла :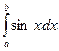

методом левых прямоугольников:

PROGRAM PRIMLP;

VAR A,B,N: INTEGER;

H, S, St : REL;

BEGIN

WRITELN (‘Введите A, B, N’);

READLN (A, B, N);

H: = (B-A)/N;

S: = 0;

X: = A;

FOR I: = 1 TO N DO BEGIN

St: =SIN(X)*H

S: = S + St;

X: = X + H;

END;

WRITELN (‘Значение интеграла =’, S:10:5);

END.

Просуммировав все найденные площади St, мы получим значение искомого интервала с некоторой погрешностью, которую можно уменьшить, увеличив число разбиений n.

Таблица 2 – Варианты заданий к УСРС

№ п/п	Функция f(x)	a	b		№ п/п	Функция f(x)	a	b
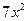
						5cos(x)	0,5
	2cos(x)		3p/2			2sin(x)	-p/2	p/2
	3sin(x)		p/2			3x3
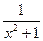
		0,5	1,5		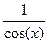			p/3
	2sin(x)+1					3x2
	6x2					3sin(x)	0,5	1,5
	(1+x)sin(x)					6x	0,5	1,5
	6cos(x)					5cos(x)
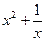
		0,5				2sin(x)
	cos(1 + x)		1,5			x2+cos(x)
	sin2(x)					8x2
	9x2					6cos(x)
	4cos(x)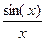
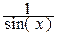
						4x3
	8x2					sin(x)+x

Форма контроля: представить преподавателю отчет в письменном виде по изученному разделу.

В отчет по работе следует включить цель работы, алгоритмы и программы вычисления определенного интеграла заданными численными методами. Все результаты вычисления интеграла свести в таблицу 3.

Таблица 3 – Результаты вычисления определенного интеграла

ЛИТЕРАТУРА

1. Аляев, Ю.А. Практикум по алгоритмизации и программированию на языке Паскаль: учеб. пособие / Ю.А. Аляев, В.П. Гладков, О.А. Козлов. – Москва : Финансы и статистика, 2004.

2. Вычислительная техника и информатика : метод. указания / сост. М.А. Прищепов, Н.В. Исаеня, Е.В. Севернева, Н.М. Жалобкевич. – Минск : БГАТУ, 2007.

3. Интегрированная среда программирования Turbo-Pascal : метод. указания / сост. М.А. Прищепов, Е.В. Севернева, А.И. Шакирин, Н.М.Жалобкевич. – Минск : БГАТУ, 2002.

4. Основы алгоритмизации и программирования на языке Turbo-Pascal : метод. указания / сост. М.А. Прищепов, Е.В. Севернева, А.И. Шакирин, Н.М.Жалобкевич. – Минск : БГАТУ, 2004.

5. Прищепов, М.А. Программирование на языках Basic, Pascal и Object Pascal в среде Delphi : учеб. пособие / М.А. Прищепов, Е.В. Севернева, А.И. Шакирин. – Минск : Тетра Системс, 2006. –318 с.

6. Прищепов, М.А. Экзамен по информатике. Основы алгоритмизации и программирования : учеб. пособие / М.А. Прищепов, Е.В. Севернева, В.П. Степанцов. – Минск : Тетра Системс, 2001. –312с.

7. Турчак, Л.И. Основы численных методов : учеб. пособие / Л.И. Турчак, П.В. Плотников. - Москва : ФизМат-лит.