Перечень основ термодинамики
Первое начало термодинамики – это закон сохранения и превращения энергии, которым сопровождаются термодинамические процессы. Оно утверждает: «Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме механических эквивалентов всех внешних воздействий».
Математически первое начало термодинамики можно записать так:
dU = dQ – dA + dM,
где dU – изменение внутренней энергии системы;
dQ – элементарное количество тепла, подводимого к системе;
dA – элементарная работа, совершаемая системой;
dM – другие виды элементарных энергий.
Если dM = 0, то
dU = dQ – dA или dQ = dU + dA.
Изотермический процесс – процесс, протекающий при постоянной температуре (T = const).
Первое начало термодинамики для изотермического процесса:таккак
dU = CVdT = 0, то U = const, а dQ = dU + dA = dA,
т.е. все подводимое к системе тепло идет на совершение этой системой работы.
Работа, совершаемая идеальным газом при изотермическом процессе:
а) для моля или киломоля идеального газа:
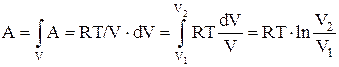 ,
,
или
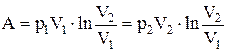 ;
;
б) для произвольной массы газа:
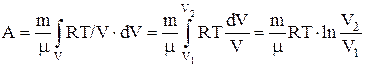 ,
,
или
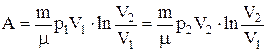 .
.
Изобарический процесс – процесс, протекающий при постоянном давлении (p = const).
Первое начало термодинамики для изобарического процесса:
dQp = dU + dA,
т.е. подводимое к системе тепло идет как на изменение ее внутренней энергии, так и на совершение этой системой работы. При этом:
а) для моля или киломоля идеального газа:
dQp = CpdT, dU = CVdT, dA = pdV = RdT;
б) для произвольной массы газа:
dQp = mCpdT/μ, dU = mCVdT/μ, dA = mpdV/μ = mRdT/μ.
Доля подводимой к системе энергии, которая идет на совершение работы:
dA = R/Cp×dQp = (1 – 1/g) dQp = dQp×(g – 1)/g.
Доля подводимой к системе энергии, которая идет на изменение внутренней энергии системы:
а) для моля или киломоля идеального газа:
dU = CVdT = dQp CV/Cp = dQp/g;
б) для произвольной массы газа:
dU = mCV×dT/μ = m×dQpCV/μCp = mdQp/μg,
где g = Cp/CV.
Изохорический процесс – процесс, протекающий при постоянном объеме (V = const).
Первое начало термодинамики для изохорического процесса:
Так как dA = p×dV = 0,
то dQV = dU + dA = dU,
т.е. при изохорическом процессе все подводимое к системе тепло идет на изменение ее внутренней энергии. При этом
dQV = CVdT,
следовательно,
dU = CVdT, или DU = CvDT.
Изменение внутренней энергии системы пропорционально изменению ее температуры.
Адиабатические или адиабатные процессы –процессы, протекающие без теплообмена или почти без теплообмена с окружающей средой. Примером адиабатического процесса может служить быстро протекающий процесс сжатия или расширения газа.
Первое начало термодинамики для адиабатического процесса: так как dQ = 0, то
dU + dA = 0, a dA = –dU,
т.е. работа, совершаемая системой при адиабатическом процессе, сопровождается уменьшением ее внутренней энергии.
Связь между параметрами состояния системы при адиатическом процессе (уравнения Пуассона):
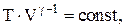
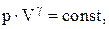
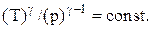
Работа, совершаемая произвольной массой m идеального газа при адиабатическом расширении:
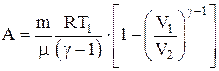 .
.
Политропическим называют процесс, при котором p и V связаны следующими соотношениями:
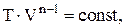
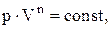
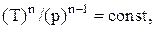
где n – показатель политропы, принимающий любые значения от –¥ до +¥.
Работа, совершаемая идеальным газом при политропическом процессе:
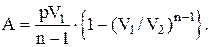
Обратимый процесс– это процесс, который протекает так, что после его окончания систему можно вернуть в первоначальное состояние, причем никаких изменений в окружающей систему среде не произойдет.
Необратимый процесс– это процесс, протекающий так, что после его окончания систему нельзя вернуть в первоначальное состояние без изменений в окружающей среде.
Круговой процесс (цикл) – это такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, возвращается в него вновь.
Любой круговой процесс состоит из процессов расширения и сжатия. Процесс расширения сопровождается работой, совершаемой системой, а процесс сжатия – работой, совершаемой над системой внешними силами. Разность этих работ равна работе данного цикла.
Если работа при расширении больше, чем работа при сжатии, то такой процесс (цикл) называется прямым. В противном случае – обратным.
Коэффициент полезного действия при круговых процессах (характеристика эффективности цикла) – физическая величина, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе:
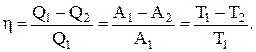
Цикл Карно состоит из двух изотермических и двух адиабатических процессов.
Коэффициент полезного действия цикла Карно (КПД)
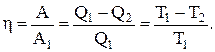
КПД цикла Карно не зависит от природы вещества, а зависит лишь от температур, при которых теплота сообщается системе и отбирается от нее.
Коэффициент полезного действия холодильной машины (холодильника)
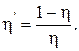
Примечание. Кроме цикла Карно в технической термодинамике применяются цикл Отто, состоящий из двух адиабатических и двух изохорических процессов, и цикл Дизеля, состоящий из двух адиабатических, изохорического и изобарического процессов.
Энтропия – физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс:
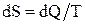 .
.
Связь энтропии системы с термодинамической вероятностью (соотношение Больцмана):
S = k×lnw,
где k – постоянная Больцмана.
Изменение энтропии системы при переходе из одного состояния в другое:
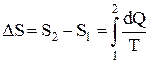 ,
,
или
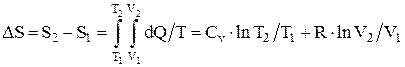 .
.
Изменение энтропии системы при изотермическом процессе:
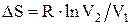 .
.
Изменение энтропии системы при изобарическом процессе:
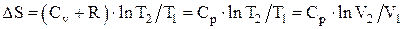 .
.
Изменение энтропии системы при изохорическом процессе:
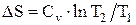 .
.
Изменение энтропии системы при адиабатическом процессе:
DS = 0, 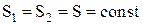 .
.
Изменение энтропии системы, совершающей цикл Карно:
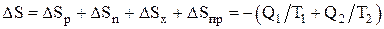 ,
,
где DSр – изменение энтропии рабочего тела;
DSн, DSх – изменение энтропии нагревателя и холодильника;
DSпр – изменение энтропии «потребителя работы».
В случае совершения системой обратимого цикла Карно энтропия замкнутой системы не изменяется:
DSобр = 0, или Sобр = const.
В случае совершения системой необратимого цикла Карно энтропия замкнутой системы возрастает:
DS > 0; 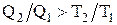 ;
; 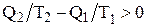 .
.
Для произвольных процессов, происходящих в замкнутой системе, энтропия системы для любых, происходящих в ней процессах, не может убывать:
DS ³ 0 или 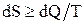 ,
,
где знак «равенства» справедлив для обратимых процессов, а знак «неравенства» – для необратимых.
Второе начало термодинамики: «В изолированной системе возможны только такие процессы, при которых энтропия системы возрастает или невозможен процесс, единственным результатом которого является превращение в работу теплоты, полученной от нагревателя»:
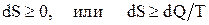 .
.
Термодинамические потенциалы – определенные функции объема V, давления p, температуры T, энтропии S, числа частиц системы N и других макроскопических параметров x, характеризующих состояние термодинамической системы:
а) внутренняя энергия – энергия системы, зависящая от ее внутреннего состояния. Она является однозначной функцией независимых переменных, определяющих это состояние, например температуры T и объема V (или давления p):
U = U (S, V, N, x).
Изменение внутренней энергии системы DU определяется лишь ее значениями в начальном и конечном состояниях:
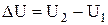 ;
;
б) энтальпия (теплосодержание) характеризует состояние макроскопической системы в термодинамическом равновесии при выборе в качестве основных независимых переменных энтропии S и давления p:
H = H (S, p, N, x).
Энтальпия системы равна сумме энтальпий составляющих ее частей.
Связь энтальпии с внутренней энергией U системы:
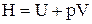 ,
,
где V – объем системы.
Полный дифференциал энтальпии (при неизменных N и x) имеет вид
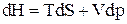 .
.
Связь энтальпии с температурой, объемом и теплоемкостью (при постоянном давлении) системы:
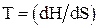 ;
; 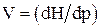 ; Cp = (dH/dt).
; Cp = (dH/dt).
Изменение энтальпии (DH) равно количеству теплоты, которое сообщают системе или отводят от нее при постоянном давлении, поэтому значения H характеризуют тепловые эффекты фазовых переходов (плавления, кипения и т. д.), химических реакций и других процессов, протекающих при постоянном давлении;
в) свободная энергия – одно из названий изохорно-изотермического термодинамического потенциала или Гельмгольца энергии. Представляет собой ту часть внутренней энергии системы, которая превращается во внешнюю работу при обратимых изотермических процессах F = F(V, T, N, x):
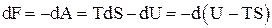 ,
,
где TS – связанная энергия.
Связанная энергия представляет собой ту часть внутренней энергии, которая не может быть передана в виде работы при изотермическом процессе:
TS = U – F.
Изменение (уменьшение) свободной энергии при необратимых изотермических процессах определяет наибольшую величину работы, которую может совершить система:
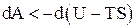 ;
; 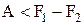 ;
;
г) энергия Гиббса – изобарно-изотермический потенциал, свободная энтальпия, характеристическая функция термодинамической системы при независимых параметрах p, T и N – G. В изотермически равновесном процессе, при постоянном давлении, убыль энергии Гиббса системы равна полной работе системы за вычетом работы против внешнего давления (т.е. равна максимальному значению «полезной» работы):
G = G (p, T, N, x); 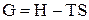 .
.
Связь энергии Гиббса со свободной энергией:
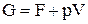 ;
;
д) химический потенциал – физическая величина, равная энергии Гиббса отдельно взятой частицы.
Третье начало термодинамики (теорема Нернста): «Изменение энтропии системы (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю. При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю»:
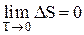 .
.
Термодинамика неравновесных процессов – общая теория макроскопического описания неравновесных процессов. Основная задача термодинамики неравновесных процессов – количественное изучение этих процессов для состояний, не сильно отличающихся от равновесного состояния.
Закон сохранения массы:
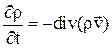 ,
,
где r – плотность многокомпонентной системы;
v – гидродинамическая скорость среды (средняя скорость переноса массы), зависящая от координат и времени;
rv – поток массы.
Закон сохранения массы для концентрации какого-либо компонента 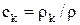 :
:
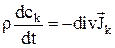 ,
,
где ck – концентрация компонента;
rk – плотность компонента;
r – плотность среды;
Jk = rk(vk – v) – диффузионный поток;
vk – гидродинамическая скорость (средняя скорость переноса массы) компонента.
Закон сохранения импульса:изменение импульса элементарного объема может происходить за счет сил, вызванных градиентом внутренних напряжений в среде Pa,b, и внешних сил Fk.
Закон сохранения энергии представляет собой первое начало термодинамики в термодинамике неравновесных процессов.
Уравнение баланса энтропии: «В термодинамике неравновесных процессов принимается, что энтропия элементарного объема является такой же функцией от внутренней энергии, удельного объема и концентрации, как и в состоянии полного равновесия»:
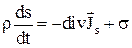 ,
,
где s – скорость возрастания энтропии;
r – плотность вещества;
s – энтропия элементарного объема (локальная энтропия);
Js – плотность потока энтропии.
Дата добавления: 2022-02-05; просмотров: 391;











