Основные положения и законы термодинамики
1. Первое начало термодинамики гласит: «Изменение внутренней энергии системы при переходе из одного состояния в другое равно сумме механических эквивалентов всех внешних воздействий». Математически это можно записать так: 
 , где dU – изменение внутренней энергии системы; dQ – элементарное количество тепла, подводимого к системе; dA – элементарная работа, совершаемая системой; dM – другие виды элементарных энергий. Можно ли утверждать, что оно является:
, где dU – изменение внутренней энергии системы; dQ – элементарное количество тепла, подводимого к системе; dA – элементарная работа, совершаемая системой; dM – другие виды элементарных энергий. Можно ли утверждать, что оно является:
а) законом сохранения и превращения энергии, которым сопровождаются термодинамические процессы;
б) утверждением, согласно которому термодинамическая система может совершать работу только за счёт своей внутренней энергии;
в) утверждением, согласно которому термодинамическая система может совершать работу не только за счёт каких-либо внешних источников энергии;
г) утверждением о невозможности существования вечных двигателей первого рода, который совершал бы работу, не потребляя энергию из какого-либо внешнего источника.
2. Соотношение, которое полностью отображает первое начало термодинамики:
а) 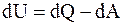 ;
;
б) 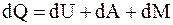 ;
;
в)  ;
;
г) 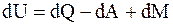 .
.
3. Первое начало термодинамики утверждает, что:
а) каждое состояние термодинамической системы характеризуется определённым значением внутренней энергии U, независимо от того, каким путём система приведена в данное состояние;
б) внутренняя энергия термодинамической системы U является функцией состояния системы;
в) каждое состояние термодинамической системы характеризуется определённым значением внутренней энергии U, в зависимости от того, каким путём система приведена в данное состояние.
4. Первое начало термодинамики утверждает, что:
а) работа, совершаемая термодинамической системой, зависит от процесса, приведшего к изменению состояния системы;
б) количество тепла, сообщенное термодинамической системе, зависит от процесса, приведшего к изменению состояния системы;
в) работа, совершаемая термодинамической системой, является функцией состояния системы;
г) количество тепла, сообщенное термодинамической системе, является функцией состояния системы.
5. Формула, представляющая собой математическую запись первого начала термодинамики для произвольной массы газа:
а)  ;
;
б)  ;
;
в) 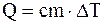 ;
;
г)  .
.
6. Изотермический процесс – процесс, протекающий при постоянной температуре (T = const). При изотермическом процессе:
а) внутренняя энергия системы изменяется;
б) внутренняя энергия системы остаётся величиной постоянной;
в) все подводимое к системе тепло идет на совершение этой системой работы;
г) часть подводимого к системе тепла идет на совершение этой системой работы.
7. Работа, совершаемая произвольной массой m идеального газа при изотермическом процессе, определяется соотношением:
а) 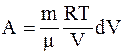 ;
;
б)  ;
;
в)  ;
;
г)  .
.
8. Изобарический процесс – процесс, протекающий при постоянном давлении (p = const). При этом подводимое к системе тепло идёт:
а) как на изменение ее внутренней энергии, так и на совершение этой системой работы;
б) только на изменение ее внутренней энергии;
в) только на совершение этой системой работы.
9. Работа, совершаемая произвольной массой m идеального газа при изобарическом процессе, определяется соотношением:
а)  ;
;
б) 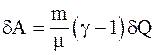 ;
;
в) 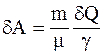 ;
;
г)  .
.
10. Изменение внутренней энергии произвольной массы m идеального газа при изобарическом процессе определяется соотношением:
а) 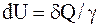 ;
;
б)  ;
;
в)  .
.
11. Если температура идеального газа увеличилась в 4 раза, то его внутренняя энергия увеличилась в:
а) 4 раза;
б) 2 раза;
в) 1,5 раза;
г) 2,5 раза;
д) не изменилась.
12. Изохорический процесс – это процесс, протекающий при постоянном объеме (V = const). При этом все подводимое к системе тепло идет на изменение ее внутренней энергии. Какие из приведенных соотношений справедливы в данном случае?
а) 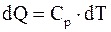 ;
;
б)  ;
;
в) 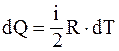 ;
;
г) 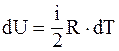 .
.
13. Адиабатический процесс – это процесс, протекающий без теплообмена или почти без теплообмена с окружающей средой. При этом работа:
а) может совершаться системой только за счет убыли её внутренней энергии;
б) может совершаться системой только за счет возрастания её внутренней энергии;
в) может совершаться системой только за счет энергии из других внешних источников.
14. Какие из приведенных соотношений справедливы для адиабатического процесса (являются уравнениями Пуассона)?
а) 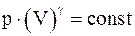 ;
;
б)  ;
;
в)  ;
;
г)  .
.
15. Работа, совершаемая произвольной массой m идеального газа при адиабатическом расширении, определяется по формуле:
а) 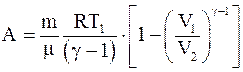 ;
;
б) 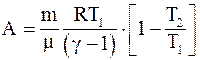 ;
;
в) 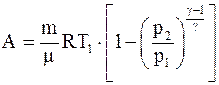 .
.
16. Если ΔU – изменение внутренней энергии идеального газа, А – работа газа, Q – количество теплоты, сообщаемое газу, то для адиабатного расширения газа справедливы следующие соотношения:
а) Q > 0; A > 0; ΔU = 0;
б) Q = 0; A > 0; ΔU < 0;
в) Q < 0; A < 0; ΔU = 0;
г) Q = 0; А < 0; ΔU > 0.
17. Если над термодинамической системой внешними силами совершается работа A и той же системе передаётся некоторое количество теплоты Q, то этом случае изменение внутренней энергии DU системы будет равно:
а) DU = A;
б) DU = Q;
в) DU = A + Q;
г) DU = A – Q.
18. Какие из приведенных соотношений справедливы для политропического процесса?
а) 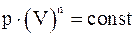 ;
;
б)  ;
;
в)  ;
;
г) 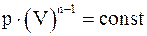 .
.
19. Работа, совершаемая произвольной массой m идеального газа при политропическом процессе:
а)  ;
;
б) 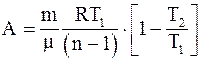 ;
;
в) 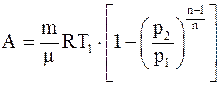 .
.
20. Если переданное идеальному газу количество теплоты в любой момент времени равно работе, совершённой газом, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
21. Если переданное идеальному газу количество теплоты в любой момент времени равно изменению внутренней энергии газа, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
22. Если в любой момент времени совершенная идеальным газом работа равна изменению внутренней энергии термодинамической системе, то можно утверждать, что в данном газе совершается:
а) адиабатический процесс;
б) изотермический процесс;
в) изобарический процесс;
г) изохорический процесс.
23. Внутренняя энергия тела может изменяться:
а) только при передаче телу некоторого количества теплоты;
б) только при совершении внешними силами над телом механической работы;
в) при изменении кинетической и потенциальной энергии тела как целого;
г) при передаче телу теплоты и при совершении над ним работы.
24. При изобарическом процессе работа газа всегда:
а) равна нулю;
б) положительна;
в) отрицательна;
г) зависит от величины давления и от изменения объема.
25. Работа, совершаемая идеальным газом при круговом процессе (цикле):
а) эквивалентна разности количеств тепла, подводимого к системе при расширении Q1 и отводимого от нее при сжатии Q2;
б) эквивалентна разности количеств тепла, отводимого от системы при сжатии Q2 и подводимого к системе при расширении Q1;
в) равна разности работ при расширении А1 и при сжатии А2 газа;
г) равна разности работ при при сжатии А2 и расширении А1 газа.
26. Коэффициент полезного действия кругового процесса (цикла) – это:
а) физическая величина, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе;
б) физическая величина, равная отношению разности количества тепла, подведенного к системе, и количества тепла, отданного системой, к количеству тепла, отданного системой;
в) физическая величина, равная отношению разности количества тепла, подведенного к системе, и количества тепла, отданного системой, к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе.
27. Цикл Карно – это:
а) цикл, состоящий из последовательно чередующихся двух изотермических и двух адиабатических процессов, осуществляемых с рабочим телом (например, паром);
б) цикл, состоящий из последовательно чередующихся двух адиабатических и двух изотермических процессов, осуществляемых с рабочим телом (например, паром);
в) обратимый круговой процесс, в котором совершается превращение теплоты в работу (или работы в теплоту);
г) необратимый круговой процесс, в котором совершается превращение теплоты в работу (или работы в теплоту).
28. Тепловая машина работает по циклу Карно. Если температуру нагревателя увеличить, то КПД цикла:
а) не изменится;
б) увеличится;
в) уменьшится.
29. На рисунке 1 изображен цикл Карно в координатах (T,S), где S – энтропия. Изотермическое расширение происходит на этапе:
| а) 3 – 4; б) 1 – 2; в) 4 – 1; г) 2 – 3. | 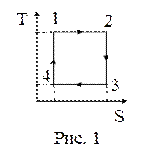
|
30. Математически первое начало термодинамики для изотермического процесса можно отобразить следующими соотношениями:
а) T = const; PV = const; U = const;
б) T = const; PV/R = const; U = 0;
в) PV = const; Q = DU; Aг = 0;
г) T = const; Q = Aг; DU = 0.
31. Работа, совершаемая произвольной массой m идеального газа цикл Карно, определяется соотношением:
а)  ;
;
б) 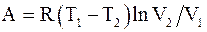 ;
;
в) 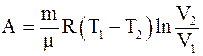 .
.
32. На рисунке 1 в координатах p – V представлен цикл Карно. На участке АВ рабочее тело приводится в соприкосновение с нагревателем, находящимся при температуре T1, и:
| а) расширяясь, совершает работу; б) только расширяется; в) только совершает работу; г) изотермически получает от нагревателя некоторое количество тепла. | 
|
33. На рисунке 1 в координатах p – V представлен цикл Карно. На участке ВС рабочее тело:
| а) расширяясь адиабатически, совершает работу; б) только расширяется; в) только совершает работу; г) адиабатически охлаждается до температуры Т2. | 
|
34. На рисунке 1 в координатах p – V представлен цикл Карно. На участке СD рабочее тело:
| а) сжимаясь адиабатически, совершает работу; б) сжимаясь изотермически, совершает работу; в) сжимаясь изотермически, совершает работу; г) сжимаясь изотермически, отдаёт некоторое количество тепла. | 
|
35. На рисунке 1 в координатах p – V представлен цикл Карно. На участке АD рабочее тело:
| а) сжимаясь адиабатически, отдаёт холодильнику некоторое количество тепла; б) сжимаясь изотермически, совершает работу; в) сжимаясь изотермически, не совершает работу; г) сжимаясь изотермически, отдаёт холодильнику некоторое количество тепла. | 
|
36. На рисунке 1 в координатах p – V представлен цикл Карно. В точке В температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
37. На рисунке 1 в координатах p – V представлен цикл Карно. В точке C температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
38. На рисунке 1 в координатах p – V представлен цикл Карно. В точке D температура рабочего тела равна температуре точки:
| а) А; б) С; в) D. | 
|
39. На рисунке 1 в координатах p – V представлен цикл Карно. Работа данного цикла численно равна площади фигуры:
| а) АBMNA; б) DCLKD; в) ABСD; г) ADKNA. | 
|
40. Коэффициент полезного действия цикла Карно h:
а) не зависит от природы вещества;
б) зависит от природы вещества;
в) зависит лишь от температур, при которых теплота сообщается системе и отбирается от нее;
г) не зависит от температур, при которых совершаются последовательные изотермические и адиабатические процессы.
41. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия цикла Карно h определяется соотношением:
а)  ;
б) ;
б)  ; ;
| в)  ;
г) ;
г) 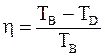 . .
| 
|
42. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия цикла Карно h численно равен отношению:
| а) площади фигуры ABCDA к площади фигуры ABMNA; б) площади фигуры ABCDA к площади фигуры CLKDC; в) разности площадей фигур ABMNA и CLKDC к площади фигуры ABMNA; г) разности площадей фигур ABMNA и CLKDC к площади фигуры CLKDC; д) среди приведенных ответов правильного ответа нет. | 
|
43. На рисунке 1 в координатах p – V представлен цикл Карно. Коэффициент полезного действия холодильной машины (холодильника)  определяется соотношением:
определяется соотношением:
а)  ;
б) ;
б)  ; ;
| в)  ;
г) ;
г) 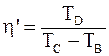 . .
| 
|
44. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Отто соответствует рисунок:
| а) 1; б) 2; в) 3. | 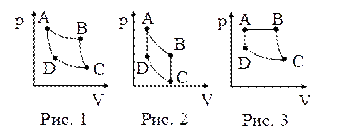
|
45. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Дизеля соответствует рисунок:
| а) 3; б) 2; в) 1. | 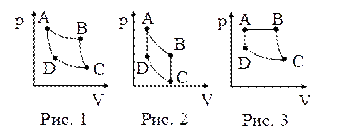
|
46. На рисунках 1–3 в координатах p – V представлены циклы Карно, Отто и Дизеля. Циклу Карно соответствует рисунок:
| а) 3; б) 2; в) 1. | 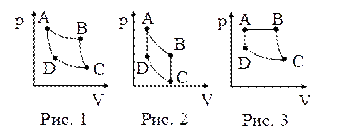
|
47. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, отдаёт холодильнику 500 Дж теплоты. В этом случае работа, совершаемая тепловой машиной, равна:
а) 1000 Дж
б) 750 Дж;
в) 500 Дж;
г) 250 Дж.
48. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, получает от нагревателя 500 Дж теплоты. В этом случае работа, совершаемая тепловой машиной, равна:
а) 1000 Дж
б) 750 Дж;
в) 500 Дж;
г) 250 Дж.
49. За один цикл тепловая машина, коэффициент полезного действия которой h = 50 %, совершает работу в 500 Дж. В этом случае тепловая машина отдаёт холодильнику:
а) 1000 Дж теплоты;
б) 750 Дж теплоты;
в) 500 Дж теплоты;
г) 250 Дж теплоты.
50. Газ совершает работу против внешних сил 500 Дж, получая из вне 500 Дж теплоты. В этом случае изменение внутренней энергии газа равно:
а) 0 Дж;
б) 300 Дж;
в) 200 Дж;
г) 100 Дж.
51. Если тепловая машина с КПД 50% за один цикл отдает холодильнику 500 Дж теплоты, то работа, совершаемая машиной за один цикл, равна:
а) 250 Дж;
б) 500 Дж;
в) 750 Дж;
г) 800 Дж.
52. Над термодинамической системой внешние силы совершают работу, равную A, и этой же системе передаётся количество тепла, равное Q. Изменение внутренней энергии термодинамической системы ∆U в этом случае равно:
а) 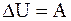 ;
;
б)  ;
;
в)  ;
;
г) 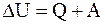 .
.
53. Абсолютная температура нагревателя в идеальной тепловой машине вдвое больше температуры холодильника, КПД такой машины равен:
а) 600 %;
б) 50 %;
в) 40 %;
г) 30 %.
54. Если температура нагревателя идеальной тепловой машины 227ºС, а температура холодильника 27ºС, то газ в машине совершает полезную работу, равную:
а) 0,4 Q;
б) 0,5 Q;
в) 0,6 Q;
г) 0,7 Q.
55. КПД идеальной тепловой машины, которая совершает полезную работу 200 Дж, получая для этого 800 Дж теплоты, равен:
а) 40 %;
б) 10 %;
в) 20 %;
г) 25 %.
56. Диаграмма циклического процесса идеального одноатомного газа представлена на рисунке 1. Отношение работы при нагревании газа к работе при охлаждении равно:
| а) 3; б) 5; в) 1,5; г) 2,5. | 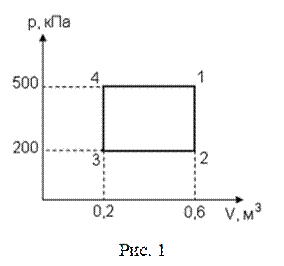
|
57. В идеальной тепловой машине абсолютная температура нагревателя вдвое больше температуры холодильника. Если, не меняя температуру нагревателя, температуру холодильника уменьшить вдвое, то КПД этой машины:
а) возрастет на 20 %;
б) возрастет на 25 %;
в) возрастет на 30 %;
г) возрастет на 35 %.
58. Энтропия – это:
а) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно только полученному количеству теплоты, деленному на температуру, при которой произошел этот процесс;
б) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно только отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс;
в) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно любому количеству теплоты, деленному на температуру, при которой произошел этот процесс;
г) физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс.
59. В термодинамике энтропия – это:
а) мера обратимого и необратимого рассеяния энергии;
б) мера обратимого рассеяния энергии;
в) мера необратимого рассеяния энергии;
г) функция состояния системы, которая позволяет строго математически сформулировать второе начало термодинамики.
60. Второе начало термодинамики:
а) «В изолированной системе возможны только такие процессы, при которых энтропия системы возрастает»;
б) «В изолированной системе возможны только такие процессы, при которых энтропия системы убывает»;
в) «В изолированной системе возможны только такие процессы, при которых энтропия системы остаётся величиной постоянной»;
г) «Невозможен процесс, единственным результатом которого является превращение в работу теплоты, полученной от нагревателя».
61. Математически второе начало термодинамики отображается соотношением:
а) 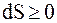 ;
;
б)  ;
;
в) 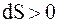 ;
;
г)  .
.
62. Связь энтропии системы с вероятностью выражается соотношением:
а)  ;
;
б) 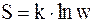 ;
;
в)  ;
;
г) 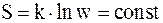 .
.
63. В общем случае изменение энтропии системы при переходе из одного состояния в другое определяется формулой:
а)  ;
;
б) 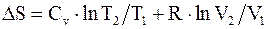 ;
;
в)  ;
;
г)  .
.
64. Изменение энтропии системы при изотермическом процессе:
а)  ;
;
б) 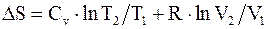 ;
;
в)  ;
;
г)  .
.
65. Изменение энтропии системы при изобарическом процессе:
а)  ;
;
б) 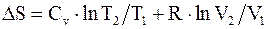 ;
;
в) 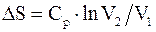 ;
;
г)  .
.
66. Изменение энтропии системы при изохорическом процессе:
а)  ;
;
б) 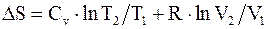 ;
;
в) 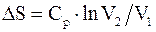 ;
;
г)  .
.
67. Изменение энтропии системы при адиабатическом процессе:
а)  ;
;
б) 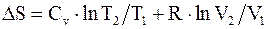 ;
;
в) 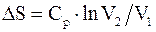 ;
;
г)  .
.
68. Изменение энтропии системы, совершающей цикл Карно:
а) 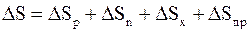 ;
;
б)  ;
;
в)  ;
;
г) 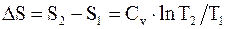 .
.
69. В случае совершения системой обратимого цикла Карно энтропия замкнутой системы:
а) изменяется;
б) не изменяется;
в) остаётся величиной постоянной;
г) уменьшается.
70. В случае совершения системой необратимого цикла Карно энтропия замкнутой системы:
а) возрастает;
б) не изменяется;
в) остаётся величиной постоянной;
г) уменьшается.
71. Для произвольных процессов, происходящих в замкнутой системе, энтропия системы:
а)  ;
;
б)  ;
;
в) 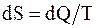 ;
;
г)  .
.
72. Для произвольных процессов, происходящих в замкнутой системе, энтропия:
а) может убывать;
б) не может убывать;
в) не может возрастать;
г) может возрастать.
73. Третье начало термодинамики (теорема Нернста) формулируется так:
а) «Изменение энтропии системы (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при любых температурах, стремится к нулю»;
б) «Изменение энтропии системы (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю»;
в) «При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю»;
г) «При помощи последовательности термодинамических процессов можно достичь температуры, равной абсолютному нулю».
74. Термодинамика неравновесных процессов – это:
а) общая теория макроскопического описания неравновесных процессов, позволяющая количественное изучение этих процессов для состояний, не сильно отличающихся от равновесного состояния;
б) общая теория макроскопического описания неравновесных процессов, позволяющая количественное изучение этих процессов для любых состояний;
в) общая теория макроскопического описания равновесных процессов;
г) общая теория макроскопического описания неравновесных процессов.
75. На рисунке 1 представлен цикл тепловой машины в координатах Т, S, где Т – термодинамическая температура, S – энтропия. Укажите нагреватели и холодильники с соответствующими температурами:
| а) нагреватели – Т3, Т5, холодильники – Т1, Т2, Т4; б) нагреватели – Т3, Т4, Т5, холодильники – T1 Т2; в) нагреватели – Т4, Т5, холодильники – T1, Т2, Т3; г) нагреватели – Т2 Т4, Т5, холодильники – T1, Т3; д) среди приведенных ответов правильного ответа нет. | 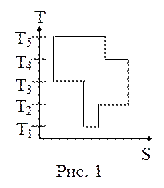
|
76. На рисунке 1 изображен цикл Карно в координатах (T,S), где S – энтропия. Изотермическое расширение происходит на этапе:
| а) 3-4; б) 1-2; в) 4-1; г) 2-3. | 
|
Дата добавления: 2022-02-05; просмотров: 600;











