Основы релятивистской механики

1. Принцип относительности Галилея (в классической механике) утверждает:

а) «Никакие опыты, проводимые в любых системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой отсчета»;

б) «Никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой произвольной системе отсчета»;

в) «Никакие опыты, проводимые в инерциальных системах отсчета с механическими приборами, не позволяют установить, покоится система отсчета или движется равномерно и прямолинейно по отношению к другой инерциальной системе отсчета».

Примечание. Предполагается, что время не зависит от относительного движения систем отсчета.

2. Преобразования Галилея определяют положение произвольной материальной точки в двух инерциальных системах отсчета, одна из которых движется со скоростью 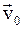относительно другой при условии:

а) если направление скорости 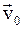не совпадает с направлением радиус-вектора 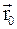, определяющим положение начала координат подвижной системы отсчёта К^' в неподвижной системе координат К;

б) если направление скорости 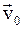совпадает с направлением радиус-вектора 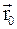, определяющим положение начала координат подвижной системы отсчёта К^' в неподвижной системе координат К;

в) если направление скорости 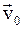совпадает с направлением радиус-вектора 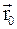, определяющим положение начала координат подвижной системы отсчёта К^'.

3. В векторной форме преобразования Галилея можно представить так:

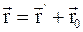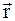а) , где и 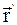– радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени; 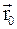– радиус-вектор, определяющий положение начала подвижной системы координат К^' в неподвижной системе координат К;

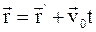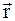б) , где и 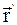– радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени; 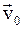– скорость движения подвижной системы координат;

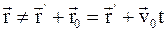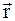в) , где и 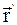– радиус-векторы, определяющие положение материальной точки в неподвижной и подвижной инерциальных системах отсчета в данный момент времени; 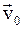– скорость движения подвижной системы координат.

4. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату x выбранной точки в неподвижной системе отсчета К можно определить так:

а) ;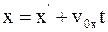

б) ;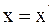

в) .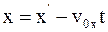

5. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату y выбранной точки в неподвижной системе отсчета К можно определить так:

а) ;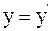

б) ;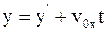

в) .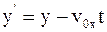

6. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату z выбранной точки в неподвижной системе отсчета К можно определить так:

а) ;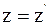

б) ;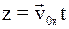

в) .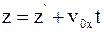

7. Преобразования Галилея справедливы в том случае, когда время в подвижной инерциальной системе отсчёта и неподвижной инерциальной системе отсчёта:

а) ;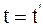

б) ;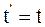

в) .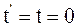

8. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату x' выбранной точки в подвижной системе отсчета К' можно определить так:

а) ;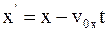

б) ;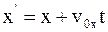

в) .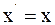

9. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату y' выбранной точки в подвижной системе отсчета К' можно определить так:

а) ;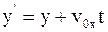

б) ;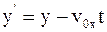

в) .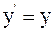

10. Используя преобразования Галилея в проекциях на оси координат в произвольный момент времени t, координату z' выбранной точки в подвижной системе отсчета К' можно определить так:

а) ;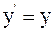

б) ;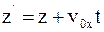

в) .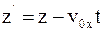

11. Ковариантные, или инвариантные, уравнения – это уравнения, обе части которых при переходе от одной системы координат к другой преобразуются:

а) одинаково и сохраняют свой вид во всех инерциальных системах отсчета;

б) неодинаково и несохраняют свой вид во всех инерциальных системах отсчета;

в) одинаково, но несохраняют свой вид во всех инерциальных системах отсчета.

12. Закон сложения скоростей в классической механике отображается соотношением:

а) ;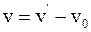

б) ;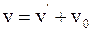

в) .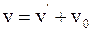

13. Теория относительности – это физическая теория, рассматривающая пространственно-временные закономерности, справедливые:

а) только для механических процессов;

б) только для оптических процессов;

в) для любых физических процессов.

14. Инвариантность (симметрия) законов физики – это неизменность законов физики, устанавливающих соотношение между величинами, характеризующими физическую систему или определяющими изменение этих величин:

а) в пространстве при преобразованиях;

б) со временем при преобразованиях;

в) в пространстве и со временем при преобразованиях.

15. Относительное расстояние между выбранными точками пространства в подвижных системах отсчета определяется соотношением:

а) ;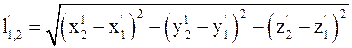

б) ;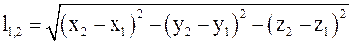

в) .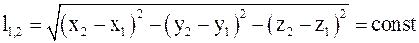

16. Относительное расстояние между выбранными точками пространства в неподвижных системах отсчета определяется соотношением:

а) ;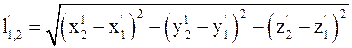

б) ;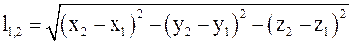

в) .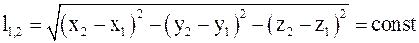

17. Инварианты преобразований – это инвариантные величины:

а) расстояния между телами (точками);

б) промежутки времени между событиями;

в) относительные скорости и ускорения тел.

18. Первый постулат специальной теории относительности (принцип относительности) утверждает:

а) «Механические и тепловые физические опыты, производимые внутри инерциальной системы отсчета, позволяют установить, находится ли она в равномерном абсолютном и прямолинейном движении или нет»;

б) «Никакие электромагнитные и оптические опыты, производимые внутри инерциальной системы отсчета, не позволяют установить, находится ли она в равномерном абсолютном и прямолинейном движении или нет»;

в) «Никакие физические опыты (механические, оптические, тепловые, электромагнитные и т.д.), производимые внутри инерциальной системы отсчета, не позволяют установить, находится ли она в равномерном абсолютном и прямолинейном движении или нет».

19. Второй постулат специальной теории относительности утверждает:

а) «Скорость света в вакууме одинакова во всех направлениях и не зависит от движения источника света»;

б) «Скорость света в вакууме одинакова во всех направлениях и зависит от движения источника света»;

в) «Скорость света в вакууме не зависит от движения источника света».

20. Третий постулат специальной теории относительности утверждает:

а) «События, одновременные в одной системе отсчета, являются одновременными в другой системе отсчета»;

б) «События, одновременные в одной системе отсчета, не являются одновременными в другой системе отсчета»;

в) «Одновременность событий является понятием относительным».

21. Формула преобразования координаты x в неподвижной системе координат, согласно преобразованиям Лоренца, имеет вид:

а) ;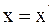

б) ;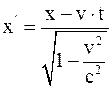

в) .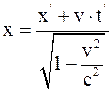

22. Формула преобразования координаты x' в подвижной системе координат, согласно преобразованиям Лоренца, имеет вид:

а) ;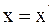

б) ;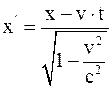

в) .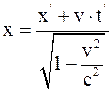

23. Формула преобразования времени в неподвижной системе координат, согласно преобразованиям Лоренца, имеет вид:

а) ;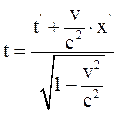

б) ;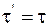

в) .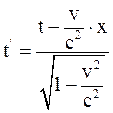

24. Формула преобразования времени в подвижной системе координат, согласно преобразованиям Лоренца, имеет вид:

а) ;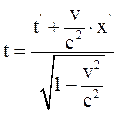

б) ;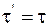

в) .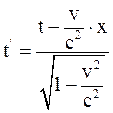

25. Если частица движется в неподвижной системе отсчёта вдоль оси x со скоростью v, то в момент времени t в подвижной системе отсчёта, движущейся относительно неподвижной со скоростью u, скорость частицы v', согласно преобразованиям Лоренца, определяется соотношением:

а) ;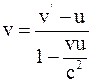

б) ;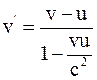

в) .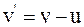

26. Часы, находящиеся в неподвижной системе отсчёта К в точке х = 0, показывают время t. В подвижной системе отсчёта К' часы, пространственно совпадающие с часами в неподвижной системе отсчёта К в этот момент времени, показывают время:

а) ;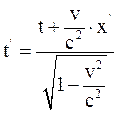

б) ;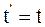

в) .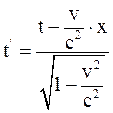

27. Соотношение, отображающее показания часами, находящимися в неподвижной системе отсчёта К в точке х = 0, и часами, находящимися в подвижной системе отсчёта К', пространственно совпадающими с часами в неподвижной системе отсчёта К, имеет вид:

а) ;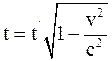

б) ;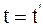

в) .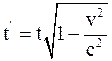

28. Длина стержня в подвижной инерциальной системе отсчёта (в направлении её скорости движения v) отображается соотношением:

а) ;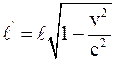

б) ;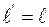

в) .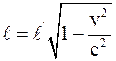

29. Размеры всех тел, покоящихся в неподвижной инерциальной системе отсчёта, при измерении в подвижной инерциальной системе отсчёта (в направлении её скорости движения v) оказываются:

а) равными ;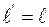

б) меньше в ;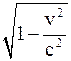

в) больше в .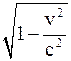

30. Продольный диаметр сферы, движущейся со скоростью v относительно неподвижной инерциальной системы отсчёта, при измерении в подвижной инерциальной системе отсчёта будет:

а) равен поперечному диаметру;

б) больше в 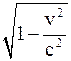раз поперечного диаметра;

в) меньше в 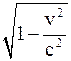раз поперечного диаметра.

31. Космический корабль с двумя космонавтами летит со скоростью v = 0,8c (с – скорость распространения света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, параллельного направлению движения, в положение 2, перпендикулярное этому направлению. Тогда длина стержня с точки зрения другого космонавта:

а) изменится от 1,0 м в положении 1 до 1,67 м в положении 2;

б) равна 1,0 м при любой его ориентации;

в) изменится от 1,0 м в положении 1 до 0,6 м в положении 2;

г) изменится от 0,6 м в положении 1 до 1,0 м в положении 2.

32. Импульс (вектор энергии – импульса) материальной точки в специальной теории относительности определяется соотношением:

а) ;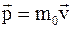

б) ;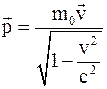

в) .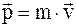

33. Уравнение движения материальной точки в специальной теории относительности можно записать так:

а) ;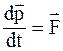

б) ;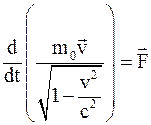

в) .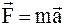

34. Кинетическая энергия тела в специальной теории относительности определяется соотношением:

а) ;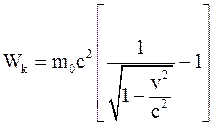

б) ;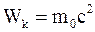

в) .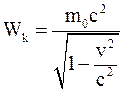

35. Между массой всякого физического объекта и присущей ему (во взаимосвязи с окружающей средой) полной энергией E имеет место соотношение:

а) ;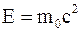

б) ;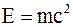

в) .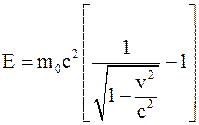

36. Всякое изменение энергии тела на величину DЕ влечет за собой изменение массы тела на Dm, причем:

а) ;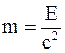

б) ;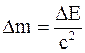

в) .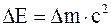

37. Закон взаимной связи энергии и массы утверждает: «Всякая материя (вещество в обычном смысле или излучение), обладающая энергией Е, обладает тем самым и массой m, равной:

а) »;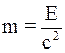

б) »;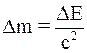

в) ».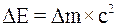

2. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ
И ТЕРМОДИНАМИКИ

2.1. Основные понятия молекулярной физики
и термодинамики

1. Молекулярная физика – раздел физики, в котором изучаются физические свойства и строение вещества в различных агрегатных состояниях на основе рассмотрения их:

а) микроскопического строения;

б) молекулярного строения;

в) микроскопического и молекулярного строения;

г) атомного строения.

2. Кинетическая теория газов позволяет исследовать:

а) смеси газов;

б) многоатомные газы, когда необходимо не учитывать внутренние степени свободы (колебательные и вращательные);

в) плотные газы, когда необходимо учитывать корреляции между сталкивающимися молекулами или многократные столкновения;

г) ионизованные газы (плазму), когда нельзя ограничиться учётом короткодействующих сил, а приходится также учитывать медленно убывающие с расстоянием кулоновские силы;

д) разряженные газы, когда длина свободного пробега частиц сравнима с размерами системы и необходимо учитывать столкновения частиц со стенками.

3. Статистическая физика – раздел молекулярной физики, в котором изучаются свойства макроскопических тел, т.е. систем, состоящих из очень большого числа одинаковых частиц, исходя из:

а) свойств этих частиц;

б) взаимодействий между частицами;

в) свойств этих частиц и взаимодействий между ними.

4. Термодинамика – раздел физики, в котором изучаются наиболее общие свойства макроскопических физических систем:

а) находящихся в состоянии термодинамического равновесия;

б) находящихся в состоянии термодинамического равновесия, и процессы перехода этих систем из одного состояния в другое состояние;

в) в связи с их микроскопическим строением.

5. Термодинамическая система – это:

а) совокупность молекул, атомов и частиц;

б) совокупность рассматриваемых тел;

в) совокупность рассматриваемых тел, в частности молекул, атомов, частиц.

6. Интенсивные параметры состояния системы – это:

а) параметры, зависящие от массы системы;

б) параметры, не зависящие от массы системы;

в) давление, температура и концентрация.

7. Температура – физическая величина:

а) которая определяет направление теплового обмена;

б) характеризующая состояние термодинамического равновесия макроскопической системы;

в) которая в молекулярной физике не определяет распределение частиц по уровням энергии;

г) которая в молекулярной физике определяет распределение частиц по скоростям.

8. Термодинамическая температурная шкала – температурная шкала:

а) определяемая температура (абсолютная температура) в которой всегда равна нулю;

б) определяемая температура (абсолютная температура) в которой всегда отрицательна;

в) определяемая температура (абсолютная температура) в которой всегда положительна.

9. Экстенсивные параметры термодинамической системы – это такие параметры её состояния:

а) значения которых пропорциональны массе термодинамической системы;

б) значения которых не зависят от массы термодинамической системы;

в) значения которых пропорциональны объёму термодинамической системы;

г) как объем, внутренняя энергия, энтропия.

10. Внутренняя энергия системы равна:

а) сумме кинетических энергий хаотического движения молекул, потенциальных энергий их взаимодействия и внутримолекулярной энергии;

б) энергии системы без учёта кинетической энергии её в целом (при движении) и потенциальной энергии во внешнем поле;

в) энергии системы с учётом кинетической энергии её в целом (при движении) и потенциальной энергии во внешнем поле.

11. Изменение внутренней энергии при переходе системы из состояния в состояние равно:

а) разности значений внутренней энергии в этих состояниях, которая не зависит от пути перехода системы из одного состояния в другое;

б) разности значений внутренней энергии в этих состояниях, которая зависит от пути перехода системы из одного состояния в другое;

в) сумме значений внутренней энергии в этих состояниях, которая не зависит от пути перехода системы из одного состояния в другое;

г) сумме значений внутренней энергии в этих состояниях, которая зависит от пути перехода системы из одного состояния в другое.

12. Основное уравнение состояния системы определяется соотношением:

а) ;

б) ;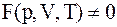

в) .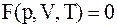

13. Неравновесное состояние системы – это такое её состояние, при котором:

а) какой-либо из параметров состояния системы равен нулю;

б) какой-либо из параметров состояния системы изменяется;

в) какой-либо из параметров состояния системы не изменяется.

14. Равновесное состояние системы – это такое её состояние, при котором:

а) параметры состояния системы имеют определённые значения, постоянные при неизменных внешних условиях;

б) параметры состояния системы имеют определённые значения, постоянные при изменяющихся внешних условиях;

в) параметры состояния системы имеют изменяющиеся значения при неизменных внешних условиях;

г) параметры состояния системы имеют изменяющиеся значения при изменяющихся внешних условиях.

15. Время релаксации – это время, в течение которого:

а) система приходит в неравновесное состояние;

б) система приходит в равновесное состояние;

в) состояние системы не изменяется;

г) состояние системы изменяется.

16. Процесс – это переход системы из одного состояния в другое состояние, связанный с изменением хотя бы одного из ее параметров состояния. Состояние идеального газа определяется значениями параметров: Т_о, р_о, V_o, где Т – термодинамическая температура, р – давление, V – объем газа. Определенное количество газа перевели из состояния (р₀, V₀) в состояние (2p_o, V_o). При этом его внутренняя энергия:

а) увеличилась;

б) не изменилась;

в) уменьшилась.

17. Обратимый процесс – это процесс, при котором:

а) возможно осуществить обратный переход системы из конечного в начальное состояние через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

б) возможно осуществить обратный переход системы из конечного в начальное состояние через любые промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

в) возможно осуществить обратный переход системы из конечного в начальное состояние через те же промежуточные состояния при этом, по окончании процесса в окружающей среде или в самой системе происходят какие-либо изменения.

18. Необратимый процесс – это процесс, по окончании которого:

а) в окружающей среде или в самой системе происходят какие-либо изменения;

б) невозможно осуществить обратный переход системы в первоначальное состояние;

в) возможно осуществить обратный переход системы из конечного в начальное состояние через те же промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде.

19. Круговой процесс или цикл – это:

а) переход системы из начального в конечное состояние, а затем из конечного в начальное состояние через любые промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

б) переход системы из конечного в начальное состояние, а затем из начального в конечное состояние через любые промежуточные состояния так, чтобы не осталось никаких изменений в окружающей систему среде;

в) такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, возвращается в него вновь.

20. Любой круговой процесс состоит из процессов расширения и сжатия. При этом процесс расширения сопровождается:

а) работой, совершаемой системой;

б) работой, совершаемой над системой;

в) работой, совершаемой системой и над системой внешними силами.

21. Любой круговой процесс состоит из процессов расширения и сжатия. При этом процесс сжатия сопровождается:

а) работой, совершаемой системой;

б) работой, совершаемой над системой внешними силами;

в) работой, совершаемой системой и над системой внешними силами.

22. Динамические закономерности – это закономерности, подчиняющиеся:

а) одному дифференциальному уравнению, допускающиму существование единственного решения для каждого начального условия;

б) системам уравнений (в том числе дифференциальных, интегральных и др.), допускающих существование единственного решения для каждого начального условия;

в) одному интегральному уравнению, допускающиму существование единственного решения для каждого начального условия;

г) системам уравнений (в том числе дифференциальных, интегральных и др.), допускающих существование множество решений.

23. Статистические закономерности – это:

а) количественные закономерности, устанавливаемые статистическим методом, в котором рассматриваются лишь средние значения величин, характеризующих данную систему;

б) количественные закономерности, рассматривающие конкретную молекулярную модель, обусловленные математическими методами статистики, основанные на теории вероятностей;

в) количественные закономерности, устанавливаемые статистическим методом, в котором рассматриваются любые значения величин, характеризующих данную систему;

г) количественные закономерности, рассматривающие любую молекулярную модель, обусловленные математическими методами статистики, основанные на теории вероятностей.

24. Термодинамическая вероятность – это:

а) число способов, которыми может быть реализовано любое состояние макроскопической физической системы;

б) предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при изменяющихся внешних условиях;

в) число способов, которыми может быть реализовано данное состояние макроскопической физической системы;

г) предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях.

25. Флуктуации – это:

а) случайные отклонения физических величин от их среднего значения;

б) любые отклонения физических величин от их среднего значения;

в) случайные отклонения физических величин от их истинного значения;

г) любые отклонения физических величин от их истинного значения.

26. Молекула – это:

а) наименьшая часть вещества, обладающая его основными физическими свойствами и состоящая из атомов, соединенных между собой химическими связями;

б) наименьшая часть вещества, обладающая его основными химическими свойствами и состоящая из атомов, соединенных между собой химическими связями;

в) наименьшая часть вещества, обладающая его основными химическими свойствами и состоящая из атомов, без учёта химических связяй.

27. Атом – это:

а) часть вещества микроскопических размеров (микрочастица), наименьшая частица химического элемента, являющаяся носителем только его физических свойств;

б) часть вещества микроскопических размеров (микрочастица), наименьшая частица химического элемента, которая не является носителем его свойств;

в) часть вещества микроскопических размеров (микрочастица), наименьшая частица химического элемента, являющаяся носителем его свойств.

28. Атомная масса – это:

а) относительное значение массы атома, выраженное в системе СИ;

б) относительное значение массы атома, выраженное в атомных единицах массы;

в) относительное значение массы атома, выраженное в системе СГС.

29. Молекулярная масса – это:

а) относительное значение массы молекулы, выраженное в атомных единицах массы;

б) относительное значение массы молекулы, выраженное в системе СИ;

в) относительное значение массы молекулы, выраженное в системе СГС.

30. Молярная масса, масса вещества, взятого в количестве одного моля, определяется соотношением:

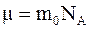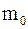а) , где – масса отдельной молекулы любого вещества;

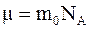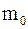б) , где – масса отдельной молекулы данного вещества;

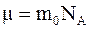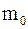в) , где – масса отдельной молекулы выбранного вещества.

31. Моль в единицах СИ – количество вещества. В одном моле вещества содержится столько молекул (атомов, ионов или каких-либо других структурных элементов вещества), сколько атомов:

а) содержится в 0,012 кг нуклида углерода атомной массы 12 (С¹²);

б) содержится в любом элементе;

в) содержится в 0,016 кг нуклида кислорода атомной массы 16 (С¹⁶).

2.2. Основные представления и законы
молекулярно-кинетической теории

1. Идеальный газ – это теоретическая модель газа, в которой:

а) не учитывается взаимодействие его частиц (средняя кинетическая энергия частиц намного больше энергии их взаимодействия);

б) принято считать, что размеры молекул идеального газа малы по сравнению с расстояниями между ними;

в) принято считать, что суммарный собственный объем молекул такого газа мал по сравнению с объемом сосуда;

г) принято считать, что силы взаимодействия между молекулами настолько малы, что движение молекул от столкновения до столкновения происходит по прямолинейным отрезкам. Число ежесекундных столкновений молекул мало.

2. Одно из основных положений молекулярно-кинетической теории идеального газа утверждает:

а) газ состоит из мельчайших частиц – атомов или молекул. Молекулы (атомы) газа свободно движутся между двумя последовательными взаимодействиями друг с другом или со стенками сосуда, в котором он находится;

б) газ состоит из мельчайших частиц – атомов или молекул, находящихся в непрерывном движении;

в) газ состоит из мельчайших частиц – атомов или молекул, находящихся в непрерывном движении. Направления и значения скоростей молекул газа самые различные;

г) газ состоит из мельчайших частиц – атомов или молекул, находящихся в непрерывном движении. Направления и значения скоростей молекул газа строго определённые.

3. Одно из основных положений молекулярно-кинетической теории идеального газа утверждает:

а) в любом, даже очень малом объёме, к которому применимы выводы молекулярно-кинетической теории, число молекул очень велико. Размеры молекул соизмеримы с расстояниями между ними;

б) в любом, даже очень малом объёме, к которому не применимы выводы молекулярно-кинетической теории, число молекул очень велико. Размеры молекул малы по сравнению с расстояниями между ними;

в) в любом, даже очень малом объёме, к которому применимы выводы молекулярно-кинетической теории, число молекул очень велико. Размеры молекул малы по сравнению с расстояниями между ними.

4. Одно из основных положений молекулярно-кинетической теории идеального газа утверждает:

а) силы взаимодействия между молекулами, кроме моментов соударения, пренебрежимо малы. Соударения молекул происходят с потерей механической энергии, т.е. по закону абсолютно неупругого взаимодействия;

б) силы взаимодействия между молекулами, кроме моментов соударения, пренебрежимо малы. Соударения молекул происходят без потерь механической энергии, т.е. по закону абсолютно упругого взаимодействия;

в) силы взаимодействия между молекулами в момент соударения пренебрежимо малы. Соударения молекул происходят без потерь механической энергии, т.е. по закону абсолютно упругого взаимодействия;

г) силы взаимодействия между молекулами в момент соударения пренебрежимо малы. Соударения молекул происходят с потерей механической энергии, т.е. по закону абсолютно неупругого взаимодействия.

5. Одно из основных положений молекулярно-кинетической теории идеального газа утверждает:

а) при отсутствии внешних сил молекулы газа распределяются равномерно по всему объёму;

б) под действием внешних сил молекулы газа распределяются равномерно по всему объёму;

в) при отсутствии внешних сил молекулы газа распределяются неравномерно по всему объёму.

6. Основное уравнение молекулярно-кинетической теории газов имеет вид 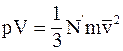, где :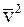

а) средняя арифметическая скорость молекул газа;

б) средняя квадратичная скорость молекул газа;

в) наиболее вероятная скорость молекул газа.

7. Основное уравнение молекулярно-кинетической теории газов для давления может быть записано в следующем виде:

а) ;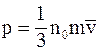

б) ;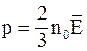

в) .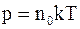

8. Закон Авогадро утверждает:

а) «В одинаковых объемах при разных температурах и давлениях содержатся одинаковые количества молекул»;

б) «В разных объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул»;

в) «В одинаковых объемах при одинаковых температурах и разных давлениях содержатся одинаковые количества молекул»;

г) «В одинаковых объемах при одинаковых температурах и давлениях содержатся одинаковые количества молекул».

9. Закон Дальтона утверждает:

а) «Давление смеси газов равно сумме тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один»;

б) «Давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, находился он один»;

в) «Давление смеси газов равно сумме парциальных давлений, т.е. тех давлений, которые имел бы каждый из входящих в смесь газов, если бы в объеме, занятом смесью, не находился он один».

10. На рисунке 1 в координатах p, V представлены изопроцессы, возможные в идеальных газах. Изотермическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.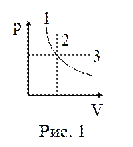

11. На рисунке 1 в координатах p, V представлены изопроцессы, возможные в идеальных газах. Изобарическому соответствует зависимость:

а) 1; б) 2; в) 3.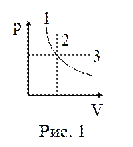

12. На рисунке 1 в координатах p, V представлены изопроцессы, возможные в идеальных газах. Изохорическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.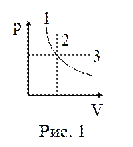

13. На рисунке 1 в координатах p, Т представлены изопроцессы, возможные в идеальных газах. Изотермическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.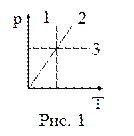

14. На рисунке 1 в координатах p, Т представлены изопроцессы, возможные в идеальных газах. Изобарическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.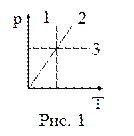

15. На рисунке 1 в координатах p, Т представлены изопроцессы, возможные в идеальных газах. Изохорическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.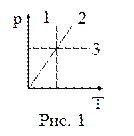

16. На рисунке 1 в координатах V, Т представлены изопроцессы, возможные в идеальных газах. Изотермическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.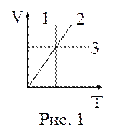

17. На рисунке 1 в координатах V, Т представлены изопроцессы, возможные в идеальных газах. Изобарическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.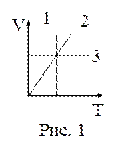

18. На рисунке 1 в координатах V, Т представлены изопроцессы, возможные в идеальных газах. Изохорическому процессу соответствует зависимость:

а) 1; б) 2; в) 3.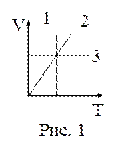

19. На рисунке 1 представлена зависимость давления газа от температуры при его нагревании. Сжимался или расширялся газ при нагревании?

а) сжимался; б) расширялся; в) объём газа не изменялся.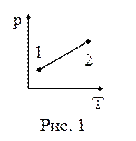

20. Горелками, дающими за равные промежутки времени одинаковое количество теплоты, нагревались одинаковые массы воды, меди и железа. На рисунке 1 представлены зависимости изменения температуры данных веществ от времени. Изменению температуры воды от времени соответствует график:

а) 1; б) 2; в) 3.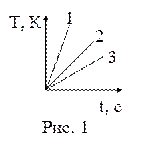

21. Горелками, дающими за равные промежутки времени одинаковое количество теплоты, нагревались одинаковые массы воды, меди и железа. На рисунке 1 представлены зависимости изменения температуры данных веществ от времени. Изменению температуры железа от времени соответствует график:

а) 1; б) 2; в) 3.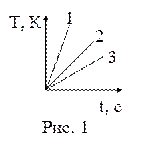

22. Горелками, дающими за равные промежутки времени одинаковое количество теплоты, нагревались одинаковые массы воды, меди и железа. На рисунке 1 представлены зависимости изменения температуры данных веществ от времени. Изменению температуры меди от времени соответствует график:

а) 1; б) 2; в) 3.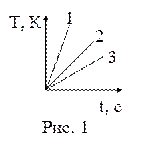

2