Классификация структур данных, применяемых при программировании.
Говоря о строении данных, нужно понимать, что данные представляют собой некоторую информацию, причем информацию с некоторым уровнем абстракции. Этот уровень определяется решаемой задачей. Например, вычисляя средний балл сдачи группой экзамена, нас совсем не интересует пол студента или его фамилия. Но ситуация меняется в случае изменения постановки задачи: кто из студенток сдал экзамен с оценкой «отлично»?
В любом случае, данные представляют некоторую абстракцию некоторого фрагмента реального мира. Решая любую задачу необходимо выбрать уровень абстрагирования, т.е. определить множество данных, представляющих реальную ситуацию. При выборе следует руководствоваться той задачей, которую необходимо решить. Затем надлежит выбрать способ представления этой информации. Здесь уже необходимо ориентироваться на те средства, с помощью которых решается задача. В большинстве случаев эти два этапа не бывают полностью независимыми.
Способ представления данных определяется используемым языком программирования. Вместе с тем, очевидно, что данные могут быть как простыми (однородными), так и сложными, структурированными, не имеющими прямого отражения в предоставляемых типовых данных языка программирования. Определим несколько основных строительных конструкций – структур данных, которые назовем фундаментальными структурами. Согласно Вирту – одному из основателей теории структур данных – такими фундаментальными структурами будут: записи (структуры в терминологии языка Си); массивы фиксированного размера и множества. Отметим, что эти «строительные блоки» соответствуют математическим понятиям, отражающим фундаментальные идеи.
Краеугольным камнем всей теории структур данных является различие между фундаментальными и производными структурами. Фундаментальные структуры – это молекулы (в свою очередь состоящие из атомов), из которых строятся производные структуры. Элементы фундаментальных структур могут изменять только свое значение, а структура их и множество допустимых значений остается неизменными. В результате размер памяти, занимаемый такими элементами, остается постоянным. В дальнейшем, для определения фундаментальных структур будем использовать термин статические структуры данных. В отличие от них, для элементов производных структур характерна способность изменять в процессе выполнения программы не только свое значение, но и саму структуру. Далее для таких структур будем использовать термин динамические структуры данных.
4. Классические алгоритмы сортировки и поиска.
Среди всего множества алгоритмов существует класс так называемых алгоритмов сортировки. В рамках исследования алгоритмов этого класса представлено много различных методов решения одной и той же задачи. Математический анализ некоторых из алгоритмов подчеркивает их недостатки и достоинства и помогает программисту осознать важность такого анализа при выборе способа решения поставленной задачи. В целом, класс алгоритмов сортировки представляет собой идеальный объект для иллюстрации многих принципов программирования и ситуаций, встречающихся в других задачах. Задача сортировки – это задача упорядочивания некоторого массива данных. Например, массив {121, 80, 45, 29, 324, 2, 8} требуется преобразовать к виду {2, 8, 29, 45, 80, 121, 324}.
Глубина проработки материала, связанного с представленной задачей, позволяет говорить об алгоритмах сортировки как о классических алгоритмах теории структур данных.
Другими алгоритмами, ставшими к настоящему времени классическими, несомненно, следует отнести алгоритмы поиска заданной информации в представленном массиве данных. Существуют разные постановки такой задачи, одна из которых, например, может быть определена так:
«в заданном тексте Т найти фразу Ф».
5. Понятие сложности алгоритма, оценки времени исполнения.
Создавая и исследуя алгоритмы, необходимо выполнять оценку качества найденных решений. В большинстве случаев такая оценка в первую очередь связана с производительностью алгоритмов, или, что в некотором смысле то же самое – со временем работы реализующей алгоритм программы.
 Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный способ – это просто запустить реализующую исследуемый алгоритм программу на нескольких наборах исходных данных и сравнить время исполнения. Другой способ - оценить время исполнения. Например, можно утверждать, что время поиска оценивается как O(n) (читается так: «О большое от n»).
Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный способ – это просто запустить реализующую исследуемый алгоритм программу на нескольких наборах исходных данных и сравнить время исполнения. Другой способ - оценить время исполнения. Например, можно утверждать, что время поиска оценивается как O(n) (читается так: «О большое от n»).
Когда используют обозначение O(), имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n2), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов. Чтобы почувствовать, что это такое, приведены числа, иллюстрирующие скорость роста для нескольких разных функций.
| n | log n | n*log n | n2 |
| 2 048 | 65 536 | ||
| 4 096 | 49 152 | 16 777 216 | |
| 65 536 | 1 048 565 | 4 294 967 296 | |
| 1 048 476 | 20 969 520 | 1 099 301 922 576 | |
| 16 775 616 | 402 614 784 | 281 421 292 179 456 |
Если считать, что числа в таблице соответствуют микросекундам, то для задачи с 1048476 элементами алгоритму с временем работы O(log n) потребуется 20 микросекунд, а алгоритму с временем работы O( n2 ) - более 12 дней.
Рассмотрим задачу сложения двух матриц. Например
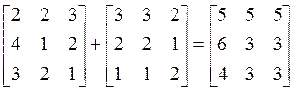
Сколько операций сделано?
2+3 = 5 всего 2 операции и так делали 9 = 32 раз. В этом случае повторение отдельного шага α+β=γвыполняется9 раз. Если обозначить длину строки через n, то получаем формулу для подсчета числа операций, выполняемых при сложении матриц в общем случае
<количество операций> = 2*n2
Здесь 2 – некоторый постоянный коэффициент и видим квадратичную зависимость от объема исходных данных О(n2).
Рассмотрим задачу умножения двух матриц. Например
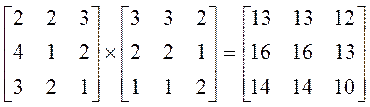
Сколько операций сделано?
2*3 + 2*2 + 3*1 = 13 и так делали 32 раз. Здесь уже «цена» отдельного шага зависит от размерности исходных данных: n операций умножения и n операций сложения и записи, т.е. 2*n операций.
Тогда общая сложность алгоритма есть 2*n3и имеем алгоритм кубической сложности О(n3).
Если оба алгоритма, например, O ( n*log n ), то это отнюдь не значит, что они одинаково эффективны.
Символ О не учитывает константу, то есть первый может быть, скажем в 1000 раз эффективнее. O() значит лишь то, что их время возрастает приблизительно как функция n*log n.
За функцию берется количество операций, возрастающее быстрее всего.
То есть, если в программе одна функция выполняется O(n) раз - например, умножение, а сложение - O(n2) раз, то общая сложность программы - O(n2), так как в конце концов при увеличении n более быстрые ( в определенное, константное число раз ) сложения станут выполняться настолько часто, что будут влиять на быстродействие куда больше, нежели медленные, но редкие умножения. O() показывает исключительно асимптотику !
Основание логарифма не пишется.
Причина этого весьма проста. Пусть есть O( log2 n). Но log2 n=log3 n / log3 2, а log3 2, как и любую константу, асимптотика - символ О() не учитывает. Таким образом, O(log2 n) = O(log3 n).
6. Общие подходы к проектированию алгоритмов из различных проблемных областей.
Прежде всего – это общая технология проектирования. Технология предполагает прежде всего определенную последовательность действий, выполняемую при помощи заданных инструментов.
В нашем случае:
- анализ поставленной задачи, определение используемых исходных данных и результата ее решения;
- разработка форм представления используемых в задаче данных;
- декомпозиция задачи - выявление отдельных подзадач, решение которых в совокупности обеспечивает решение общей задачи;
- анализ отдельных подзадач и построение алгоритмов их решения;
- кодирование программ, реализующих алгоритмы решения отдельных подзадач и общей задачи;
- отладка полученной программы;
- оценка скорости получения и качества находимых программой решений;
- подготовка сопроводительной документации к созданному программному продукту.
Вообще говоря, каждый из приведенных шагов предполагает как соответствующую инструментальную поддержку, так и возможность возврата на предыдущие этапы с целью модификации принятого там решения. Очевидно, что в представленном перечне приведены не все шаги – могут быть и другие – с одной стороны, а с другой стороны – не все из представленных шагов на практике выделяются отдельно – часто они объединены в один процесс.
Вычислительные алгоритмы.
1. Математика и алгоритмы.
Как и вся информатика в целом, само понятие алгоритма появилось из недр математики. Теория чисел, тория вычислений, математическая логика и ряд других математических дисциплин легли в основу теории алгоритмов.
Теория алгоритмов – это раздел математики, в котором изучаются теоретические возможности эффективных процедур вычисления и их приложения. Основное понятие теории – понятие алгоритма в интуитивном понимании существует в математике довольно давно. Под алгоритмом понимают точное предписание для совершения некоторой последовательности элементарных действий над исходными данными любой задачи из некоторого класса однотипных задач, в результате которой получится решение этой задачи.
Примером алгоритма может служить правило нахождения НОД двух чисел (алгоритм Эвклида). Формула для нахождения корней квадратного уравнения также является своеобразной формой записи алгоритма. Она показывает, какие арифметические операции и в какой последовательности нужно производить над коэффициентами квадратного уравнения, чтобы получить его корни.
Точные математические понятия, формализующие интуитивное понятие алгоритма, были предложены в 30гг. 20 века. Отметим только, что эти результаты были получены такими учеными, как Гедель, Клини, Черч, Пост, Тьюринг, Марков, Колмогоров. Ряд результатов основывается на математической теории рекурсивных функций, ряд – на абстрактной модели вычислительной машины.
Общими характеристиками алгоритма являются:
- детерминированность (определенность) – однозначность результата процесса при заданных исходных данных;
- дискретность определяемого алгоритмом процесса – расчлененность его на отдельные элементарные акты;
- массовость – исходные данные для алгоритма можно выбирать из некоторого множества данных (потенциально бесконечного), т.е. алгоритм должен обеспечивать решение любой задачи из класса однотипных задач.
К сожалению, и до настоящего времени существуют задачи, не имеющие алгоритма решения, хотя теоретически установлено наличие такового.
2. Общая классификация вычислительных алгоритмов.
Общепринятой классификации множества вычислительных алгоритмов не существует, как неоднообразно и само определение вычислительного алгоритма. Будем понимать под «вычислительными» алгоритмы, используемые для вычисления математических объектов: констант, функций, нахождения корней различного типа уравнений и систем уравнений.
Условно все вычислительные алгоритмы можно поделить на два класса: основанные на представлении данных целочисленными значениями либо использующими плавающую арифметику.
По области применения для такого рода алгоритмов можно выделить такие области как
- теория чисел, быстрые алгоритмы вычисления различных констант и распространенных математических функций;
- решение алгебраических задач;
- нахождение корней различного рода уравнений;
- приближение функций;
- вычислительная геометрия;
- и ряд других.
3. Точность представления чисел. Вычисление «машинного нуля».
Одной из проблем, встречающихся при программировании алгоритмов вычислительного характера, является точность представления чисел в памяти компьютера. Вы уже знаете, что в языке Си, для представления вещественных чисел используются типы данных float, double и long double, при этом оказывается задействованными 4, 8 и 10 байтов соответственно.
Следует сразу заметить, что тип float может использоваться только в очень ограниченных ситуациях. Для того, чтобы в этом убедиться достаточно выполнить простую программу:
#include <stdio.h>
#include <conio.h>
void main()
{
float a, b,c,d,e,f;
a=95.0;
b=(float)0.2;
d = (a+b)*(a+b);
e = (float)-2.0*a*b -a*a;
f = b*b;
c = (d+e) / f;
printf ("\nc=%f\n",c);
getch();
}
(a+b)*(a+b)=a2+2ab+b2-2ab- a2b2
(a2+2ab+b2 – 2ab – a2) / b2
Результат: с=1.000976
Ясно, что это связано с возможностью дискретизации числового ряда. Значение 95.0 фактически представляется в памяти как 00 00 BE 42, а значение 0.2 последовательностью CD CC 4C 3E.
Фактически тип float может использоваться только для представления исходных данных или конечных результатов, но использовать его для промежуточных вычислений, особенно в итерационных алгоритмах – нельзя.
Вторым вопросом, который очень существенен при построении программ для алгоритмов вычислительного характера, является так называемая «оценка машинного нуля». Дело в том, что при организации вычислений очень часто завершение работы алгоритма производится при достижении заданной точности, т.е. числового значения, меньше которого невозможно задавать точность данного алгоритма. Обычно, такое условие задается некоторой формулой типа |xi+1-xi|<ε.
Указанное абсолютное значение зависит от разрядной сетки применяемого компьютера, от способа представления вещественных чисел в используемом компиляторе языка программирования и от самих значений, используемых для оценки точности. Далее представлена программа, которая оценивает абсолютное значение «машинного нуля» относительно близких к единице переменных типа float:
#include <stdio.h>
#include <conio.h>
Void main()
{
int i=0;
float res=1.0, work;
do
{
i++;
res = res/(float)2.0;
work = res+(float)1.0;
} while (work>1.0);
printf ("\nNumber of divisions =%6d\n",i);
printf ("\nprecision =%.10f\n",res);
getch();
}
Результат работы этой программы выглядит как
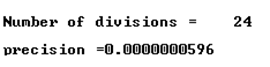
Подобная программа для переменных типа дает такой результат:
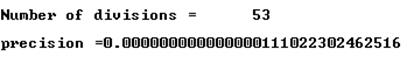
В заголовочном файле LIMITS.H приведены различные предельные значения для констант разных типов.
Наконец, третей проблемой, с которой сталкиваются разработчики программ, является ситуация, когда вычисления по какой-то формуле вообще не могут быть выполнены ввиду ограничений на представление вещественных чисел. Например, пусть p – некоторое число, лежащее на интервале [0,1] (вероятность) и задана некоторая достаточно большая последовательность таких чисел. Эта последовательность характеризует множество объектов, которые можно разбить на классы D с одинаковым значением p = pi. Пронумеруем полученные классы в порядке возрастания pi и пусть qj – количество объектов из класса Dj. Для любого класса Dj математическое ожидание Mj, оценивается по формуле Mj = qj pjm, и m – общее количество элементов. Тогда аналогичная величина для объединения классов D1 ,D2 ,..,Dk : 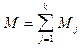 .
.
Если предположить, что общее количество элементов – несколько тысяч, то ясно, что вычисления в «лоб» ничего хорошего не дадут – возводя в тысячную степень число, взятое с интервала [0,1], будем получать нули! Один из приемов, который можно применить в данном случае – это заменить вычисление Mj = qj pjm, на вычисление эквивалентного ему уравнения log(Mj )=log( qj pjm), поскольку log( qj pjm)= log( qj)+ log(pjm)= log( qj)+ m log(pj) – а это уже вполне представимое значение.
4. Вычисление функций разложением в ряд.
Одним из самых распространенных типов вычислительных алгоритмов является тип вычисления значений некоторой аналитической функции: sin(x), tg(x), ex и т.п. Конечно, существуют стандартные подпрограммы (функции библиотеки С) позволяющие получить значения указанных функций, но чтобы, во-первых, понять, как они устроены, а, во-вторых, научиться решать задачу для функций, не поддержанных набором стандартов, рассмотрим алгоритм вычисления функции y=ex более подробно.
Вам из курса математического анализа должно быть известно, что эта функция приближенно может быть вычислена как сумма ряда
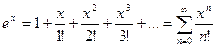
Воспользуемся этой формулой для вычисления приближенного значения функции.
Прежде всего заметим, что каждый следующий член ряда mi+1 может быть получен по формуле mi+1= mi*x/i. Тогда программа, реализующая вычисления, может выглядеть следующим образом:
#include <stdio.h>
#include <math.h>
#include <conio.h>
Void main()
{
Дата добавления: 2022-02-05; просмотров: 412;











