Мощность множеств. Кардинальные числа.
Конечное множество – множество, состоящее из конечного числа элементов.
Пример. A = {1, 2, 3, 4, 5}.
Основной характеристикой конечного множества является число его элементов. Мощностью конечного множества называют число его элементов.
Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислить количество элементов других множеств, которые составлены из первых с помощью некоторых операций.
Бесконечное множество – множество, не являющееся конечным.
Понятие мощности бесконечного множества является гораздо более сложным и не дано в настоящем документе.
Пример. Множество натуральных чисел является бесконечным.
Кардинальное число множество – мощность этого множества.
Если между множеством А и множеством В можно установить взаимно однозначное соответствие (то есть биекцию), то говорят, что эти множества эквивалентныи пишутА ~ В. Очевидно, эквивалентные множества имеют одинаковую мощность.
Счетные множества
Пусть N – множество всех натуральных чисел N={1, 2, 3, . . .}, тогда всякое множество А, эквивалентное множеству N, будет называться счётным множеством.
Пример. А={1, 4, 9, 16, . . . ,n 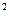 , . . .}; B={3, 6, 9, 12, . . . ,3n, . . . }.
, . . .}; B={3, 6, 9, 12, . . . ,3n, . . . }.
Наименьшей бесконечной мощностью является 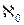 (алеф ноль) — мощность множества натуральных чисел.
(алеф ноль) — мощность множества натуральных чисел.
Теорема (необходимое и достаточное условие счетности множества). Для того чтобы множество Х было счётным необходимо и достаточно, чтобы его можно было представить в форме последовательности:
Х={x 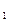 , x
, x 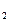 , x
, x 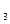 , …, x
, …, x 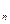 , …} (*).
, …} (*).
Доказательство необходимости. Пусть множество Х счетное, то из определения счётного множества следует существование взаимно однозначного соответствия j между множеством Х и множеством натуральных чисел N. Достаточно обозначить через х 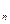 , тот из элементов множества Х, который в соответствии с j отвечает числу n,чтобы получить представление множества Х в форме (*).
, тот из элементов множества Х, который в соответствии с j отвечает числу n,чтобы получить представление множества Х в форме (*).
Доказательство достаточности. Если множество Х представлено в форме (*), то достаточно каждому его элементу х, соотнести индекс n этого элемента, чтобы получить взаимно однозначного соответствия j между множеством Х и множеством натуральных чисел N, так что из определения счётного множества следует, что множество Х счётное.
Понятно, что все счетные множества эквивалентны между собой.
Свойства счетных множеств:
1. Всякое подмножество счетного множества конечно либо счетно.
2. Объединение конечного либо счетного множества счетных множеств конечно либо счетно.
3. Всякое бесконечное множество содержит счетное подмножество.
4. Если к бесконечному множеству А присоединить конечное либо счетное множество В, то от этого мощность множества не изменится: АÈВ ~ А.
Дата добавления: 2022-02-05; просмотров: 393;











