Классические формулировки парадокса Рассела.

Предпосылки аксиоматического построения теории множеств

До второй половины XIX века понятие “множества” не рассматривалось в качестве математического (“множество книг на полке”, “множество человеческих добродетелей” и т.д.— всё это чисто бытовые обороты речи). Положение изменилось, когда немецкий математик Георг Кантор разработал свою программу стандартизации математики, в рамках которой любой математический объект должен был оказываться тем или иным “множеством”. При этом общее понятие “множество”, которое Кантор считал центральным для математики, он рассматривал как “многое, мыслимое как единое”. Это вполне соответствовало умонастроению самого Кантора, подчёркнуто называвшего свою программу не “теорией множеств” (этот термин появился много позднее), а учением о множествах (Mengenlehre).

Программа Кантора вызвала резкие протесты со стороны многих современных ему крупных математиков. Особенно выделялся своим непримиримым к ней отношением Леопольд Кронекер, полагавший, что математическими объектами могут считаться лишь натуральные числа и то, что к ним непосредственно сводится (известна его фраза о том, что “бог создал натуральные числа, а всё прочее — дело рук человеческих”). Тем не менее, некоторые другие математики — в частности, Готлоб Фреге и Давид Гильберт — поддержали Кантора в его намерении перевести всю математику на теоретико-множественный язык.

В начале XX века Бертран Рассел, изучая наивную теорию множеств, пришел к парадоксу (с тех пор известному как парадокс Рассела). Таким образом, была продемонстрирована несостоятельность наивной теории множеств и, связанной с ней, канторовской программы стандартизации математики.

Парадокс Рассела. Пусть X – множество всех множеств, которые не являются собственными элементами. Тогда X в том и только том случае является собственным элементом, когда оно не является собственным элементом.

Доказательство. Предположим, что XÎX. Тогда X является собственным элементом и, значит, не входит в X по определению X. Таким образом, XÎXÞXÏX. С другой стороны, если XÏX то X не является собственным элементом и, значит, входит в X по определению X. Таким образом. XÏXÞ XÎX.

Классические формулировки парадокса Рассела.

Парадокс Рассела можно сформулировать и не используя теорию множеств. Вот три классические формулировки этого парадокса.

Парадокс парикмахера. Вождь афинской демократии Клисфен повелел, чтобы единственный парикмахер города брил тех и только тех граждан Афин, которые не бреются сами. Должен ли парикмахер брить себя?

Парадокс каталога. Библиотека Борхеса решила составить библиографиче­ский каталог, в который входят те и только те каталоги, которые не включают себя. Включает ли такой каталог себя?

Парадокс самоуважения. Имеет ли профессор Конте самоуважение, если он уважает только тех, кто не уважает себя?

Объяснение логических парадоксов. Легко видеть, что в действительности все эти парадоксы не содержат в себе ничего парадоксального и математики повседневно сталкиваются с подобными ситуациями. Чтобы объяснить, в чем тут дело, дадим еще одну эквивалентную формулировку парадокса Рассела.

Парадокс Пиглета. Пусть п - такое целое число, которое одновременно больше и меньше нуля. Тогда п в том и только том случае является положительным, когда оно является отрицательным.

Но ведь такого числа не существует. Именно так: все “логические парадоксы” (не путать с “лингвистическими” или “семантическими” парадоксами, типа парадокса лжеца) построены по следующей схеме: предположим, что существует некоторый объект X. Тогда этот объект X одновременно обладает и не обладает некоторым свойством. Но это в точности и значит, что требуемого объекта X не существует, именно так устроены доказательства от противного, например, доказательство иррациональности числа 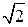или бесконечности множества простых чисел. Единственная разница состоит в том, что в парадоксе Пиглета противоречивость условия очевидна сразу, а в парадоксе Рассела условие не кажется противоречивым - хотя и является таковым. Таким образом, парадокс Рассела всего лишь доказывает (от противного), что не существует множества Y={X|XÏX}всех множеств, не являющихся собственными элементами, и, тем самым, не для любого свойства Р обязано существовать множество {х|Р(х)}. Но никто из серьезных математиков никогда и не утверждал, что любое свойство должно определять множество.

Парадокс бесконечности.Построим бесконечное множество следующим образом: на каждом шаге в множество будем добавлять два элемента из натурального ряда, и после этого убирать первый в порядке следования. Получим следующую схему:

{1, 2}; {2}; {2, 3, 4}; {3, 4}; {3, 4, 5, 6}; {4, 5, 6}…

Возникает вопрос: сколько элементов будет в этом бесконечном множестве? Количество элементов возрастает. Но на первом шаге мы убрали из множества первый элемент, на втором шаге – второй и так далее. Если рассматривать каждый конкретно взятый элемент, то окажется, что его нет во множестве (ведь nÞ¥).

На самом деле парадокса тут никакого нет. Все дело в том, что бесконечные множества устроены существенно сложнее конечных, и интуиция тут не всегда срабатывает правильно.

Столкнувшись с этими парадоксами, создатели теории множеств осознали, что нельзя задавать множества произвольными словосочетаниями.

Часть математиков (например, Л. Э.Я. Брауэр и его школа) вообще решила полностью отказаться от использования теоретико-множественных представлений. Другая же часть математиков, возглавленная Д. Гильбертом, предприняла ряд попыток обосновать ту часть теоретико-множественных представлений, которая казалась им наименее ответственной за возникновение антиномий, на основе заведомо надёжной финитной математики. С этой целью были разработаны различные аксиоматизации теории множеств. Особенностью аксиоматического подхода является отказ от, лежащего в основе программы Кантора, представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества “существуют” исключительно формальным образом, и их «свойства» могут существенно зависеть от выбора аксиоматики.

Современная теория множеств строится на системе аксиом — утверждений, принимаемых без доказательства, из которых выводятся все теоремы и утверждения теории множеств.

Одной из наиболее популярных аксиоматик является система аксиом Цермело — Френкеля (ZF). Эта и подобные ей системы аксиом любопытны потому, что любая математическая теория может быть «переведена» на язык теории множеств таким образом, что теоремы этой теории станут теоремами о множествах, доказуемыми из аксиом ZF.

Система аксиом Цермело-Френкеля дает доказывает существование некоторых множеств и дает способ их получения.

1. Аксиома объемности. Если два множества имеют одни и те же элементы, они тождественны.

"A, B: A=B Û "c, cÎAÛ cÎB.

2. Аксиома пустого множества. Существует пустое множество Æ, которое не содержит элементов.

$Æ: "a, aÏÆ.

3. Аксиома пары. Для любых множеств A и B существует множество C такое, что A и B являются его единственными элементами. Множество C обозначается {A, B} и называется неупорядоченной парой A и B. Если A = B, то C состоит из одного элемента.

"A, "B, $C: "D, DÍCÛ(D=A Ú D=B).

4. Аксиома объединения. Для любого множества A существует множество B=a₁Èa₂È…Èa_n – объединение всех элементов множества A, состоящее из тех и только тех элементов, которые содержатся в элементах множества А.

"A, $B: "C, CÍB Û $D, (CÍD Ù DÍA).

5. Аксиома бесконечности. Существует множество, которое содержит ∅ в качестве своего элемента, и такое, что если а есть элемент этого множества, тогда последовательность aÈ{a} есть также элемент этого множества.

$w: ÆÎw Ù "x, xÎw Þ {x,{x}}Îw.

6. Аксиома регулярности. Если A – непустое множество, тогда имеется подмножество В множества A, такое, что не имеется множеств, которые принадлежат обоим множествам А и В.

7. Аксиома выделения. Любому множеству A и свойству j отвечает множество B, элементами которого являются те и только те элементы A, которые обладают свойством j.

"A $B: "c, cÎB Û (cÎA Ù j(c)).

8. Аксиома основания. Каждое непустое множество S содержит подмножество A такое, что SÇA=Æ.

"S, S¹Æ Þ $A, AÍS Ù AÇS=Æ.

9. Аксиома выбора. Для любого семейства попарно непересекающихся непустых множеств существует множество C такое, что, каково бы ни было множество X данного семейства, множество состоит из одного элемента.

Вопрос об аксиоме выбора является одним из самых спорных и обсуждаемых до сих пор.

Кроме аксиоматики Цермело-Френкеля, популярной является аксиоматика Фон-Неймана.