Лекция № 8. Логические функции.

Ниже будет подробно рассматриваться двухэлементное множество 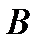и двоичные переменные, принимающие значения из этого множества. Его элементы часто обозначают 0 и 1, однако они, вообще говоря, не являются числами в обычном смысле (хотя и похожи на них по некоторым свойствам). Наиболее распространённая интерпретация двоичных переменных – логическая: “да” – “нет”, “истинно” – “ложно”. В контексте, содержащем одновременно двоичные и арифметические величины, а также функции, эта интерпретация обычно фиксируется явно. Например, в языках программирования (Pascal и др.) вводится специальный тип переменной – логическая переменная, значения которой обозначаются true и false. В данной лекции логическая интерпретация двоичных переменных не везде является обязательной, поэтому будем считать, что 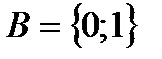, рассматривая 0 и 1 как формальные символы, не имеющие арифметического смысла.

1. Функции алгебры логики.

Определение. Алгебра, образованная множеством 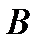вместе со всеми возможными операциями на нём, называется алгеброй логики.

Определение. Функцией алгебры логики (логической функцией) называется 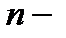арная операция на множестве .

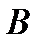Первый термин является более точным, однако второй более распространён, особенно в приложениях. Он и будет использоваться в дальнейшем. Итак, логическая функция 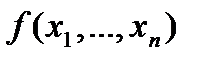- это функция, принимающая значения 0 или 1. Множество всех логических функций будем обозначать 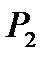, множество всех логических функций 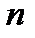переменных - .

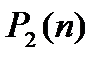Определение. Алгебра, образованная 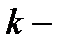элементным множеством вместе со всеми операциями на нём, называется алгеброй 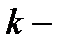значной логики, а 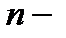арная операция на 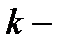элементном множестве называется 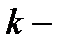значной логической функцией.

Множество всех 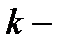значных логических функций обозначается 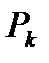. Мы в дальнейшем будем рассматривать логические функции только из .

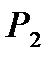Всякая логическая функция 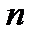переменных может быть задана таблицей, в левой части которой перечислены все наборы значений переменных (которых всего 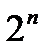), а в правой части – значение функции на этих наборах значений. Ниже приведена таблица, задающая некоторую функцию трёх переменных.

Наборы, на которых значение функции равно 1, часто называют единичными наборами функции 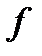, а множество единичных наборов называют единичным множеством функции 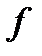. Аналогично, наборы, на которых значение функции равно 0, называют нулевыми наборами функции 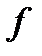. В приводимой таблице три единичных набора и пять нулевых наборов.

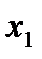
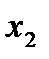
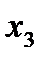
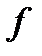
Таблица 1.

Заметим, что наборы в таблице расположены в определённом порядке – лексикографическом, который совпадает с возрастанием наборов, если рассматривать их как двоичные числа. Этим упорядочением будем пользоваться в дальнейшем. При любом фиксированном упорядочении наборов логическая функция 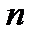переменных полностью определяется вектор-столбцом значений функции, то есть 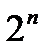. Поэтому число различных функций 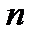переменных равно числу различных двоичных векторов длины .

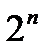Определение. Переменная 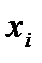в функции 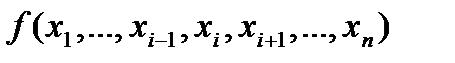называется несущественной (фиктивной), если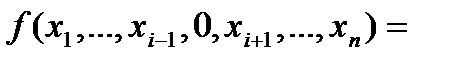 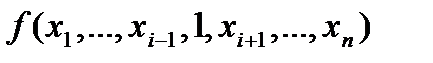при любых значениях остальных переменных.

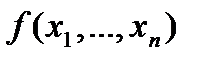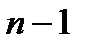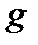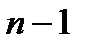Иначе говоря, переменная считается несущественной, если изменение её значения в любом наборе не изменяет значения функции. В этом случае функция по существу зависит от переменной, то есть представляет собой некоторую функцию от переменной. Говорят, что функция 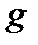получена из функции 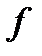удалением фиктивной переменной или, наоборот, что функция 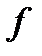получена из функции 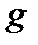добавлением фиктивной переменной. Например, запись 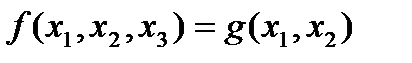означает, что при любых значениях 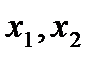выполняется 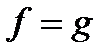независимо от значения .

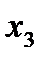Практический смысл удаления фиктивных переменных очевиден, поскольку они не влияют на значение функции и являются с этой точки зрения лишними. Однако иногда бывает полезно вводить фиктивные переменные. Благодаря такому введению можно всякую функцию 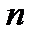переменных сделать функцией любого большего числа переменных. Поэтому любую конечную совокупность функций можно считать зависящей от одного и того же множества переменных (которое является объединением множеств переменных всех взятых функций).

1. Примеры логических функций.

Логических функций одной переменной четыре; они приведены в таблице 2.

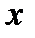
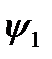
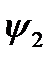
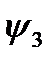
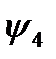
Таблица 2.

Здесь функци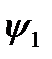и и 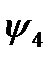- константы 0 и 1 соответственно, значения которых не зависят от значения переменной, и, следовательно, переменная 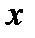для них несущественна. Значения функции 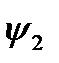совпадают со значениями переменной 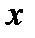. Наконец, функция 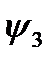, значения которой противоположны значениям переменной, есть ни что иное, как отрицание 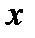(функция НЕ). Различные способы обозначения этой функции: .

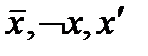Логических функций двух переменных – шестнадцать; они приведены в таблице 3.

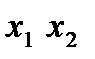
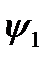
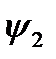
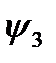
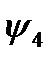
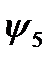
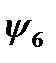
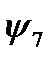
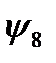
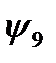
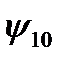
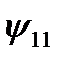
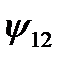
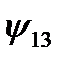
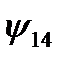
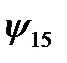
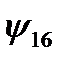
0 0
0 1
1 0
1 1

Таблица 3.

Функци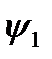и и 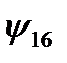, как и в предыдущем случае являются константами, то есть функциями с двумя несущественными переменными. Отметим, что формально эти функции отличаются от функци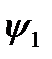й и 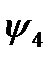из предыдущего примера, поскольку являются бинарными операциями на множестве 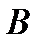. Однако ранее было принято функции, отличающиеся только несущественными переменными, считать равными.

Среди представленных в таблице 3 функций отметим те, которые уже знакомы нам в качестве логических операций, изученных в ходе предыдущей лекции.

Функция 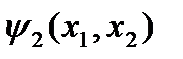является конъюнкцией переменных 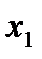и 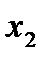(функцией И). Она равна 1 тогда и только тогда, когда обе переменные равны 1. Обозначается: 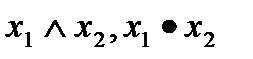, 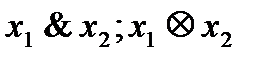. Её также называют логическим умножением, поскольку таблица её действительно совпадает с таблицей обычного умножения для чисел 0 и 1. Поэтому, кстати, по аналогии с обычным умножением, знак операции между переменными часто опускают: .

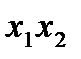Операцию будем называть умножением по модулю 2 (см. ниже). Она реализует произведение остатков от деления чисел 0 и 1 на число 2.

Функция 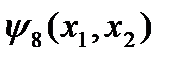называется дизъюнкцией переменных 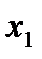и 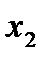(функцией ИЛИ). Она равна 1, если значения 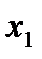или 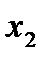равны 1. Союз “или” понимается здесь в неразделительном смысле “хотя бы один из двух”. Обозначается: .

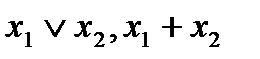Функция 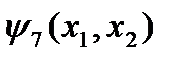называется неравнозначностью переменных 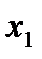и 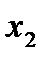. Она равна 1, когда значения аргументов различны, и равна 0, когда значения аргументов одинаковы. Обозначается: .

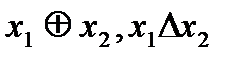Привести пример такой функции более сложно. Для этого введём следующее понятие, широко используемое в теории чисел.

Два целых числа 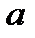и 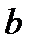называются сравнимыми по модулю 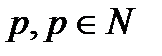, если при делении на это число они дают одинаковые остатки.

Обозначается: 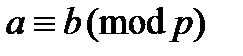. Например, 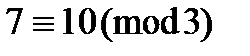, 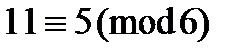. Так вот, функцию 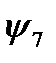можно рассматривать, как сложение по модулю 2. Действительно, сумма остатков от деления чисел 0 и 1 на число 2 равна 1, а сумма остатков от деления чисел 0 и 0, либо 1 и 1 на 2 равна 0.

Функция 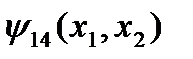называется импликацией или логическим следованием. Обозначается: .

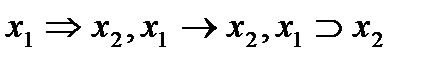Функция 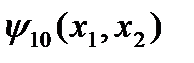называется эквивалентностью или равнозначностью. Она равна 1, если значения переменных одинаковы и 0, если они различны. Обозначается: .

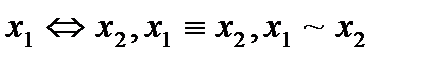Есть ещё две функции двух переменных, имеющие специальные названия. Функция 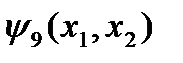называется стрелкой Пирса и обозначается 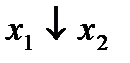. Функция 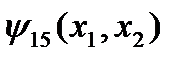называется штрихом Шеффера и обозначается 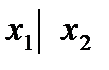. Остальные функции специальных названий не имеют и, как можно показать, легко выражаются через перечисленные выше функции.

В функциях 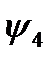и 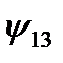переменная 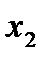фиктивна. Из таблицы 3 видно, что 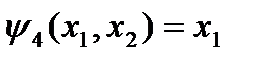, а 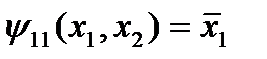. Аналогично, в функциях 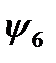и 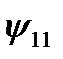переменная 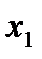фиктивн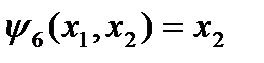а: , а .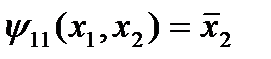

Доказано, что с ростом числа переменных 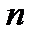доля функций, имеющих фиктивные переменные, убывает и стремится к нулю.

1. Суперпозиции и формулы.

Ранее было введено определение суперпозиции функций, согласно которому суперпозицией нескольких функций называлась новая функция, полученная с помощью подстановок данных функцией друг в друга и переименования переменных. Выражение, описывающее эту суперпозицию, называли формулой. Поскольку понятие суперпозиции является очень важным в алгебре логики, рассмотрим его более подробно.

Пусть дано множество (конечное или бесконечное) исходных функций 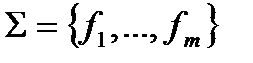. Символы переменных 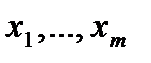, содержащихся в данных функциях, будем считать формулами глубины 0.

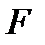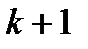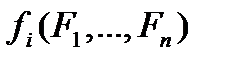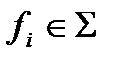Определение. Говорят, что формула имеет глубину , если она имеет вид , где , а 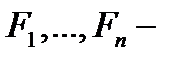формулы, максимальная из глубин которых равна 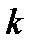. При этом 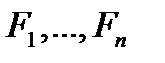называются подформулами формулы 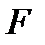, а 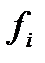называется внешней, или главной операцией формулы .

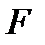Соответственно, формулы 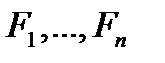также могут иметь подформулы, которые являются в этом случае и подформулами формулы 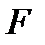. Например, выражение 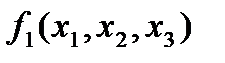в наших обозначениях – это формула глубины 1. Выражение 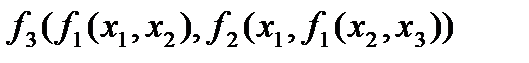является формулой глубины 3, содержащей одну подформулу глубины 2 и две подформулы глубины 1.

В дальнейшем конкретные формулы будем записывать в более привычном виде, при котором условные знаки функций стоят между аргументами (такую запись называют инфиксной). Например, если 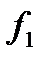является конъюнкцией, 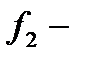дизъюнкцией, а 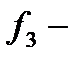импликацией, то приведённая выше формула примет вид .

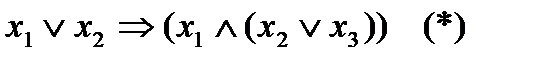Все формулы, построенные подобным образом, то есть содержащие только символы переменных, скобки и знаки функций из множества 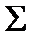, называются формулами над множеством .

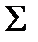Возможны и другие интерпретации понятия глубины. Например, считается, что расстановка отрицаний над переменными не увеличивает глубины формулы. В случае, когда множество 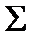содержит некоторую ассоциативную операцию 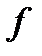, можно считать, что применение этой операции к формулам с той же внешней операцией 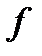не увеличивает глубины формулы. Например, формулы 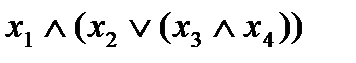и 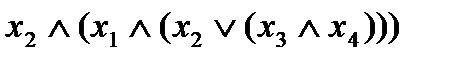имеют одну и ту же глубину 3.

Всякая формула, выражающая данную функцию, как суперпозицию других функций, задаёт способ её вычисления (при условии, что известно, как вычислять исходные функции). Этот способ определяется следующим очевидным правилом: формулу можно вычислить, только если уже вычислены значения всех её подформул. Применим, например формулу к набору 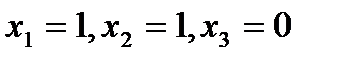. Получим: 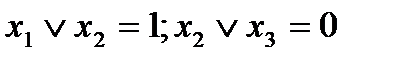. Далее получим 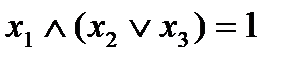. Наконец, .

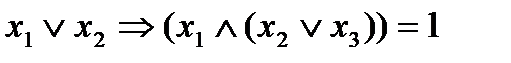Таким образом, формула ставит в соответствие каждому набору значений аргументов значение функции и, значит, может наряду с таблицей служить способом задания и вычисления функции. В частности, по формуле, вычисляя её на всех 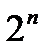наборах, можно восстановить таблицу функции. О формуле, задающей функцию, говорят также, что она представляет или реализует функцию.

В отличие от табличного задания представление данной функции формулой не единственно. Например, если в качестве исходного множества функций зафиксировать функции 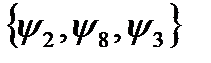из предыдущего пункта (то есть функции И, ИЛИ, НЕ), то функцию 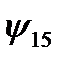- штрих Шеффера – можно представить формулам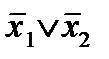и и 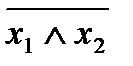. Функцию 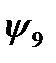- стрелка Пирса – можно представить формулам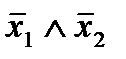и и .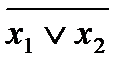

Определение. Формулы, представляющие одну и ту же функцию называются эквивалентными или равносильными.

Эквивалентность формул принято обозначать знаком равенства, поэтому можно записать: .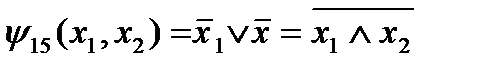

Существует стандартный метод для выяснения эквивалентности двух формул. По каждой формуле восстанавливается таблица функции, а затем две полученные таблицы сравниваются. Таким способом в предыдущеё лекции мы устанавливали равносильность высказываний. Он весьма громоздок, так как требует 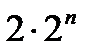вычислений, если считать, что обе формулы зависят от 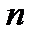переменных. Более простыми методами, позволяющими устанавливать эквивалентность данных формул, а также получать новые формулы, эквивалентные исходной, являются эквивалентные преобразования, которые будут рассмотрены в дальнейшем.