Лекция № 11. Полнота и замкнутость.

Ранее нами рассматривались два способа задания логических функций – табличный и с помощью формул. Таблица задаёт функцию непосредственно как соответствие между двоичными наборами и значениями функции на этих наборах. Этот способ универсален, то есть, пригоден для любых функций, однако слишком громоздок. Формула – гораздо более компактный способ задания функции, но она задаёт функцию через другие функции. Поэтому для любой системы функций 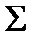возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В позапрошлой лекции был получен положительный ответ для системы 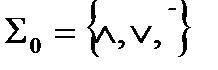(теорема 8.2). В данной лекции будет показано, как решать этот вопрос для произвольной системы .

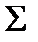1. Функционально полные системы.

Определение. Система функций 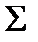называется функционально полной системой, если любая логическая функция может быть представлена формулой над системой 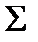(является суперпозицией функций этой системы).

Из теоремы 8.2 следует, что система 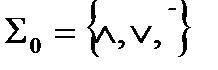является функционально полной. Равным образом, функционально полна любая система 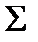, через функции которой можно выразить конъюнкцию, дизъюнкцию и отрицание. Действительно, для любой логической функции 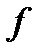из такой системы следует составить булеву формулу (а она обязательно существует согласно теореме 8.2) и потом выразить в ней конъюнкцию, дизъюнкцию и отрицание через функции системы 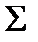. Аналогично обосновывается более общее утверждение.

Теорема 11.1. Если все функции функционально полной системы 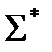представимы формулами над системой 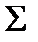, то система 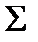также функционально полна.

Пример 1.

а) Системы 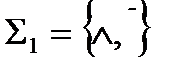и 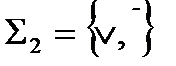функционально полны. Действительно, с помощью законов Де Моргана и двойного отрицания можно выразить в каждой из этих систем функцию, недостающую до через остальные две:

.

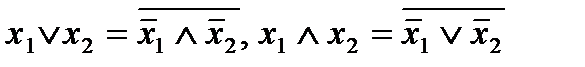С точки зрения функциональной полноты систему 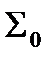следует считать избыточной: она сохраняет свойство полноты и при удалении из неё конъюнкции или дизъюнкции. Однако легко видеть из приведённого примера, что, хотя системы 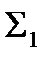и 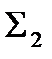не являются избыточными, зато формулы в них получаются гораздо длиннее: замена одной операции на другую вносит в формулу сразу три лишних отрицания.

б) Системы 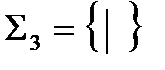(штрих Шеффера) и 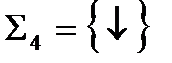(стрелка Пирса) являются функционально полными.

.

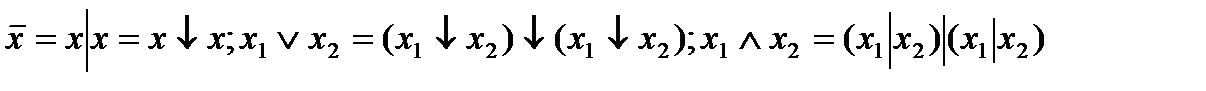Таким образом, система 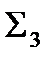сводится к системе 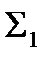, а система 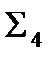- к системе .

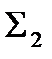в) Система 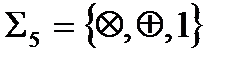( 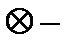умножение по модулю 2, 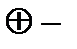сложение по модулю 2 – см. пункт 1 лекции № 8)) является функционально полной. Поскольку 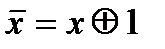, данная система сводится к .

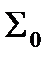На свойствах этой системы остановимся подробнее.

1. Алгебра Жегалкина и линейные функции.

Определение. Алгебра над множеством логических функций с двумя бинарными операциями 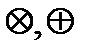называется алгеброй Жегалкина.

Замечание. Операция вполне аналогична операции конъюнкции (логического умножения). Однако операция имеет совершенно другой математический смысл, чем дизъюнкция (соответствующая функция ранее была названа неравнозначностью). Поэтому никак нельзя считать алгебру Жегалкина иной формой записи булевой алгебры.

В алгебре Жегалкина выполняются следующие соотношения (знак умножения опущен):

2.1. ,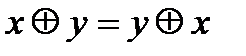

2.2. ,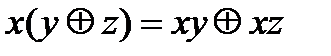

2.3 ,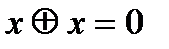

2.4 .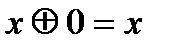

Кроме того, выполняются соотношения, ранее сформулированные булевой алгебры, относящиеся к конъюнкции и константам. Отрицание и дизъюнкция выражаются так:

2.5 ,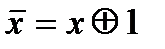

2.6 .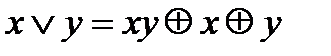

Если в произвольной формуле алгебры Жегалкина раскрыть скобки и произвести все упрощения по вышеуказанным соотношениям, то получится формула, имеющая вид Суммы произведений, то есть полином (многочлен) по модулю 2. Такая формула называется полиномом Жегалкина для данной функции.

От булевой формулы всегда можно перейти к формуле алгебры Жегалкина, используя равенства 2.5 и 2.6, а также прямое следствие из равенства 2.6: если 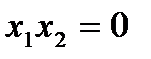, то 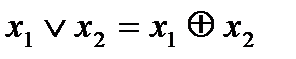. Оно, в частности, позволяет заменять знак дизъюнкции знаком в случаях, когда исходная формула представляет собой СДНФ.

Пример 2. Составить полиномы Жегалкина для данных функций:

а) ,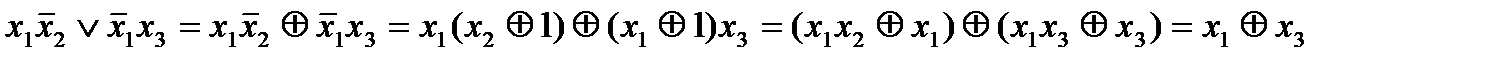

б) .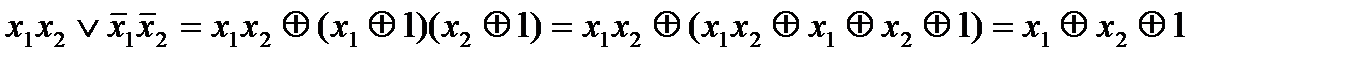

Заметим, что если в полученных полиномах Жегалкина произвести обратную замену функций, то получим упрощённые формулы булевой алгебры.

Теорема 11.2. Для всякой логической функции существует полином Жегалкина и притом единственный.

Существование такого полинома, по сути, уже доказано, а для доказательства его единственности достаточно показать существование взаимно однозначного соответствия между множеством всех функций 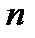переменных и множеством всех полиномов Жегалкина.

Определение. Функция, у которой полином Жегалкина имеет вид 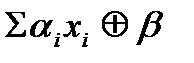, где параметры 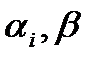равны нулю или единице, называется линейной.

Все функции от одной переменной линейны. Также линейными являются функции эквивалентность и сумма по модулю 2.

1. Замкнутые классы. Монотонные функции.

Определение. Множество 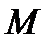логических функций называется замкнутым классом, если любая суперпозиция функций из множества 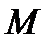снова принадлежит .

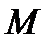Всякая система 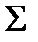логических функций порождает некоторый замкнутый класс, а именно класс всех функций, которые можно получить суперпозициями функций 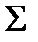. Такой класс называется замыканием 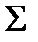и обозначается 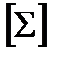. Если множество 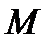- функционально полная система, то .

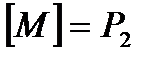Пример 3.

а) Множество всех дизъюнкций, то есть функций вида 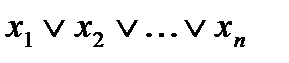является замкнутым классом.

б) Множество всех линейных функций является замкнутым классом, так как подстановка формул вида 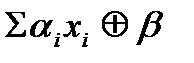после преобразований даёт формулу такого же вида.

Важнейшим примером замкнутого класса является класс монотонных функций, который будет рассмотрен далее.

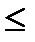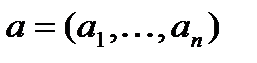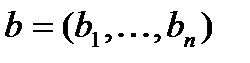Ранее рассматривалось отношение частичного порядка на множестве векторов одинаковой длины. Напомним, что для векторов и выполняется 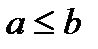, если для любого 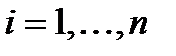выполняется 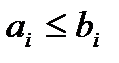. Здесь воспользуемся этим отношением для двоичных векторов.

Определение. Функция 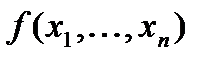называется монотонной, если для любых двух двоичных наборов длины 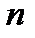из того, что 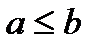следует .

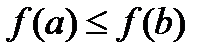Пример 4.

а) Функция 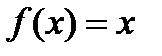монотонна.

б) Дизъюнкция и конъюнкция любого числа переменных являются монотонными функциями.

в) Рассмотрим две функции от трёх переменных, заданных следующей таблицей.

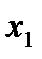
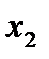
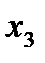
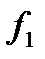
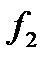
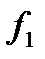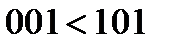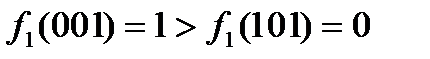Функция , очевидно, не является монотонной, так как, например , а . Монотонность функции 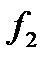легко установить непосредственной проверкой.

Проверка монотонности функции непосредственно по определению требует анализа таблицы функции и может оказаться достаточно трудоёмкой. Поэтому весьма полезной для установления монотонности является следующая теорема. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний.

Теорема 11.3. Всякая булева формула, не содержащая отрицаний, представляет собой монотонную функцию отличную от константы; наоборот, для любой монотонной функции, отличной от 0 и 1, найдётся представляющая её булева формула без отрицаний.

Из данной теоремы и того очевидного факта, что подстановка нескольких формул без отрицаний в формулу без отрицаний снова даёт формулу без отрицаний, вытекает следующая теорема.

Теорема 11.4. Множество всех монотонных функций является замкнутым классом.

Но поскольку всякая булева формула без отрицаний является суперпозицией дизъюнкций и конъюнкций, из данной теоремы непосредственно получаем следствие.

Следствие. Класс монотонных функций является замыканием системы функций .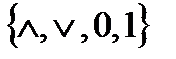

1. Теоремы о функциональной полноте.

Теперь перейдём к рассмотрению основного вопроса, поставленного в рамках данной лекции: каковы необходимые и достаточные условия функциональной полноты для произвольной системы функций 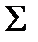? Вначале было сказано, что система 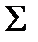полна, если конъюнкция, дизъюнкция и отрицание являются суперпозициями функций из системы 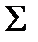. Поэтому будем искать свойства функций, позволяющие выразить через них булевы операции. Сначала сформулируем две леммы, позволяющие вывести соответствующие теоремы.

Лемма 1 (о немонотонных функциях). Если функция 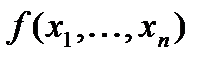немонотонна, то подстановкой констант из неё можно получить отрицание.

Практически данная лемма является утверждением, противоположным теореме, обратной к теореме 11.3. Смысл её заключается в том, что для функции 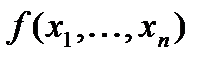существует такая подстановка 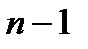константы, что функция оставшейся одной переменной является отрицанием.

Лемма 2 (о нелинейных функциях). Если функция 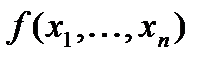нелинейна, то с помощью подстановки констант и использования отрицаний из неё можно получить дизъюнкцию или конъюнкцию.

Иначе говоря, существует представление дизъюнкции и конъюнкции в виде суперпозиции констант, отрицаний и нелинейной функции .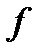

Замечание. При традиционных обозначениях переменных в выражениях вида 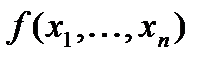, где переменные расположены в естественном порядке индексов, эти индексы играют двоякую роль: они именуют переменные и нумеруют их места в функции. Эти роли следует различать.

Две указанные леммы позволяют получить все булевы операции с помощью немонотонных функций, нелинейных функций и констант. Это ещё не полнота в точном смысле слова, так как константы с самого начала предполагались данными. Однако такое предположение часто бывает оправданным в различных приложениях (прежде всего в синтезе логических схем). Поэтому есть смысл ввести ослабленное определение полноты.

Определение. Система функций 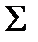называется функционально полной в слабом смысле, если любая логическая функция может быть представлена формулой над системой 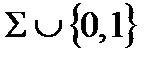, то есть является суперпозицией констант и функций из системы .

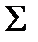Очевидно, что из обычной полноты системы следует её слабая полнота.

Теорема 11.5 (первая теорема о функциональной полноте). Для того, чтобы система функций 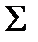была функционально полной в слабом смысле, необходимо и достаточно, чтобы она содержала хот бы одну немонотонную функцию и хотя бы одну нелинейную функцию.

Доказательство:

1) Необходимость. Классы монотонных и линейных функций замкнуты и содержат 0 и 1. Поэтому если 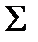не содержит немонотонных или нелинейных функций, то их нельзя получить с помощью суперпозиций функций из системы 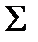и констант.

2) Достаточность. Пусть 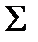содержит немонотонную и нелинейную функцию. Тогда по лемме 1 подстановкой констант из монотонной функции получаем отрицание, а затем по лемме 2 из нелинейной функции с помощью отрицаний и констант получаем дизъюнкцию и конъюнкцию.

Пример 5.

а) Система 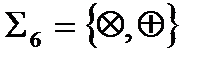функционально полна в слабом смысле, так как операция нелинейна (как и конъюнкция), а операция (сложение по 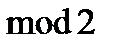) немонотонна.

б) В функционально полной системе 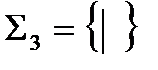единственная функция – штрих Шеффера – нелинейна и немонотонна.

Для формулировки необходимых и достаточных условий “cильной” полноты (в отличие от слабой) нужно ввести ряд определений, описывающих ещё три замкнутых класса функций.

Определение. Функция 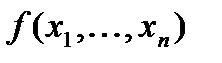называется сохраняющей ноль, если выполняется 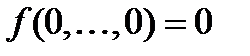и сохраняющей единицу, если выполняется .

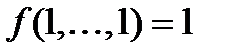Оба данных класса функций являются замкнутыми, что проверяется подстановкой констант в суперпозиции. Равным образом замкнутый класс образуют самодвойственные функции (такие, что ).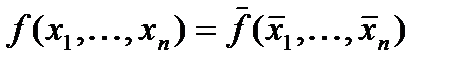

Теорема 11.6 (вторая – основная – теорема о функциональной полноте). Для того чтобы система функций 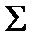была функционально полной (в сильном смысле), необходимо и достаточно, чтобы она содержала: 1) нелинейную функцию, 2) немонотонную функцию, 3) функцию, не являющуюся самодвойственной, 4) функцию, не сохраняющую ноль, 5) функцию, не сохраняющую единицу.