Лекция № 7. Элементы математической логики.
Математическая логика – разновидность формальной логики, т.е. науки, которая изучает умозаключения с точки зрения их формального строения.
Определение. Высказыванием называется предложение, к которому возможно применить понятия истинно или ложно.
В математической логике не рассматривается сам смысл высказываний, определяется только его истинность или ложность, что принято обозначать соответственно И или Л.
Понятно, что истинные и ложные высказывания образуют соответствующие множества. С помощью простых высказываний можно составлять более сложные, соединяя простые высказывания союзами “и”, “или”.
Таким образом, операции с высказываниями можно описывать с помощью некоторого математического аппарата.
Вводятся следующие логические операции (связки) над высказываниями
1) Отрицание. Отрицанием (логическим “не”) высказывания Р называется высказывание, которое истинно только тогда, когда высказывание Р ложно.
Обозначается  Р или
Р или 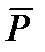 .
.
Соответствие между высказываниями определяется таблицами истинности. В нашем случае эта таблица имеет вид:
| P |  Р Р
|
| И | Л |
| Л | И |
2) Конъюнкция. Конъюнкцией (логическим “и”) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинны оба высказывания.
Обозначается P&Q или РÙQ.
| P | Q | P&Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | Л |
3) Дизъюнкция. Дизъюнкцией (логическим “или”) двух высказываний P и Q называется высказывание, ложное тогда и только тогда, когда оба высказывания ложны.
Обозначается PÚQ.
| P | Q | PÚQ |
| И | И | И |
| И | Л | И |
| Л | И | И |
| Л | Л | Л |
4) Импликация. Импликацией (логическим следованием) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда высказывание Р истинно, а Q – ложно.
Обозначается PÉQ (или РÞQ). Высказывание Р называется посылкой импликации, а высказывание Q – следствием.
| P | Q | PÞQ |
| И | И | И |
| И | Л | Л |
| Л | И | И |
| Л | Л | И |
5) Эквиваленция. Эквиваленцией (логической равносильностью) двух высказываний P и Q называется высказывание, истинное тогда и только тогда, когда истинности высказываний совпадают.
Обозначается Р~Q или РÛQ.
| P | Q | P~Q |
| И | И | И |
| И | Л | Л |
| Л | И | Л |
| Л | Л | И |
С помощью этих основных таблиц истинности можно составлять таблицы истинности сложных формул.
Замечание. В дальнейшем мы познакомимся с принципиально иной, более широкой трактовкой тех понятий, которые мы определили в данной лекции. Мы будем их рассматривать уже не как операции над высказываниями, но как некоторые функции. Поясним на следующем примере. Запись 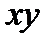 можно рассматривать как обозначение бинарной операции умножения переменных
можно рассматривать как обозначение бинарной операции умножения переменных 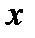 и
и 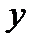 , а, с другой стороны, так же обозначается функция двух переменных
, а, с другой стороны, так же обозначается функция двух переменных 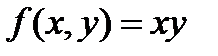 .
.
Пример 1. С помощью таблиц истинности проверить, являются ли эквивалентными формулы j и y.

Составим таблицы истинности для каждой формулы:
| p | r | 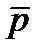
| (pÙr) | 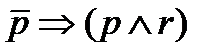
|
| И | И | Л | И | И |
| И | Л | Л | Л | И |
| Л | И | И | Л | Л |
| Л | Л | И | Л | Л |
| p | r | 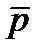
| 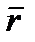
| 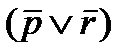
| 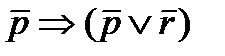
|
| И | И | Л | Л | Л | И |
| И | Л | Л | И | И | И |
| Л | И | И | Л | И | И |
| Л | Л | И | И | И | И |
Данные формулы не являются эквивалентными.
Пример 2. С помощью таблиц истинности проверить, являются ли эквивалентными формулы j и y.
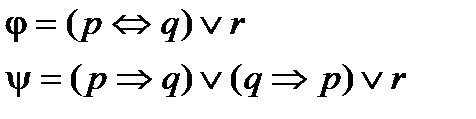
Составим таблицы истинности для заданных формул.
| p | q | r | pÛq | (pÛq)Úr |
| И | И | И | И | И |
| И | И | Л | И | И |
| И | Л | И | Л | И |
| И | Л | Л | Л | Л |
| Л | И | И | Л | И |
| Л | И | Л | Л | Л |
| Л | Л | И | И | И |
| Л | Л | Л | И | И |
| p | q | r | pÞq | qÞp | (pÞq)Ú(qÞp) | (pÞq)Ú(qÞp)Úr |
| И | И | И | И | И | И | И |
| И | И | Л | И | И | И | И |
| И | Л | И | Л | И | И | И |
| И | Л | Л | Л | И | И | И |
| Л | И | И | И | Л | И | И |
| Л | И | Л | И | Л | И | И |
| Л | Л | И | И | И | И | И |
| Л | Л | Л | И | И | И | И |
Из составленных таблиц видно, что данные формулы не равносильны.
Основные равносильности.
Для любых формул А, В и С справедливы следующие равносильности:
A & B º B & A; A & A º A; A & (B & C) º (A & B) & C;
A Ú B º B Ú A; A Ú A º A; A Ú (B Ú C) º (A Ú B) Ú C;
A Ú (B & C) º (A Ú B) & (A Ú C); A & (B Ú C) º (A & B) Ú (A & C);
A & (A Ú B) º A; A Ú (A & B) º A; ØØA º A; Ø(A & B) º ØA Ú ØB;
A º (A & B) Ú (A & ØB); A º (A Ú B) & (A Ú ØB);
Булевы функции.
Определение. Булевой функциейf(X1, X2, …, Xn) называется произвольная n – местная функция, аргументы и значения которой принадлежат множеству {0, 1}.
Вообще говоря, между логическими высказываниями, логическими связками и булевыми функциями просматривается явная аналогия (подробнее она рассматривается в следующей лекции). Если логические функции могут принимать значения истинно или ложно, то для булевой функции аналогами этих значений будут значения 0 или 1.
Для булевых функций также можно составить таблицы значений, соответствующим основным логическим операциям.
| X1 | X2 | ØX1 | X1&X2 | X1ÚX2 | X1ÞX2 | X1ÛX2 |
Дата добавления: 2016-06-05; просмотров: 2984;











