Распространения ударной волны
Рассмотрим гидравлический удар в трубопроводе при внезапном (мгновенном) закрытии задвижки в конце трубопровода с учетом реальных условий движения жидкости, а именно: жидкость сжимаема, а стенки трубопровода обладают упругими свойствами.
За бесконечно малый промежуток времени 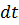 после закрытия задвижки движение жидкости прекращается на расстоянии
после закрытия задвижки движение жидкости прекращается на расстоянии 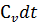 от задвижки. На этом бесконечно малом участке трубопровода произойдет повышение давления на величину
от задвижки. На этом бесконечно малом участке трубопровода произойдет повышение давления на величину 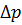 (рис.3.4).
(рис.3.4).
Определим величину 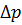 с помощью закона изменения количества движения.
с помощью закона изменения количества движения.
Рис.3.4
До закрытия задвижки количество движения в рассматриваемом объеме:
 , (3.1)
, (3.1)
где 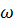 – площадь сечения трубы;
– площадь сечения трубы;
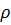 – плотность жидкости;
– плотность жидкости;
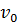 – скорость движения жидкости;
– скорость движения жидкости;
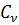 – скорость распространения ударной волны.
– скорость распространения ударной волны.
После закрытия задвижки скорость и количество движения уменьшились до нуля, т.е. в этом случае изменение количества движения стало равно начальному количеству движения.
Это изменение количества движения должно быть равно импульсу действующих сил.
Учитывая, что давление в сечении 1-1 равно 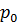 , а в сечении 2-2 повысилось до
, а в сечении 2-2 повысилось до 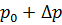 , находим импульс действующих сил в виде
, находим импульс действующих сил в виде
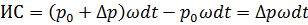 (3.2)
(3.2)
Запишем закон изменения количества движения с учетом выражений (3.1) и (3.2):
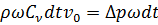 .
.
Отсюда
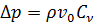 . (3.3)
. (3.3)
Формула (3.3) получена Н.Е.Жуковским и позволяет определить повышение давления при прямом гидравлическом ударе при известной скорости распространения ударной волны 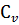 .
.
При абсолютно жестких стенках трубопровода скорость распространения ударной волны 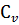 равна скорости распространения звука в воде
равна скорости распространения звука в воде 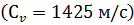 .
.
Определим скорость распространения ударной волны с учетом деформации стенок трубопровода и упругих свойств жидкости из условия сохранения массы жидкости при гидравлическом ударе.
До удара между сечениями 1-1 и 2-2 масса жидкости
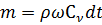 . (3.4)
. (3.4)
За время 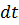 после закрытия задвижки в результате некоторого сжатия жидкости (т.е. увеличения ее плотности) и расширения трубы между сечениями 1-1 и 2-2 накопилась масса
после закрытия задвижки в результате некоторого сжатия жидкости (т.е. увеличения ее плотности) и расширения трубы между сечениями 1-1 и 2-2 накопилась масса
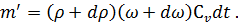 (3.5)
(3.5)
Накопленная масса образуется в трубопроводе в конце первой фазы в объеме 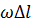 (см. рис.3.1):
(см. рис.3.1):
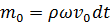 . (3.6)
. (3.6)
Условие сохранения массы при гидравлическом ударе с учетом выражений (3.4) – (3.3) и (3.6) запишется в виде 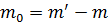 :
:
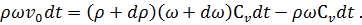 (3.7)
(3.7)
Сокращая выражение (3.7) на 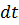 и пренебрегая бесконечно малыми величинами второго порядка, получим
и пренебрегая бесконечно малыми величинами второго порядка, получим
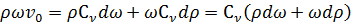 . (3.8)
. (3.8)
Выражение (3.8) является законом сохранения массы при гидравлическим ударе, из которого находим скорость 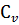 в виде:
в виде:
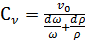 . (3.9)
. (3.9)
Из выражения (3.9) видно, что скорость ударной волны зависит от деформации трубы 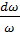 и сжатия
и сжатия 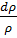 , которые характеризуются упругими свойствами материала трубы и жидкости.
, которые характеризуются упругими свойствами материала трубы и жидкости.
Представим выражение для относительной деформации площади трубы в виде
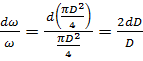 . (3.10)
. (3.10)
Из механики упругих тел известно, что относительная деформация 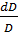 может быть выражена в зависимости от вызываемого ею растягивающего напряжения в материале трубы
может быть выражена в зависимости от вызываемого ею растягивающего напряжения в материале трубы 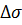 и модуля его упругости
и модуля его упругости 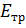 по закону Гука:
по закону Гука:
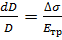 . (3.11)
. (3.11)
Напряжение, вызванное ударной волной в стенках трубы, может быть определено по формуле
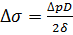 , (3.12)
, (3.12)
где 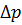 – давление в гидравлическом ударе;
– давление в гидравлическом ударе;
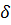 – толщина стенки трубы;
– толщина стенки трубы;
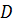 –диаметр трубы.
–диаметр трубы.
С учетом зависимостей (3.11) и (3.12) выражение (3.10) приводится к виду:
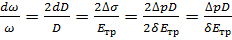 . (3.13)
. (3.13)
Относительное изменение плотности жидкости 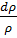 зависит от повышения давления
зависит от повышения давления 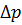 и модуля объемной упругости жидкости
и модуля объемной упругости жидкости 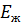 :
:
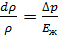 . (3.14)
. (3.14)
Подставим выражения (3.13) и (3.14) в формулу (3.9) и получим
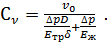 (3.15)
(3.15)
Рассмотрим физический смысл величин, находящихся под корнем в правой части формулы (3.15).
Если гидравлический удар, происходящий в трубе из абсолютно неупругого материала 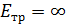 , то
, то
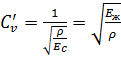 , (3.16)
, (3.16)
где 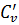 - скорость распространения упругих деформаций (ударной волны) в жидкости, м/с.
- скорость распространения упругих деформаций (ударной волны) в жидкости, м/с.
Из физики известно, что выражение 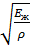 является скоростью звука в жидкой среде.
является скоростью звука в жидкой среде.
Для воды 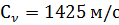 .
.
В другом предельном случае при 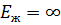 можно считать, что гидравлический удар происходит в трубе, по которой движется абсолютно неупругая жидкость. Тогда:
можно считать, что гидравлический удар происходит в трубе, по которой движется абсолютно неупругая жидкость. Тогда:
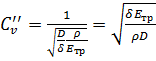 . (3.17)
. (3.17)
Можно также считать, что 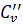 является скоростью распространения упругих деформаций (ударной волны) исключительно по телу трубы.
является скоростью распространения упругих деформаций (ударной волны) исключительно по телу трубы.
С учетом формул (3.16) и (3.17) преобразуем формулу (3.15) к виду:
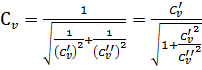 . (3.18)
. (3.18)
или
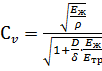 . (3.19)
. (3.19)
Учитывая, что 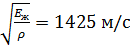 для воды, получим, м/с:
для воды, получим, м/с:
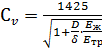 . (3.20)
. (3.20)
Подставим выражение (3.20) в формулу (3.3) и получим, Па:
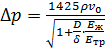 . (3.21)
. (3.21)
Отношение 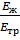 для воды в зависимости от материала стенки трубы принимается по табл.3.1.
для воды в зависимости от материала стенки трубы принимается по табл.3.1.
Таблица 3.1
| Вид труб | 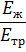
|
| Стальные | 0,01 |
| Чугунные | 0,02 |
| Асбестоцементные | 0,11 |
| Полиэтиленовые | 1…1,45 |
| Бетонные | 0,10…0,14 |
| Резиновые | 333…1000 |
Для железобетонных труб с учетом их армирования
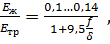 (3.22)
(3.22)
где 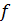 – площадь сечения кольцевой арматуры на 1 м длины стенки трубы.
– площадь сечения кольцевой арматуры на 1 м длины стенки трубы.
Обычно 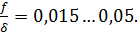
Дата добавления: 2016-06-05; просмотров: 3997;











