Множественная корреляция

Изменение экономических явлений происходит под влиянием не одного, а большого числа различных факторов. Для измерения тесноты корреляционной связи между результативным признаком и несколькими факторными признаками при линейной форме связи рассчитывается коэффициент множественной корреляции.

Коэффициент множественной корреляции, для случая двух факторных признаков x₁ и x₂ рассчитывается по формуле:

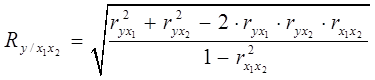(7.19)

Множественный коэффициент корреляции изменяется в пределах [0;1] и численно не может быть меньше, чем любой из образующих его парных коэффициентов. Приближение R к единице свидетельствует о сильной зависимости между признаками.

Средняя квадратическая ошибка коэффициента множественной корреляции определяется по формуле:

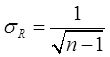(7.20)

Тогда, если 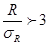, то с вероятностью близкой к 0,99 можно считать коэффициент множественной корреляции значимым.

Проверка значимости коэффициента множественной корреляции осуществляется так же по F-критерию Фишера. Для случая двух факторных признаков х₁ и х₂ он имеет вид:

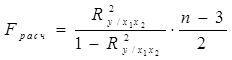(7.21)

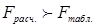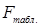Коэффициент множественной корреляции считается статистически значимым, если _, где находится по таблице распределения Фишера с параметрами .

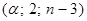В ходе изучения множественной корреляции рассчитывают также частные коэффициенты корреляции. Частные коэффициенты корреляции характеризуют степень тесноты связи между двумя признаками при фиксированном значении всех остальных. Для случая двух факторных признаков x₁ и x₂ формулы будут иметь вид:

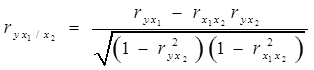(7.22)

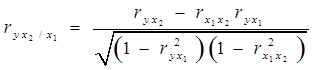(7.23)

В первом случае исключено влияние факторного признака х₂, а во втором х₁. Значения парного и частного коэффициентов корреляции отличаются друг от друга, т.к. парный коэффициент характеризует связь между двумя признаками без учета влияния других признаков, а частный учитывает наличие и влияние других факторов.

Проверка значимости и расчет доверительных интервалов для частных коэффициентов корреляции аналогичны, как и для парных коэффициентов корреляции, с тем лишь отличием. Что число степеней свободы n определяется так: n = n - k., где k – порядок коэффициента частной корреляции.

7.2. Контрольные вопросы к теме 7

1.Какие типы взаимосвязей между явлениями Вы знаете?

2.В чем сущность корреляционной связи между явлениями

3.Что такое «ложная» корреляция?

4.Охарактеризуйте корреляционные связи по направлению и по аналитическому выражению.

5.Какие методы применяют в начальной стадии анализа статистических зависимостей?

6.Какие существуют показатели измерения тесноты связи?

7.Как оценивается значимость коэффициента корреляции, рассчитанного по выборочным данным?

8.Что представляют собой коэффициенты рангов Спирмена и Кендэлла?

9.С помощью каких показателей изучается и измеряется корреляционная зависимость между качественными показателями на основе таблиц взаимной сопряженности?

10.Определите понятие множественной корреляции.

11.Что такое совокупный и частные коэффициенты корреляции? В чем их отличие?