Оценка качества псевдослучайных чисел

Результаты имитационного моделирования, как показывает практика, существенно зависят от качества используемых последовательностей псевдослучайных чисел.

Поэтому применяемые в имитационной модели генераторы случайных чисел должны пройти тесты на пригодность.

Основными анализируемыми характеристиками генерируемых датчиком последовательностей являются:

- равномерность распределения;

- стохастичность (случайность);

- независимость.

Проверка равномерности.

Она может быть выполнена с помощью гистограммы относительных частот генерируемой случайной величины. Для ее построения интервал [0; 1] разбивается на mравных частей и подсчитывается относительное число попаданий значений случайной величины Y в каждый интервал (см. рисунок 6.2, где P* - частость появления величины в том или ином интервале).

Чем ближе огибающая гистограммы к прямой 1/m, тем в большей степени генерируемая последовательность отвечает требованиям равномерности.

Проверка стохастичности.

Для этого используется метод комбинаций. Суть метода заключается в следующем. Выбирают достаточно большую (длинную) последовательность случайных чисел x_i и для нее определяют вероятность появления в каждом из x_i ровноj единиц (“1”).

При этом могут анализироваться как все разряды числа, так и только (“l”) старших. Теоретически закон появления j единиц в lразрядах двоичного числа может быть описан как биноминальный закон распределения.

Тогда при длине выборки N ожидаемое число появлений случайных чисел x_i с j единицами в проверяемых l разрядахравно:

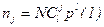, (6.3)

где 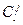- число комбинаций (сочетаний) j единиц в l разрядах;

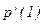- вероятность появления единицы в двоичном разряде, .

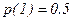Для полученной последовательности определяется эта же характеристика. Поверка соответствия реального значения характеристики теоретическому выполняется с помощью одного из статистических критериев согласия.

Проверка независимости.

Проводится на основе вычисления корреляционного момента.

Для независимых случайных величин корреляционный момент равен нулю.