Кинематический анализ механизма
5.4.1. Построение планов механизма
Определяем угол качения кулисы по заданному коэффициенту изменения скорости:
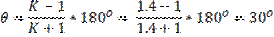
Определение длин звеньев:
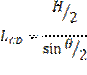
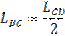
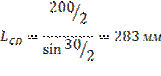
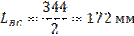
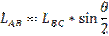
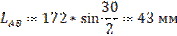
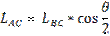
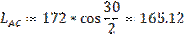
Вычисляем величину масштабного коэффициента:
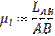
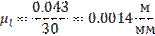
5.4.2. Построение планов скоростей
Рассчитываем угловую скорость кривошипа по формуле:
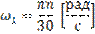
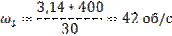
Найдем скорость ведущего звена группы (0; 1) B1 (VB1).
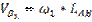
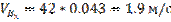
Изображаем скорость отрезка Pb1  равным по величине 110 мм, получаем величину масштабного коэффициента:
равным по величине 110 мм, получаем величину масштабного коэффициента:
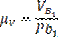
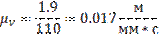
Выбираем полюс P. Отрезок Pb1 направлен перпендикулярно кривошипу в сторону его вращения. В группе (2; 3) определяем сначала скорость VB3, которая в данном положении механизма совпадает с точкой B1. Рассматривая движение точки B3 сначала по отношению к центру шарнира B1, запишем 2 векторных уравнения:
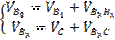
Скорость скольжения 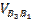 точки B3 кулисы 3 относительно центра B1 шарнира направлена перпендикулярно CB.
точки B3 кулисы 3 относительно центра B1 шарнира направлена перпендикулярно CB.
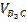 – относительная скорость точки B3 во вращательном движении точки звена 3 вокруг точки C. VC = 0, т. е. она неподвижна.
– относительная скорость точки B3 во вращательном движении точки звена 3 вокруг точки C. VC = 0, т. е. она неподвижна.
Из точки P проводим pd3 перпендикулярно звену CD. Из точки b1 проводим b1b3 параллельно звену CD. pd3 является абсолютной скоростью кулисы B3.
Длину отрезка pd3 найдем из соотношения:
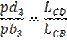
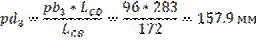
Зная длину отрезка pd3 = 157.9 мм, в группе Ассура (4-5) определяем скорость точки E5. Запишем векторное уравнение скорости для точки E5.
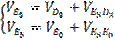
Скорость выходного звена E5 находится графически, путем пересечения двух векторов из точки P проводим отрезок Pe5, параллельно оси X-X. Из точки d3 проводим d3e5 перпендикулярно звену 5. Используя план скоростей, находим отрезки векторов скоростей:
Pb1 = 110 мм;
Pb3 = 102 мм;
Pd3 = 157.9 мм;
Pe5 = 155 мм;
d3e5 = 23 мм;
b1b3 = 40 мм.
Определяем действительные скорости:
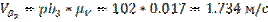
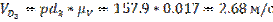
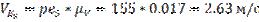
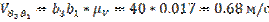
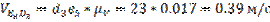
5.4.3. Построение плана ускорений
Ускорение точек механизма находится в соответствии с последовательностью образующих звеньев в механизме.
Для механизма I класса ускорение центра шарнира B:
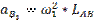
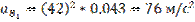
Так как угловая скорость 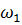 = const, то касательное ускорение B по отношению к центру точки A будет равно нулю.
= const, то касательное ускорение B по отношению к центру точки A будет равно нулю.
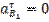
На чертеже выбираем полюсную точку П. Откладываем из точки П отрезок Pb=150 мм, параллельно звену AB и в направлении от точки B к точке A.
Определяем величину масштабного коэффициента:
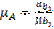
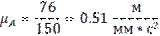
Определим сначала ускорение 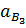 точки B3 кулисы 3, совпадающей в данном положении механизма с центром шарнира B1. Рассматривая звенья точки B3 кулисы сначала по отношению к центру шарнира B1, а затем по отношению к центру вращения кулисы, запишем 2 векторных уравнения:
точки B3 кулисы 3, совпадающей в данном положении механизма с центром шарнира B1. Рассматривая звенья точки B3 кулисы сначала по отношению к центру шарнира B1, а затем по отношению к центру вращения кулисы, запишем 2 векторных уравнения:
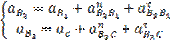
Из этого уравнения определим Кориолисово ускорение:
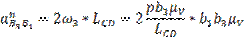
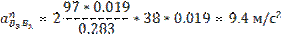
Вектор данного ускорения будет направлен в туже сторону, куда и направлен вектор скорости 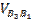 , если его повернуть на 90o против часовой стрелки.
, если его повернуть на 90o против часовой стрелки.
Кориолисово ускорение изображается отрезок b1k, длина которого равна:
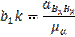
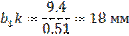
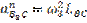
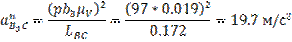
Изображаем отрезок Пn3 равным:
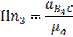
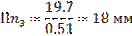
Вектор тангенциального ускорения точки B3 относительно точки C направлен перпендикулярно к отрезку BC.
Из конца вектора углового ускорения первого звена точки B1 перпендикулярно звену 3 проведем отрезок b1k и через точку k проведем прямую, параллельную BC. Затем из полюсной точки П откладываем отрезок Пn3 и через точку n3 проводим прямую перпендикулярную Пn3. На пересечении точек получаем точку b3 – конец вектора Пb3 – абсолютное ускорение 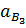 точки B3 кулисы. Соединив полюс П с точкой b3 получим отрезок Пb3 = 70 мм. На продолжении отрезка Пb3 определяем положение точки d3. Длину вектора d3найдем из соотношения:
точки B3 кулисы. Соединив полюс П с точкой b3 получим отрезок Пb3 = 70 мм. На продолжении отрезка Пb3 определяем положение точки d3. Длину вектора d3найдем из соотношения:
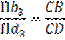
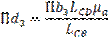
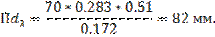
Определяем ускорение точки E5. Из положения точки П проводим отрезок Пe5 параллельно оси X-X. Из точки d3 проводим отрезок d3e5 перпендикулярный звену DE.
Определяем действительные ускорения:
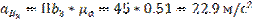
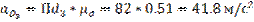
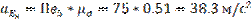
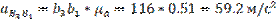
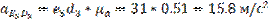
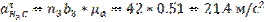
Определяем угловое ускорение:
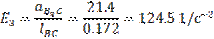
Дата добавления: 2021-12-14; просмотров: 390;











