Лабораторная работа №4 Измерение сопротивления методом амперметра и вольтметра.
Цель работы:
Изучить метод вольтметра-амперметра для измерения сопротивлений на постоянном токе.
Приобрести навыки в проведении измерений сопротивлений резисторов указанным методом,
Экспериментально проверить точность метода путём сопоставления результатов измерений с номинальными значениями сопротивлений резисторов.
Приобрести навыки количественной оценки точности результатов измерений и расчётов.
Краткая теория
Изучение сопротивлений на постоянном токе с помощью вольтметра и амперметра.
Эти измерения можно производить по двум схемам, показанным на рисунках
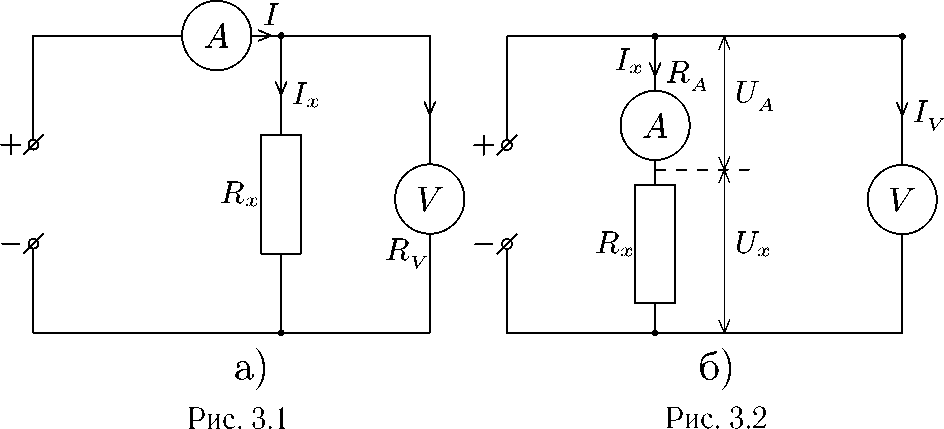
Ценность этих систем заключается в том, что по элементу электрической цепи, сопротивление которого измеряется, можно пропустить такой же ток, как и в условиях его работы, очень важно при измерениях сопротивлений, значения которых зависят от тока.
Идея косвенного измерения сопротивления амперметром и вольтметром основана на использовании закона Ома для участка цепи, не содержащей источника ЭДС, т.е. измеряемое сопротивление подсчитывается по величинам напряжения и тока:

где U и I показания вольтметра и амперметра. При этом получается лишь приближенное значение измеряемого сопротивления, т.к. в случае схемы а) амперметр измеряет суммарный ток исследуемого элемента цепи и вольтметра:
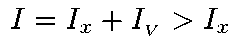 ,а в случае схемы б) вольтметр измеряет суммарное напряжение амперметра и исследуемого элемента цепи:
,а в случае схемы б) вольтметр измеряет суммарное напряжение амперметра и исследуемого элемента цепи:
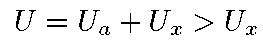 .
.
Действительное значение сопротивления Rx определяется так: для схемы а)
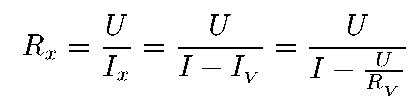
для схемы б) :
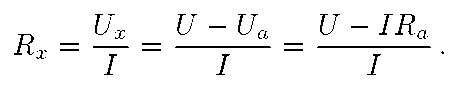
Как видно из выражений, при подсчёте величины искомого сопротивления по приближённой формуле, будет иметь место погрешность.
Так как в практике измерений сопротивлений этим методом подсчёт сопротивлений часто производят по приближённой формуле, то необходимо знать, какую схему следует выбрать для того, чтобы величина погрешности была невелика.
Рассмотрим выражения для относительных погрешностей обеих схем. Для схемы а) погрешность равна:
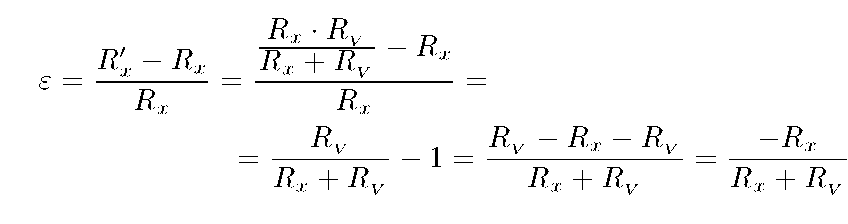
Замечание:
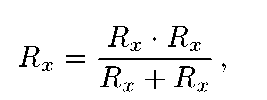 т.к. Rx и RV соединены параллельно.
т.к. Rx и RV соединены параллельно.
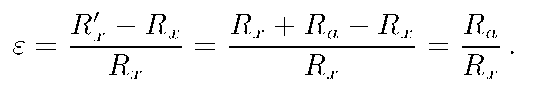
Для схемы б) относительная погрешность определяется выражением:
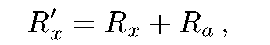 т.к. Rx и Ra соединены последовательно.
т.к. Rx и Ra соединены последовательно.
Из выражений вытекают следующие выводы:
схема а) при использовании приближённой формулы даёт заниженную величину измеряемого сопротивления по сравнению с его действительным значением. При этом погрешность тем меньше чем больше сопротивление вольтметра RV по сравнению с измеряемым сопротивлением. Поэтому пользоваться схемой а) следует в тех случаях, когда 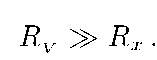
схема б) при расчёте по формуле (3.1) даёт завешенную величину измеряемого сопротивления по сравнению с его действительным значением. При этом погрешность тем меньше, чем меньше сопротивление амперметра Ra по сравнению с измеряемым сопротивлением. Поэтому пользоваться схемой б) следует в тех случаях когда 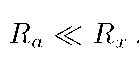
Именно поэтому в большинстве случаев практики схему а) рис. 3.1 применяют для измерений малых сопротивлений, а схему б) рис. 3.2 для измерения средних и больших сопротивлений.
Вместе с тем следует иметь в виду, что для любого значения Rx при определённом соотношении сопротивлений Rx, Ra и RV, схема включения приборов не влияет на величину погрешности. Это имеет место для такого значения Rx, при котором абсолютные значения погрешностей, вычисленные по формуле, равны между собой 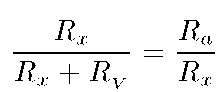
Из этого условия получаем
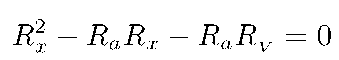
Решая это квадратное уравнение и пренебрегая величиной R2a по сравнению с 4RaRv и величиной Raf2 по сравнению с 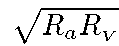 , что можно
, что можно
сделать ввиду малости сопротивления амперметра, найдём что
 Очевидно, что при соблюдении условия, выбор любой из двух схем включения приборов практически безразличен и произволен.
Очевидно, что при соблюдении условия, выбор любой из двух схем включения приборов практически безразличен и произволен.
Описание экспериментальной установки
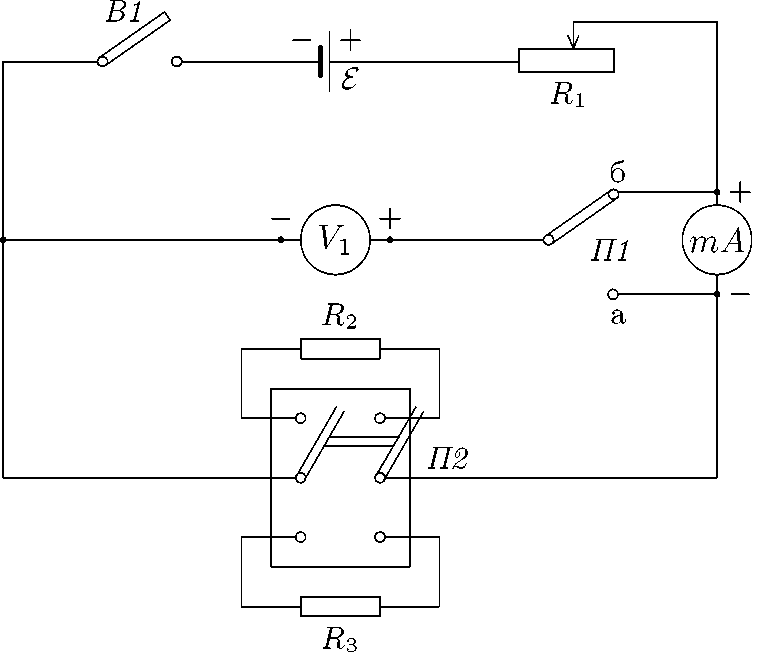 Принципиальная схема установки для измерения сопротивлений на постоянном токе вольтметром-амперметром
Принципиальная схема установки для измерения сопротивлений на постоянном токе вольтметром-амперметром
|
В состав экспериментальной установки входят:
источник постоянного тока с ЭДС E порядка 0, 5 B,
выключатель однополюсный B1 на источнике питания,
реостат ползунковый Ri на 500 Ом,
вольтметр,
переключатель однополюсной на два положения П1,
миллиамперметр,
переключатель двухполюсной на два положения П2,
резистор R2,
резистор R3.
Реостат R1 служит для регулирования силы тока в измерительной цепи.
Резисторы R2 и R3 являются субъектами, сопротивление которых подлежит измерению. Такую же роль выполняет и магазин сопротивлений.
Конструктивно резисторы R2 и R3 расположены на панели переключателя П1, который обеспечивает поочерёдное включение их в измерительную схему. При необходимости переключатель П2 с резисторами R2 и R3 заменяется магазином сопротивлений.
Переключатель П1 позволяет реализовать две возможные схемы измерения сопротивлений методом вольтметра-амперметра (см. схемы на рис. 3.1 и рис. 3.2).
Задание и порядок его выполнения
Собрать схему исследования
Составить перечень используемых электроизмерительных приборов в установке и записать их технические характеристики:
Таблица 1
| № п/п | Наименование приборов и его назначение в схеме | Заводской номер прибора | Система и тип прибора | Класс точности | Пределы измерения и цена деления | Абсо лютная погре шность | Сопро тивление прибора |
Рассчитать абсолютные погрешности измерительных приборов для используемых в работе пределов измерения, определить цену деления соответствующих шкал и занести их в таблицу 1.
Произвести однократные косвенные измерения сопротивлений резисторов R2 и R3 по схемам а) и б). Экспериментальные данные занести в таблицу 2.
Таблица 2
| Схема А | Схема Б | ||||||||
| R2 | R3 | R2 | R3 | ||||||
| U | I | U | I | U | I | U | I | ||
| В | mА | В | mА | В | mА | В | mА | В | mА |
Рассчитать величины измеренных сопротивлений резисторов по приближённой формуле и точным формулам для схем а) и б) соответственно. Определить погрешности косвенных измерений. Результаты расчётов занести в таблицу 3.
Таблица 3
| Схема | Резистор | Номинальное значение сопротивления резистора | Расчётное значение сопротивлений резисторов | |||||||
| Ri Ом |
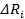 Ом Ом
| 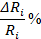
| по точной формуле | По приближённой формуле | ||||||
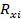 Ом
Ом
| 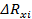 Ом
Ом
| 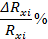
| 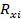
| 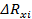
| 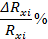
| |||||
| А | R2 | |||||||||
| R3 | ||||||||||
| Б | R2 | |||||||||
| R3 |
Дата добавления: 2021-12-14; просмотров: 727;











