Пример класса Matrix производного от базового класса Array

public class Matrix : Array

{

public Matrix()

{

m = 5;

n = 10;

matr = new Array[m];

for (int i = 0; i < m; i++)

matr[i] = new Array(n);

Console.WriteLine("Matrix без параметров выполнен.");

}

public Matrix(int m, int n)

{

this.m = m;

this.n = n;

matr = new Array[m];

for (int i = 0; i < m; i++)

matr[i] = new Array(n);

Random rnd = new Random();

for (int i = 0; i < m; i++)

for (int j = 0; j < n; j++)

matr[i].ar[j] = rnd.Next(100);

Console.WriteLine("Matrix с параметрами выполнен.");

}

public void PrintMatrix()

{

for (int i = 0; i < m; i++)

matr[i].PrintArray();

}

// Метод выполняет сортировку элементов строк матрицы по возрастанию

// с использованием метода вставки

public void SortMatrix()

{

int j,k,l,el;

for (int i = 0; i < m; i++)

for (j = 1; j < n; j++)

{

el = matr[i].ar[j];

k = 0;

while (el > matr[i].ar[k])

k++;

for (l = j - 1; l >= k; l--)

matr[i].ar[l + 1] = matr[i].ar[l];

matr[i].ar[k] = el;

}

}

public static bool operator ==(Array ar1, Array ar2)

{

int t1, t2;

t1 = t2 = 0;

for (int i = 0; i < ar1.n; i++)

{

if (ar1.ar[i] == 0)

++t1;

if (ar2.ar[i] == 0)

++t2;

}

return (t1 == t2);

}

public static bool operator !=(Array ar1, Array ar2)

{

return !(ar1 == ar2);

}

public override bool Equals(object obj)

{

try

{

return (bool)(this == (Array)obj);

}

catch

{

// Если obj не принадлежит классу Array

return false;

}

}

private int m;

private int n;

private Array[] matr;

}

// Конец определения производного класса Matrix

class Program

{

static void Main(string[] args)

{

Matrix m0 = new Matrix();

Console.WriteLine("\n");

Matrix m1 = new Matrix(5,10);

Console.WriteLine("\nИсходная матрица:");

m1.PrintMatrix();

m1.SortMatrix();

Console.WriteLine("\nОтсортированная матрица:");

m1.PrintMatrix();

Console.ReadKey();

}

}

Задание

1. Изучить понятие наследования классов, а также возможности языка программирования С# для работы с наследованием классов.

2. На основе класса Array, реализованного в лабораторной работе №8, и согласно индивидуальному заданию (табл. 12) создать производный от него класс Matrix.

3. Дочерний класс должен содержать такие закрытые члены:

- высота матрицы;

- ссылка на массив векторов базового класса;

а также следующие открытые методы:

- конструктор без параметров, создающий нулевую матрицу фиксированного размера; размер задается константами;

- конструктор с параметрами, создающий и инициализирующий матрицу случайных чисел в заданном диапазоне; размер задается с использованием параметров;

- метод вывода элементов матрицы на консоль;

- метод, реализующий вычисление заданного показателя P, для которого предусмотреть свойство в классе Matrix;

- метод, реализующий заданное преобразование матрицы посредством перегрузки заданного оператора;

- метод, реализующий заданную сортировку матрицы (нечетные варианты – по столбцам, четные варианты – по строкам).

Конструкторы должны выводить сообщение о своем срабатывании.

При программировании методов выполнять обработку необходимых исключений (ввод данных, работа с элементами массива, арифметика).

4. Составить тестовую программу, демонстрирующую реализацию указанных методов, в том числе обработку исключений.

5. Разработать блок-схему алгоритма метода Main.

Таблица 12. Варианты заданий к лабораторной работе №9

№ вар.	Массив и длина	Интервал генерации	Показатель Р	Алгоритм обработки	Перегружае­мый оператор	Метод сортировки
	А(10, 8)	[-10, 25]	Сумма произведений элементов строки и столбца матрицы, на пересечении которых находится наибольший по абсолютной величине элемент матрицы.	Все отрицательные элементы, расположенные по периметру матрицы заменить их абсолютными значениями.	Унарный +	Вставкой
	Х(5, 10)	[-15, 10]	Количество элементов матрицы, превышающих ее среднее арифметическое значение.	Все положительные элементы матрицы умножить на ее среднее арифметическое значение.	*	Обменом
	Y(10, 12)	[-20, 10]	Сумма элементов матрицы, для которых i+j=k, где k - введенное с клавиатуры зна­чение. Проверить, что значение k позволяет найти решение для каждой из матриц.	Все элементы матрицы, превышающие ее среднее арифметическое значение разделить на максимальный элемент.	/	Выбором
	Z(10, 7)	[-30, 40]	Сумма положительных элементов столбца, содержащего максимальный элемент матрицы.	Все элементы столбца, содержащего минимальный элемент матрицы, уменьшить на ее среднее арифметическое значение.	Унарный –	Быстрая (рекурсив­ная)
	В(6, 11)	[-20, 25]	Разность между максимальным и мини­мальным значениями элементов массива.	Все элементы строк, начинающихся с отрицательных элементов, умножить на максимальный элемент матрицы.	*	Шейкерная
	С(8, 12)	[-15, 75]	Сумма элементов, расположенных по периметру матрицы.	Столбцы матрицы упорядочить по возрастанию значений их элементов, минимальные элементы в столбцах увеличить на 1	++	Вставкой
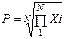
	А(10, 9)	[-30, 100]	Среднее геометрическое элементов матрицы:	Все элементы матрицы уменьшить на ее максимальное значение	Бинарный –	Обменом
	Х(9, 12)	[-40, 20]	Отношение среднего арифметического значения к минимальному элементу матрицы.	Строки матрицы упорядочить по убыванию значений их элементов, максимальные элементы в строках декрементировать	––	Выбором
	Y(10, 10)	[-50, 60]	Произведение ненулевых элементов строки матрицы, на которой расположен максимальный элемент.	Все элементы матрицы увеличить на ее среднее арифметическое значение.	Бинарный +	Быстрая (рекурсив­ная)
	Z(7, 9)	[-25, 15]	Сумма значений элементов матрицы, меньших ее среднего арифметического значения.	Все положительные элементы строки, содержащей максимальный элемент разделить на ее среднее арифметическое значение	/	Шейкерная
	T(5, 14)	[-10, 5]	Разность между суммой значений элементов четных и нечетных строк	Элементы строк, у которых минимальные элементы положительные, увеличить на значения этих элементов.	Бинарный +	Вставкой
	A(8, 8)	[-5, 10]	Отношение суммы ненулевых элементов к сумме положительных элементов матрицы	Элементы столбцов, у которых среднее арифметическое значение отрицательно, умножить на эти средние значения.	*	Обменом
	N(12, 6)	[-20, 10]	Абсолютное значение произведения ненулевых элементов, принадлежащих интервалу [-2, 2]	Все элементы матрицы, превышающие ее среднее арифметическое значение, возвести в степень P.	^	Выбором
	B(11, 11)	[-30, 0]	Количество отрицательных элементов матрицы	Все элементы столбца, содержащего минимальный элемент матрицы, уменьшить на ее среднее арифметическое значение.	Бинарный –	Быстрая (рекурсив­ная)
	M(10, 5)	[-20, 25]	Сумма элементов матрицы, больших ее среднего значения	Элементы столбцов матрицы циклически сдвинуть влево на число положительных элементов в в них	<<	Шейкерная
	R(5, 12)	[-15, 75]	Минимальный по абсолютной величине элемент матрицы	Все элементы строк, начинающихся с отрицательных элементов, умножить на максимальный элемент матрицы.	*	Вставкой
	C(10, 10)	[-30, 100]	Отношение сумм элементов, лежащих выше и ниже главной диагонали матрицы.	У элементов строк матрицы, начинающихся с положительных значений, сменить знак	Унарный –	Обменом
	F(7, 7)	[-40, 20]	Отношение произведения ненулевых элементов к сумме положительных элементов матрицы.	Транспонировать матрицу	!	Выбором
	S(10, 4)	[-40, 60]	Отношение максимального и минимального элементов матрицы	Все элементы матрицы уменьшить, меньше среднего арифметического, уменьшить на 1	––	Быстрая (рекурсив­ная)
	U(6, 15)	[-15, 15]	Сумма элементов столбца в котором расположен максимальный элемент матрицы.	Элементы строк, у которых минимальные элементы положительные, увеличить на 1	++	Шейкерная
	V(11, 5)	[-20, 5]	Разность модуля суммы отрицательных элементов и суммы положительных элементов	Все элементы матрицы увеличить на ее максимальное значение	Бинарный +	Вставкой
	D(9, 9)	[-15, 10]	Произведение ненулевых элементов, лежащих выше главной диагонали матрицы	Элементы столбцов, у которых среднее арифметическое значение отрицательно, умножить на эти средние значения.	*	Обменом
	L(5, 11)	[-20, 20]	Количество элементов матрицы, больших ее среднего значения.	Все положительные элементы строки, содержащей максимальный элемент разделить на ее среднее арифметическое значение.	/	Выбором
	G(8, 8)	[-30, 20]	Произведение элементов строк с положительными средними значениями для матрицы.	Элементы столбцов матрицы, у которых среднее арифметическое значение >0 упорядочить по возрастанию.	>	Быстрая (рекурсив­ная)
	K(6, 5)	[-10, 55]	Сумма элементов строк с нечетными индексами, не превышающих среднее значение по матрице	Элементы столбцов матрицы, у которых среднее арифметическое значение <0 упорядочить по убыванию	<	Шейкерная
	Q(7, 7)	[0, 99]	Число нулевых младших разрядов элементов матрицы	Логически сдвинуть элементы строк вправо на P позиций	>>	Вставкой
	Y(10, 10)	[-50, 60]	Максимальный из старших разрядов элементов, лежащих выше главной диагонали	Логически сдвинуть элементы столбцов влево на P позиций	<<	Обменом
	Z(7, 9)	[0, 12]	Число простых чисел в матрице	Возвести элементы строки, содержащей максимальный элемент, в степень P	^	Выбором
	T(5, 14)	[-10, 5]	Сумма разностей элементов столбцов с максимальным и минимальным по модулю элементами	Совпадающие столбцы матрицы обнулить	==	Быстрая (рекурсив­ная)
	A(8, 8)	[0, 10]	Разность сумм элементов главной и побочной диагоналей	Циклически сдвинуть элементы столбцов на P позиций	>>	Шейкерная

Содержание отчета

1. Титульный лист.

2. Цель работы, индивидуальное задание (таблица).

3. Листинг программы.

4. Блок-схему алгоритма метода Main().

5. Результаты тестирования всех методов.

6. Описание различий в работе конструкторов базового и производного классов.

7. Выводы.