Основные уравнения АД. Схема замещения

Потоки взаимоиндукции, создаваемые токами в фазах ста­тора создают основной или рабочий поток машины, как это было отмечено выше. Намагничивающие силы обмоток стато­ра и ротора создают так же и потоки рассеяния, обусловлива­ющие потокосцепления рассеяния ψ_1σ и ψ_2σ и индуктивности рассеяния L_1σ и L_2σ ­.

Основной вращающийся поток Ф, пересекая витки фаз обмотки статора, создает в каждой фазе синусоидальную ЭДС е_1,действующее значение которой определяется соотно­шением:

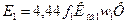(3.14)

Кроме того, этот поток, пересекая проводники обмотки ро­тора, создает в фазах (стержнях) ротора ЭДС е₂. Его действу­ющее значение:

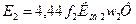. (3.15)

Если ротор заторможен (s=1 и f₂=f₁), то действующее значение ЭДС фазы ротора равно:

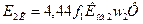или E₂ = E_2Ks.

Отношение ЭДС обмотки статора Е, к ЭДС ротора Е_2К при s = 1 называется коэффициентом трансформации машины или коэффициентом приведения ЭДС:

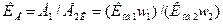, (3.16)

где К_об1 и К_об2— обмоточные коэффициенты, учитывающие влияние распределения обмотки фазы на величину намагни­чивающей силы обмотки. Умножая w₁на К_об1можно привести распределенную обмотку к эквивалентной сосредоточенной обмотке. Для обмотки статора К_об1 < 1. Для обмотки типа «беличья клетка» К_об = 1.

Рис. 3.9. Схема замещения для одной фазы статора и одной фазы

ротора асинхронного двигателя

Схема замещения трехфазного асинхронного двигателя для одной фазы, будет иметь вид, приведенный на рис. 3.9.

Для фазы обмотки статора можно записать уравнение Кирхгофа в виде:

Ū₁ = Ī₁R₁ +j Ī ₁X₁–Ē₁, (3.17)

где X₁= ω₁L_1σ— индуктивное сопротивление рассеяния фазы обмотки статора. Для фазы заторможенного ротора уравне­ние Кирхгофа имеет вид:

Ē_2К= Ī₂R₂+jĪ₂X₂, (3.18)

где Х₂= ω₂L_1σ — индуктивное сопротивление рассеяния фазы заторможенного ротора.

Если ротор вращается и s ≠ 0, то уравнение Кирхгофа мож­но представить в виде

Ē_2Кs= Ī₂ R₂+ j Ī₂ X_2Ks, (3.19)

где X_2Ks=ω₁L_2σs = L_2σω₂=X₂— индуктивное сопротивление рассеяния фазы вращающегося ротора.

Поскольку f₂= f₁s, то Х₂является величиной переменной, зависящей от скорости вращения ротора.

Разделив обе части уравнения (3.19) на скольжение, полу­чим после простых преобразований:

Ē_2К= Ī₂R₂+ j Ī₂ Х_2K + Ī₂ R₂(1- s)/s. (3.20)

Выражение имеет физический смысл и означает, что об­мотка вращающегося ротора подобна вторичной обмотке трансформатора, включенной на сопротивление нагрузки, за­висящей от скольжения:

Z_H = R₂(1 -s)/s.

Следовательно, вращающийся ротор с переменной по час­тоте ЭДС е₂ и переменной Х₂ можно привести к неподвижному ротору с ЭДС Ē_2К, изменяющейся с частотой сети f₁ и постоян­ным индуктивным сопротивлением рассеяния Х_2K.

Связь между током Ī₁ в фазе статора и током Ī₂ в фазе ротора асинхронной машины так же аналогична связи токов первичной и вторичной обмоток трансформатора. На самом деле вращающийся поток ротора Ф₂, величина которого зави­сит от числа фаз ротора и тока в фазах, можно представить в виде суммы трех неподвижных в пространстве синусоидаль­ных потоков, сдвинутых по фазе на 120 эл. градусов и направ­ленных по осям А, В, С фазных обмоток статора.

Ф₂ = Ф_2A + Ф_2В+ Ф_2С(3.21)

Потоки взаимоиндукции статора и ротора взаимно непод­вижны, поэтому поток, пронизывающий витки фаз статора мож­но представить в виде алгебраической суммы потока взаимо­индукций статора и ротора:

Ф_A=Ф_1A + Ф_2A,

Ф_B= Ф_1В + Ф_2В, (3.22)

Ф_C= Ф_1C+ Ф_2C.

Как и в трансформаторе эти потоки находятся в противофазе, т. е. потоки ротора являются размагничивающими. По­ток в фазе статора однозначно определяется величиной при­ложенного к фазе напряжения U₁. Следовательно, основной поток фазы статора и основной поток машины Ф во всех режимах машины остаются практически постоянными и рав­ными потоку холостого хода:

Ф = Ф_А + Ф_В+ Ф_С = Ф₀ 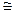const.

Как и в трансформаторе, ток в каждой фазе статора мож­но представить в виде суммы двух составляющих:

Ī₁ = Ī_о+ Ī'₂, (3.23)

где Ī'₂ = I₂К₁ — ток в фазе ротора, приведенный к числу витков и числу фаз обмотки статора. Коэффициент приведения тока:

К_I = (т₁w₁К_об1)(т₁w₁К_о61), (3.24)

где т₂ - число фаз обмотки ротора; для короткозамкнутого ротора т₂ равно числу стержней обмотки.

Составим систему из уравнений (3.17), (3.20) и (3.23):

Ū₁= Ī₁R₁+j Ī₁X₁– Ē₁,

Ē_2К = Ī'₂ R'₂ +j Ī'₂ Х'_2К+ Ī'₂ R'₂ (1 - s)/s, (3.25)

Ī₁= Ī₀ + Ī'₂.

Уравнения (3.25) называются основными уравнениями асинхронного двигателя. В этих уравнениях: R'₂ = R₂K₁K_E — приведенное к обмотке статора активное сопротивление фазы обмотки ротора; Х'_2к = Х_2кК₁К_E — приведенное к обмотке статора индуктивное сопротивление рассеяния фазы затормо­женного ротора. Под приведением понимается замена реаль­ной обмотки ротора с числом фаз т₂, числом витков в фазе w₂и обмоточным коэффициентом K_об2фиктивной обмоткой, име­ющей то же число фаз (т₁), то же число витков в фазе (w₁) и тот же обмоточный коэффициент (K_об1),что и обмотка статора.

Основным уравнениям асинхронного двигателя соответ­ствует векторная диаграмма (рис. 3.10). Векторная диаграмма асинхронной машины мало отличается от векторной диаграм­ма трансформатора, поэтому порядок и необходимые пояснения аналогичны приведенным для трансформатора.

Как и в трансформаторе ток в фазе статора имеет две составляющие: составляющая Ī₀ создает рабочий поток ма­шины и компенсирует потери в стали, составляющая Ī'₂ком­пенсирует размагничивающее действие тока ротора Ī₂на поток машины.

Увеличение нагрузки дви­гателя приводит к уменьше­нию скорости ротора, к увели­чению скольжения, соответ­ственно, ЭДС и тока ротора. Это обуславливает увеличение размагничивающего потока ро­тора Ф₂ и, следовательно, умень­шение рабочего потока Ф. Но уменьшение потока Ф вызывает уменьшение ЭДС Е₁в фазе статора и, следовательно, увели­чение тока Ī₁, что компенсирует в итоге размагничивающее действие потока ротора. Таким образом, всякое увеличение механической мощности на валу машины вызывает увеличение электрической мощности, потребляемой из сети.

Рис. 3.10. Векторная диаграмма асинхронного двигателя